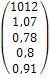5. Розрахувати заробітну плату, яка приходиться на кожне замовлення при виготовленні чоловічих сорочок, якщо відомі дані:
а) затрати робочого часу в годинах на кожному робочому місці (матриця Р);
б) кількість виробів у штуках (матриця Q);
в) погодинна оплата (в у.о.) на кожному робочому місці (матриця С) (табл. 5).
Таблиця 5.
№ з\п |
P |
Q |
C |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
Дано систему алгебраїчних лінійних рівнянь:
, або
у
векторній формі:
=
.
Дослідити на сумісність та знайти розв'язок системи лінійних рівнянь:
1) за допомогою формул Крамера;
2) методом Гаусса;
3) матричним методом (за допомогою оберненої матриці);
4) методом жорданових виключень.
Таблиця 6.
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
-1 |
3 |
1 |
3 |
2 |
3 |
-3 |
1 |
9 |
9 |
5 |
|
2 |
1 |
-1 |
2 |
-1 |
2 |
-3 |
2 |
-1 |
3 |
-1 |
3 |
2 |
|
3 |
3 |
2 |
1 |
2 |
3 |
1 |
2 |
1 |
3 |
5 |
1 |
11 |
|
4 |
2 |
1 |
1 |
1 |
3 |
-2 |
3 |
-2 |
1 |
2 |
1 |
7 |
|
5 |
3 |
1 |
2 |
2 |
-2 |
1 |
1 |
-4 |
3 |
9 |
3 |
1 |
|
6 |
3 |
-2 |
1 |
2 |
1 |
3 |
4 |
-3 |
6 |
-2 |
1 |
-8 |
|
7 |
2 |
2 |
1 |
3 |
-2 |
3 |
1 |
3 |
-2 |
|
2 |
11 |
-6 |
8 |
2 |
2 |
-1 |
3 |
1 |
-3 |
1 |
1 |
5 |
6 |
10 |
-8 |
|
9 |
1 |
1 |
2 |
2 |
-1 |
2 |
4 |
1 |
4 |
-1 |
-4 |
-2 |
|
10 |
1 |
1 |
І |
2 |
-3 |
-1 |
1 |
1 |
-1 |
2 |
5 |
7 |
|
11 |
2 |
2 |
-1 |
3 |
-1 |
2 |
2 |
-1 |
3 |
-7 |
1 |
3 |
|
12 |
1 |
1 |
1 |
2 |
3 |
-1 |
1 |
-1 |
2 |
|
-2 |
1 |
-7 |
13 |
2 |
2 |
3 |
2 |
-3 |
-1 |
3 |
4 |
2 |
1 |
0 |
5 |
|
14 |
2 |
-2 |
3 |
2 |
1 |
5 |
3 |
-4 |
2 |
5 |
10 |
4 |
|
15 |
4 |
2 |
1 |
2 |
2 |
-3 |
3 |
3 |
-5 |
7 |
9 |
1 |
|
16 |
4 |
-2 |
-1 |
2 |
-3 |
2 |
3 |
-5 |
З |
5 |
7 |
5 |
|
17 |
2 |
1 |
-2 |
3 |
1 |
2 |
-1 |
-1 |
2 |
7 |
5 |
-4 |
|
18 |
2 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
2 |
1 |
2 |
4 |
|
19 |
1 |
2 |
3 |
2 |
-1 |
-1 |
1 |
3 |
4 |
5 |
1 |
6 |
|
20 |
3 |
2 |
1 |
1 |
1 |
-1 |
4 |
-1 |
5 |
5 |
0 |
3 |
|
21 |
2 |
4 |
-5 |
3 |
3 |
-2 |
2 |
-1 |
-2 |
-7 |
-2 |
1 |
|
22 |
2 |
5 |
4 |
3 |
-2 |
-3 |
1 |
1 |
-2 |
1 |
2 |
-2 |
|
23 |
3 |
-1 |
2 |
2 |
3 |
-1 |
1 |
-2 |
3 |
0 |
6 |
-4 |
|
24 |
3 |
4 |
6 |
2 |
3 |
5 |
1 |
_2 |
-4 |
1 |
0 |
3 |
|
25 |
2 |
-4 |
5 |
3 |
-2 |
3 |
4 |
5 |
-2 |
3 |
4 |
7 |
|
