
- •1. Елементи теорії надійності
- •Експоненціальний та інші розподіли ймовірності безвідмовної роботи
- •Контрольні питання
- •1.3. Методи забезпечення надійності
- •Контрольні питання
- •1.4. Резервування апаратури
- •Структура буде залишатися працездатною в таких ситуаціях:
- •При порівнянні формул (1.12) з (1.14) та (1.13) з (1.15) можна зробити очевидний висновок: при надійність структур з во з пам’яттю вища, ніж у мажоритарних структур.
- •1.5. Інформаційна надлишковість як універсальний засіб контролю
- •Контрольні питання
- •Контрольні питання
- •2.2. Завадозахищене кодування Фундаментальним поняттям в захисті від завад є інформаційна надлишковість. За к. Шеноном інформаційна надлишковість оцінюється як
- •Контрольні питання
- •2.3. Кодові методи функціонального контролю
- •Контрольні питання
- •2.4. Тестовий контроль
- •Контрольні питання
- •2.5. Імовірнісні та сигнатурні методи контролю
- •Література
Контрольні питання
У чому полягає різниця між функціональним та тестовим контролем?
Що є визначальним при виборі методу функціонального контролю?
Що таке “двопровідна логіка”?
У чому полягає метод “зворотної помилки”? У яких випадках цей метод не може бути застосованим?
Із яких міркувань формується множина помилок, які необхідно виявляти при функціональному контролі?
2.2. Завадозахищене кодування Фундаментальним поняттям в захисті від завад є інформаційна надлишковість. За к. Шеноном інформаційна надлишковість оцінюється як
![]() , (2.1)
, (2.1)
де
![]() ; (2.2)
; (2.2)
– розрядність слів при двійковому кодуванні.
–
максимальна
ентропія, яка має місце, коли всі
![]() (
(![]() )
однакові, тобто
)
однакові, тобто
![]() і
ентропія може бути визначена за формулою
Хартлі
і
ентропія може бути визначена за формулою
Хартлі
![]() (2.3)
(2.3)
При
будь якому відхиленні
від рівномірного
розподілу можна говорити про інформаційну
надлишковість, і
![]() .
.
До речі, інформаційну надлишковість іноді зручніше вимірювати просто як
![]() (2.4)
(2.4)
Нас
буде цікавити випадок, коли деяка частина
-розрядних
слів із загальної кількості
![]() не використовується. Позначимо кількість
таких слів через
не використовується. Позначимо кількість
таких слів через
![]() і будемо називати їх забороненими. Це
означає, що деякі ймовірності
і будемо називати їх забороненими. Це
означає, що деякі ймовірності
![]() і
і
![]() .
Підмножина слів, кількість яких
.
Підмножина слів, кількість яких
![]() ,
є дозволеними словами і використовуються
джерелом інформації для кодування
повідомлень.
,
є дозволеними словами і використовуються
джерелом інформації для кодування
повідомлень.
Очевидно,
![]() .
.
Очевидно також, що помилка в повідомленні може бути виявлена тоді і тільки тоді, коли вона перетворює дозволене слово в заборонене.
Для кожного дозволеного слова таких різних помилок може бути рівно , а максимальна кількість всіх можливих помилок при заданому способі двійкового кодування
![]() ,
,
де 1 записана в рахунок випадку, коли помилок немає. Відносну кількість (“долю”) помилок, яку можна виявити при заданому способі кодування, обчислимо як
![]() .
(2.5)
.
(2.5)
Обчислимо
![]() для таких випадків.
для таких випадків.
Код із однією перевіркою на парність.
;
![]() (дозволені слова мають парну кількість
одиниць – їх рівно половина).
(дозволені слова мають парну кількість
одиниць – їх рівно половина).
![]() (50%)
(50%)
Код, що має два додаткових розрядів (код із контролем по модулю 3)
![]() (75%).
(75%).
3. Код із “повторенням“. Кожне слово передається джерелом двічі. Тоді
![]() (100%)
(100%)
З цих прикладів бачимо, що здатність коду до виявлення помилок зростає дуже швидко із зростанням надлишковості. Зауважимо також, що формула (2.5) є універсальною в тому розумінні, що оцінка здатності до виявлення помилок не залежить від способу кодування інформації.
У класичній теорії кодування застосовується дещо інший підхід. Він базується на визначенні кодової відстані та понятті кратності помилки . При двійковому кодуванні:
– кодова
відстань
![]() d
d![]() між двома словами – це кількість
розрядів, якими відрізняється одне
слово від другого;
між двома словами – це кількість
розрядів, якими відрізняється одне
слово від другого;
– кратність помилки .t – це кількість розрядів, які спотворені помилкою;
– вектор помилки E=(e1,e2,….,en) .– це двійкова комбінація, яка містить 1 в тих розрядах слова, які спотворені.
Таким чином, кратність помилки – це “вага” вектора помилки – кількість одиниць в ньому.
Легко довести, що мінімальна кодова відстань для виявлення помилок кратності і менше повинна бути
![]() (2.6)
(2.6)
При виконанні (2.6) жодна помилка кратності і менше не зможе перетворити одне дозволене слово в інше також дозволене слово).
Очевидно,
формули (2.5) і (2.6) у конкретних випадках
мають бути еквівалентні. Спробуємо це
показати. Візьмемо знову код із однією
перевіркою на парність.
Додавши
один розряд таким чином, щоб кількість
одиниць у слові стала парною, ми
“розносимо” слова на
![]() (до
цього було
(до
цього було
![]() ).
Зразу ж можна стверджувати, що будь-яка
однократна помилка у цьому випадку буде
виявлятися, бо вона перетворює слово
із парною кількістю одиниць у слово із
непарною кількістю. А які інші помилки
будуть виявлятися? Очевидно, всі ті, для
яких
непарне. А всього таких помилок буде
приблизно половина (50%). В інших випадках
потрібен детальний аналіз конкретних
помилок, які виявляються і які не
виявляються.
).
Зразу ж можна стверджувати, що будь-яка
однократна помилка у цьому випадку буде
виявлятися, бо вона перетворює слово
із парною кількістю одиниць у слово із
непарною кількістю. А які інші помилки
будуть виявлятися? Очевидно, всі ті, для
яких
непарне. А всього таких помилок буде
приблизно половина (50%). В інших випадках
потрібен детальний аналіз конкретних
помилок, які виявляються і які не
виявляються.
А тепер про більш складний випадок – виправлення помилок. Яка для цього потрібна надлишковість? І найголовніше, що потрібно для того, щоб помилку можна було не тільки виявити але й виправити? Очевидно, попередня умова,виконання якої необхідне для виявлення помилок, залишається справедливою і для їх виправлення: помилка повинна перетворювати дозволене слово в заборонене. Але цього не досить. Якщо два чи більше дозволених слова можуть переходити в одне заборонене, то, отримавши це слово замість дозволеного (без помилок), у отримувача не буде підстав, щоб надати перевагу будь-якій із гіпотез щодо того, яке саме дозволене слово було спотворено завадою. Що ж потрібно для того, щоб можна було таку первагу віддати? Очевидно, для надання такої переваги ймовірності помилок повинні бути суттєво різними. Тоді, отримавши заборонене слово, будемо мати підстави віддати перевагу тій помилці, яка має найбільшу ймовірність. Але де взяти ці ймовірності? В реальних випадках вони не можуть вважатися відомими.
В теорії завадостійкого кодування вважається (і це може бути обґрунтовано теорією ймовірностей),що для незалежних помилок ймовірність виникнення помилки дуже швидко зменшується із зростанням її кратності, тобто найбільш ймовірні однократні помилки, менш ймовірні 2-кратні помилки і так далі.
У будь-якому випадку множина можливих помилок завжди має бути обмежена або конкретною кратністю, або конкретним переліком. Якщо таке обмеження виконано, (а це обов’язково треба зробити), то достатню умову для можливості виправлення помилок можна сформулювати так: кожна з помилок, яка має бути виправлена, повинна переводити кожне із дозволених слів не більше, ніж в одне заборонене слово.
Таким
чином, кожному дозволеному слову треба
мати можливість співставити не менше,
ніж
![]() заборонених слів, звідси безпосередньо
витікає, що
заборонених слів, звідси безпосередньо
витікає, що
![]() ,
,
або
![]() ,
звідки
,
звідки
![]() (2.7)
(2.7)
Для виправлення помилок певної кратності (частковий випадок) корегуючу здатність можна визначити через мінімальну кодову відстань
![]() (2.8).
(2.8).
Групові коди. Із попереднього
матеріалу може скластися враження, що
знаючи співвідношення (2.6) та (2.8), легко
побудувати будь-який код. Наприклад,
для цього, здавалось би, досить “рознести”
дозволені слова на відповідну мінімальну
відстань, і задачу можна вважати
розв’язаною. Але це лише на перший
погляд. Дійсно, коли треба знайти,
наприклад, тільки кілька сотень дозволених
слів (![]() ),
то за допомогою комп’ютера це можна
зробити, мабуть, за кілька хвилин. В
результаті будемо мати таблицю дозволених
слів, яку можна використати при декодуванні
(виявленню або виправленню помилок). А
що коли
),
то за допомогою комп’ютера це можна
зробити, мабуть, за кілька хвилин. В
результаті будемо мати таблицю дозволених
слів, яку можна використати при декодуванні
(виявленню або виправленню помилок). А
що коли
![]() або ще більше? Де зберігати таку таблицю,
якщо її навіть вдасться побудувати? (На
це потрібно витратити далеко не хвилини
і навіть не години комп’ютерного часу,
бо задача має комбінаторний характер).
або ще більше? Де зберігати таку таблицю,
якщо її навіть вдасться побудувати? (На
це потрібно витратити далеко не хвилини
і навіть не години комп’ютерного часу,
бо задача має комбінаторний характер).
Головна мета класичної теорії кодування полягає у створенні конструктивних процедур кодування і декодування, які мають прості апаратні або програмні реалізації. Теорія кодування вивчає головним чином так звані групові коди. Ця назва походить від поняття група з вищої алгебри.
Група – це замкнена відносно групової операції сукупність об’єктів. Група обов’язково містить також елемент, який називають одиничним або нульовим в залежності від того, яка використовується групова операція. Поняття замкненості полягає в тому, що застосування групової операції до двох чи більше елементів групи дає в результаті також елемент групи, а групова операція між будь-яким елементом групи і одиничним (нульовим) елементом дає в результаті сам елемент.
Все це – визначення на абстрактному рівні, і, мабуть, не зовсім зрозуміло, про що йде мова. Наведемо прості приклади, які зроблять ці визначення прозорими.
Всі
дійсні числа – група відносно операції
додавання (![]() )
із нульовим елементом 0.
Складаючи дійсні числа, ми завжди
отримуємо теж дійсні числа (замкненість),
а додавши 0
до будь-якого числа, ми отримуємо теж
саме число. Відносно операції множення
(
)
із нульовим елементом 0.
Складаючи дійсні числа, ми завжди
отримуємо теж дійсні числа (замкненість),
а додавши 0
до будь-якого числа, ми отримуємо теж
саме число. Відносно операції множення
(![]() )
з одиничним елементом 1
теж отримаємо замкнену групу. Інший
приклад: числа, які без остачі діляться
на 3.
Складаючи або перемножуючи такі числа,
ми отримуємо числа, які без остачі
діляться на 3.
Можна навести і інші численні приклади.
)
з одиничним елементом 1
теж отримаємо замкнену групу. Інший
приклад: числа, які без остачі діляться
на 3.
Складаючи або перемножуючи такі числа,
ми отримуємо числа, які без остачі
діляться на 3.
Можна навести і інші численні приклади.
В
теорії кодування двійкові
-розрядні
слова
![]() – це група відносно операції порозрядного
додавання по модулю 2
(
),
а нульовий елемент – кодове слово
– це група відносно операції порозрядного
додавання по модулю 2
(
),
а нульовий елемент – кодове слово
![]() .
.
Саме по собі таке визначення поки нічого не дає – проблема компактного представлення множини кодових слів зберігається. Але з математики відомо, що група може бути представлена своїм базисом. Базис – це мінімальна сукупність незалежних елементів, застосовуючи до яких групову операцію (до різних сполучень елементів базису), можна відтворити всю групу.
Наприклад,
Базис:
![]() ;
;![]() ;
;![]() .
.
Похідгні:![]() ;
;![]() ;
;![]() ;
;![]()
Повна сукупність:000,100, 010, 001, 110, 101, 011, 111.
Можна сказати, що базис “породжує” повну сукупність елементів групи плюс нульовий елемент, який повинен бути в групі за визначенням. Базис – компакт групи.
Наведений приклад ілюструє лише саму ідею представлення групи своїм базисом. Звичайно, щоб задати всі 3-розрядні комбінації, зовсім не потрібно вводити нові спеціальні поняття.
Візьмемо інший приклад:
100110 100110
0 10011 010011
10011 010011
001101 001101
110101
Базис 101011
011110
111000
000000
Повна сукупність
(Звернемо увагу: ми задали 8 слів за допомогою трьох).
Базис зручно (у цьому переконаємося у подальшому) представляти відповідною матрицею. У нашому випадку
![]() (2.9)
(2.9)
Таку
матрицю називають породжуючою
і майже завжди позначають символом
![]() .
.
У більшості випадків процедура кодування
полягає у доповненні вихідного (исходного
– рос.) слова деякою кількістю додаткових
(надлишкових або перевірочних) символів
(розрядів). Будемо (як ми вже домовились)
позначати кількість вихідних розрядів
через
,
а кількість додаткових – через (![]() ),
тобто
),
тобто
 розрядів
розрядів
розрядів
розрядів
![]()
![]()
Зауважимо, що значення перших розрядів кодування повинні зберігатися. Це так звані систематичні (розділимі) коди.
А з цього безпосередньо витікає, що в породжуючій матриці перші стовпців повинні утворювати одиничну квадратну матрицю рангу . Тільки у цьому випадку перші розрядів кодової комбінації зможуть приймати довільні значення. Виконання цієї вимоги є необхідним для того, щоб не накладати будь-яких обмежень на інформацію, що підлягає кодуванню. Таким чином,
![]() ,
(2.10)
,
(2.10)
де
![]() -
одинична квадратна матриця рангу
;
-
одинична квадратна матриця рангу
;
![]() -
матриця розмірності
-
матриця розмірності
![]() .
.
Нагадаю, що
задає множину кодових слів, а кожен
рядок
– це теж кодове слово. Тому всі вимоги
до множини кодових слів повинні
виконуватися і для рядків
.
Зокрема, якщо кодові слова повинні бути
рознесені на відстань
![]() одне від одного, то ця ж сама вимога
повинна виконуватись і для рядків
.
Для нашого прикладу можна переконатися,
що як для
,
так і для повної множини кодових слів,
породжених
,
одне від одного, то ця ж сама вимога
повинна виконуватись і для рядків
.
Для нашого прикладу можна переконатися,
що як для
,
так і для повної множини кодових слів,
породжених
,
![]() .
(Згадаємо, що такий код спроможний
корегувати всі однократні помилки).
Тобто, виконавши певні вимоги до
,
ми забезпечуємо задані властивості для
усієї множини кодових слів.
.
(Згадаємо, що такий код спроможний
корегувати всі однократні помилки).
Тобто, виконавши певні вимоги до
,
ми забезпечуємо задані властивості для
усієї множини кодових слів.
З точки зору математики процедура
кодування еквівалентна матричному
множенню довільного
-
розрядного слова
![]() на породжуючи матрицю
.
Результатом такого множення буде добуток
у вигляді
-розрядного
слова
на породжуючи матрицю
.
Результатом такого множення буде добуток
у вигляді
-розрядного
слова
![]() .
Причому,
.
Причому,
![]() та
та
![]() треба розглядати як вектор-рядки, а
операції множення і додавання виконуються
за правилами алгебри логіки:
треба розглядати як вектор-рядки, а
операції множення і додавання виконуються
за правилами алгебри логіки:
Проаналізуємо, що відбудеться при такому множенні:
![]()
![]()
нагадаю, що -й розряд добутку – це скалярний добуток - го розряду та -го стовпця . Тобто
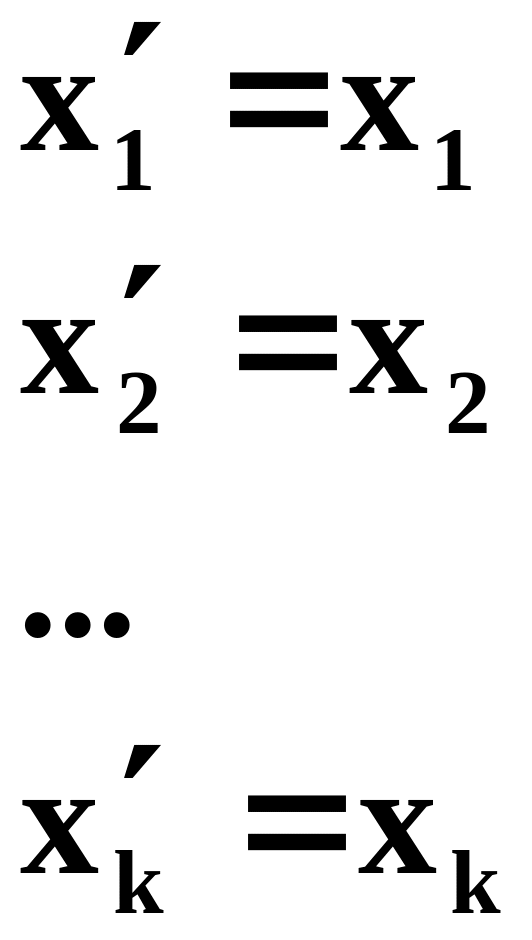
![]()
Останні
![]() рівнянь називаються рівняннями кодування.
Вони, по суті, в явній формі визначають
залежність значень додаткових розрядів
від значень інформаційних.
рівнянь називаються рівняннями кодування.
Вони, по суті, в явній формі визначають
залежність значень додаткових розрядів
від значень інформаційних.
В узагальненому вигляді кожне рівняння кодування можна записати як
![]() ,
,
![]() .
.
Це рівняння можна переписати так:
![]() ,
(2.11)
,
(2.11)
Треба підкреслити, що ми лише переписали рівняння, врахувавши особливості функції . Зокрема, ми маємо право переносити будь-який доданок з лівої частини в праву і навпаки без зміни знаку, бо від’ємні доданки не мають змісту.
До цього моменту ми ніяк не враховували помилки, і рівняння (2.11) виконується, коли помилок немає. А якщо вони виникнуть, то може вже і не виконуватися, тобто
,
![]()
д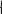 е
е
![]() =
0, якщо помилки немає або вона не
виявляється, та ri=1,
коли помилка є.
=
0, якщо помилки немає або вона не
виявляється, та ri=1,
коли помилка є.
Рівняння (2.12) називаються рівняннями перевірки, а - результатом -ї перевірки.
Сукупність результатів перевірки називається перевірочною послідовністю або синдромом
![]() .
.
З точки зору математики обчислення
синдрому може бути записане як результат
матричного множення
-розрядного
слова на деяку матрицю
![]() ,
яку називають перевірочною. Спосіб її
утворення можна записати так:
,
яку називають перевірочною. Спосіб її
утворення можна записати так:
![]() ;
; ![]() ,
,
де
![]() – одинична квадратна матриця рангу
,
– одинична квадратна матриця рангу
,
![]() – транспонована матриця
– транспонована матриця
![]() ,
тобто матриця, отримана із
заміною рядків на стовпці:
,
тобто матриця, отримана із
заміною рядків на стовпці:
![]() ;
;![]() Таким
чином, перевірочна матриця
має
рядків і
стовпців,
а кожен рядок відповідає одній перевірці.
З цього витікає, що результатом множення
-розрядного
слова на
є саме синдром, тобто
Таким
чином, перевірочна матриця
має
рядків і
стовпців,
а кожен рядок відповідає одній перевірці.
З цього витікає, що результатом множення
-розрядного
слова на
є саме синдром, тобто
![]()
А тепер повернемось до власне помилок. А саме, яка відповідність між помилками та синдромами. Кодову комбінацію, яка спотворена помилкою, можна записати так:
![]() ,
,
де
![]() -
комбінація без помилок, тобто та, яку
передавало джерело інформації. Синдром,
що відповідає
-
комбінація без помилок, тобто та, яку
передавало джерело інформації. Синдром,
що відповідає
![]()
![]()
Але
за визначенням
![]() та
та
![]() ,
(2.13)
,
(2.13)
тобто
синдром для певної конкретної помилки
![]() можна отримати, помноживши вектор
помилки
на перевірочну матрицю.
можна отримати, помноживши вектор
помилки
на перевірочну матрицю.
Ми вже знаємо, що в більшості випадків можна вважати, що найбільш ймовірними є однократні помилки. Тому, насамперед потрібно з’ясувати, який вигляд має відповідність між векторами однократних помилок і синдромами. Знайдемо синдроми, як відповідають однократним помилкам в -розрядному кодовому слові.
![]()
Оскільки – вектор однократної помилки, то серед його компонент є тільки одна одиниця. З цього витікає, що синдром помилки в -му розряді кодового слова в точності співпадає з -м стовпцем матриці . Іншими словами, стовпці матриці – це синдроми однократних помилок. Тому
![]() ,
,
де
лише
![]() .
.
Тепер вже можна сформувати вимоги до перевірочної матриці групового коду для виявлення і виправлення помилок.
Виявлення помилок.
Помилка виявляється кодом, якщо
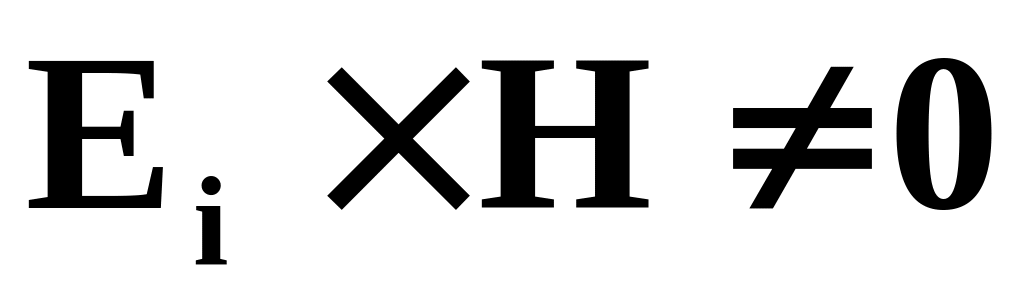 .
.Перевірочна матриця коду, що виявляє всі однократні помилки, повинна мати ненульових стовпців.
У найпростішому випадку
![]() ,
і, відповідно,
,
і, відповідно,
![]()
– це код з однією перевіркою на парність, що має один додатковий символ
![]() .
.
Рівняння перевірки
![]() .
.
Виправлення (корекція) помилок.
Очевидно,
якщо код повинен виправляти сукупність
помилок
![]() ,
то всі відповідні цим помилкам синдроми
повинні бути різними, тобто відповідність
,
то всі відповідні цим помилкам синдроми
повинні бути різними, тобто відповідність
![]() має бути взаємно однозначною. Тільки в
цьому випадку ми зможемо за значенням
синдрому знайти відповідний йому вектор
помилки і виправити помилку. З цього
зокрема витікає, що перевірочна матриця
коду, який виправляє всі однократні
помилки, повинна мати n
різних
ненульових стовпців. Зокрема матриця,
в якій стовпці пробігають всі ненульові
значення
-розрядних
чисел
має бути взаємно однозначною. Тільки в
цьому випадку ми зможемо за значенням
синдрому знайти відповідний йому вектор
помилки і виправити помилку. З цього
зокрема витікає, що перевірочна матриця
коду, який виправляє всі однократні
помилки, повинна мати n
різних
ненульових стовпців. Зокрема матриця,
в якій стовпці пробігають всі ненульові
значення
-розрядних
чисел
![]() (2.14)
(2.14)
може бути використана як перевірочна коду, який виправляє всі однократні помилки. Така матриця відрізняється від канонічної форми
![]() (2.15)
(2.15)
лише розташуванням стовпців. Якщо стовпці, які містять по одній одиниці, перенести праворуч і сформувати з них одиничну матрицю, то ми отримаємо саме форму (2.14). Слід зазначити, що така процедура еквівалентна лише перенумерації позицій символів і не є принциповою з точки зору властивостей коду.
Форма матриці (2.14) є цікавою з іншого погляду. По-перше, саме у такому вигляді були запропоновані Хемінгом перші коди із корекцією помилок. По-друге, при використанні такої матриці синдром безпосередньо у двійковому вигляді вказує номер розряду, який спотворено:
![]()
![]()
100...00 00...01
010...00 00...10
001...00 00...11
... ...
000...01 11...11
У кодах Хемінга додаткові (перевірочні) розряди займають 1, 2, 8,...,2n-k позиції. З точки зору матричного представлення це не дуже зручно, але з технічної – не викликає жодних додаткових проблем.
Хемінгом були запропоновані (1948р.) три класи кодів.
Уже розглянутий нами код з однією перевіркою на парність. Для нього і він виявляє всі помилки непарної кратності. Для нього
 .
.Коди з виправленням однократних помилок з . Це ряд кодів, для яких
![]() (2.16)
(2.16)
Наприклад, код з
![]() і
і
![]()
![]()
1234567
Із перевірочної матриці можна викреслити деяку кількість стовпців і це не зменшить корегуючої здатності кода. Головне – не зменшувати кількість перевірочних розрядів. Такі коди (отримані шляхом викреслення деякої кількості стовпців із повної матриці) називають укороченими.
Ще один клас кодів Хемінга з
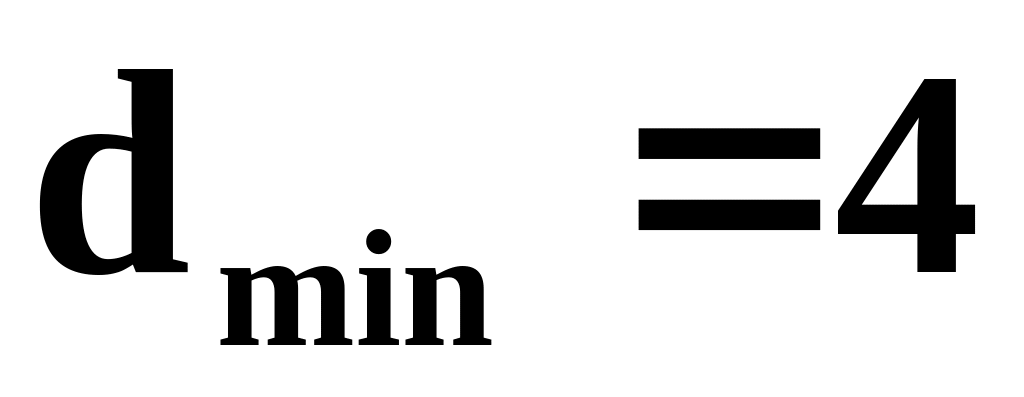 .
Ці коди дозволяють виявляти помилки
кратності
.
Ці коди дозволяють виявляти помилки
кратності
 ,
або виправляти помилки кратності
,
або виправляти помилки кратності
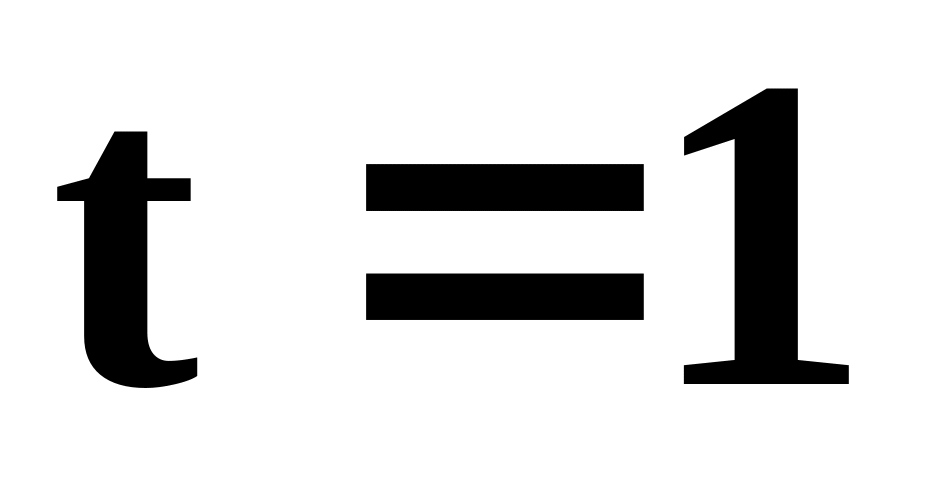 та
виявляти помилки кратності
та
виявляти помилки кратності
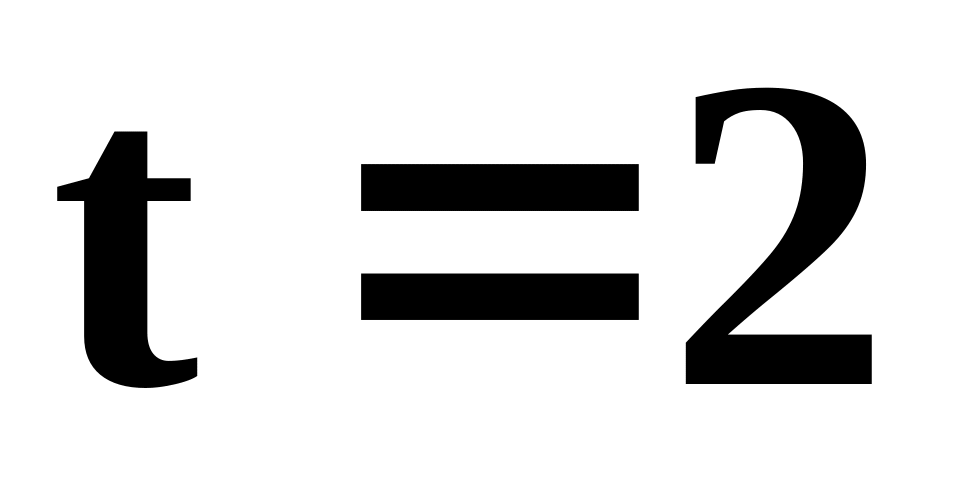 .
Саме у цьому варіанті такі коди найчастіше
і використовують.
.
Саме у цьому варіанті такі коди найчастіше
і використовують.
Щоб отримати код з , досить перевірочну матрицю коду з доповнити ще одним рядком з одиниць:
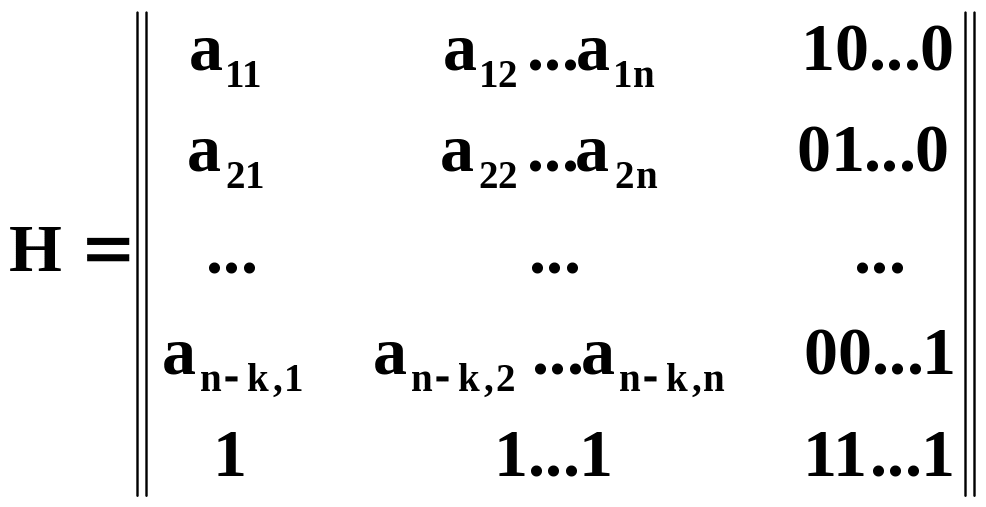
Цьому додатковому
рядку відповідає ще один
![]() -ий
додатковий розряд і ще одне рівняння
перевірки
-ий
додатковий розряд і ще одне рівняння
перевірки
![]()
Таким чином, при декодуванні ми отримуємо результатів перевірки
![]() та
та
![]() .
.
Другий етап декодування коду базується на аналізі результатів перевірки. Вони можуть бути такими:
а)
![]() ;
;
![]() –
помилок немає;
–
помилок немає;
б)
![]() ;
–
однократна помилка, яка може бути
виправлена на основі відповідності
;
–
однократна помилка, яка може бути
виправлена на основі відповідності
![]() ;
;
в) ; r0 = 0 – 2-кратна помилка, яка лише виявляється, але не може бути виправлена.
Таким чином, ми маємо
універсальний метод побудови кодів з
![]() ,
які, відповідно, виявляють однократні
помилки, виправляють однократні та
виявляють 2-кратні.
,
які, відповідно, виявляють однократні
помилки, виправляють однократні та
виявляють 2-кратні.
Для інших випадків не існує універсальних методів, тобто придатних для довільних значень або , побудови кодів. В узагальненому вигляді задача побудови коду формулюється так.
Задана сукупність
векторів помилок
![]() .
Необхідно знайти таку перевірочну
матрицю
,
для якої всі добутки
.
Необхідно знайти таку перевірочну
матрицю
,
для якої всі добутки
![]() для випадку виявлення заданої сукупності
помилок та додатково у випадку їх
виправлення всі синдроми повинні бути
різними, тобто
для випадку виявлення заданої сукупності
помилок та додатково у випадку їх
виправлення всі синдроми повинні бути
різними, тобто
![]() для
всіх
для
всіх
![]() .
.
В принципі не існує
іншого алгоритму, крім прямого перебору,
побудови кодів, що корегують (виявляють
або виправляють) довільну сукупність
помилок. При виконанні такого перебору
може виявитися корисною така властивість:
якщо вектору помилки
відповідає
синдром
![]() ,
а
,
а
![]() ,
то вектору помилки
,
то вектору помилки
![]() (2.17)
(2.17)
(ця властивість є наслідком лінійності всіх операцій, які застосовуються у теорії кодування).
Задача аналізу кодів, що виправляють помилки, досить складна тому, що потрібно аналізувати не окремі вектори помилки, а їх повну сукупність: всі синдроми, що відповідають такій сукупності, повинні бути різними. Як цього досягти для однократних помилок, ми вже розглянули. Для деяких інших сукупностей – розглянемо в наступному розділі в рамках циклічних кодів.
Циклічні коди. Насамперед зауважимо, що циклічні коди є підкласом групових кодів, тобто циклічні коди теж групові, але мають свою специфіку головним чином щодо математичного апарату та символіки, які використовуються для їх побудови та аналізу. В терміналах абстрактної алгебри циклічний код – це кільце, тобто така замкнена сукупність елементів, для яких задані дві операції та обернені до них. Зокрема, в нашому випадку це порозрядне додавання (обернена операція співпадає із самою операцією) та множення (зворотна – ділення). Самі елементи – двійкові -розрядні комбінації – записуються як поліноми. Правило, за яким встановлюється відповідність, можна пояснити прикладом:
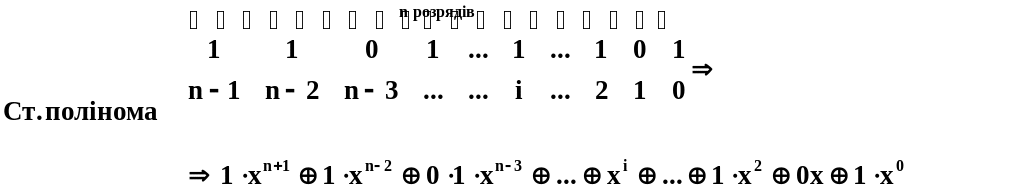
Більш компактно цей поліном можна записати так:
![]()
Такі поліноми можна додавати, множити і ділити за звичайними правилами з урахуванням специфіки операції суми по модулю 2, а саме
![]() ;
; ![]()
Наприклад,
а)
![]()
б)![]()
в)
![]()
Можна дати таке (спрощене) визначення циклічного коду.
Циклічний код утворює
множина дозволених кодових комбінацій,
відповідні яким поліноми без остачі
діляться на деякий поліном
![]() ,
який називають породжуючим. (Аналогія:
множина чисел, які без остачі діляться
на деяке число
,
який називають породжуючим. (Аналогія:
множина чисел, які без остачі діляться
на деяке число
![]() Наприклад, всі числа кратні 2 (парні
числа), або 3 чи іншому числу).
Наприклад, всі числа кратні 2 (парні
числа), або 3 чи іншому числу).
Існує два способи утворення циклічного коду, точніше, дозволених кодових комбінацій.
Множенням довільної -розрядної комбінації у вигляді відповідного їй полінома
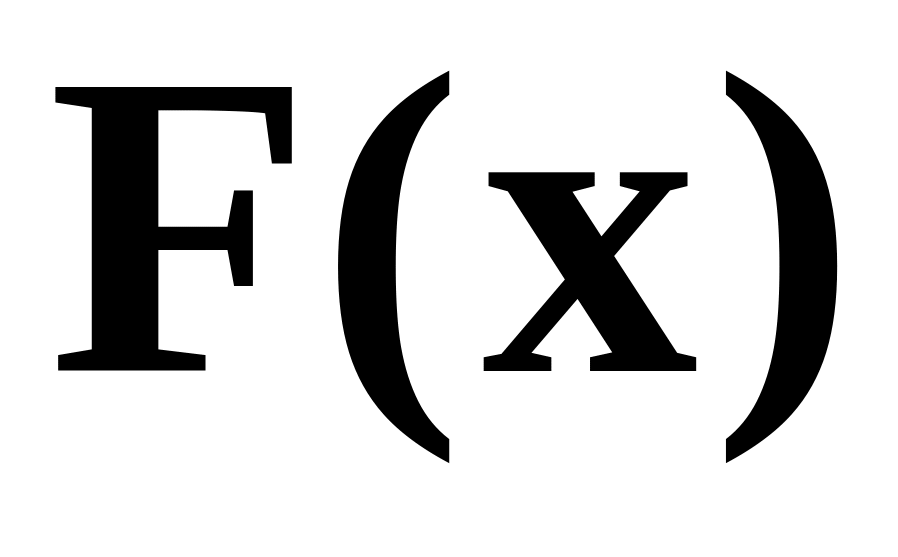 ступені
ступені
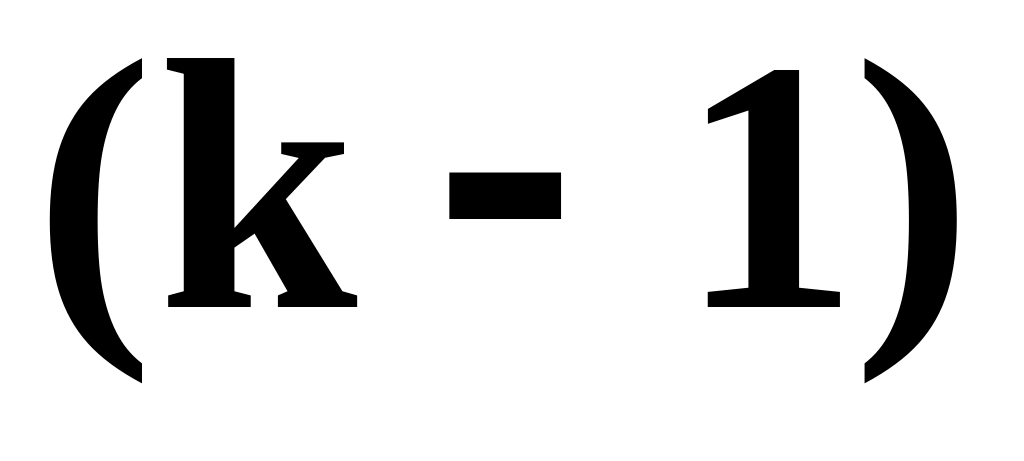 на породжуючий поліном
.
У цьому випадку кодове слово може бути
представлене як
на породжуючий поліном
.
У цьому випадку кодове слово може бути
представлене як
![]()
і, очевидно, воно
завжди без остачі ділиться на
![]() .
.
Такий спосіб з математичної точки зору є найбільш простим і прозорим, але на практиці застосовується дуже рідко. Причина полягає в тому, що в цьому випадку ми отримуємо несистематичний (нерозділимий) код – інформаційна частина у кодовій комбінації не зберігається (в результаті множення вона “змішується” з ). Це суттєво ускладнює процедуру декодування при наявності помилок.
Дописуванням до з боку молодших розрядів остачі
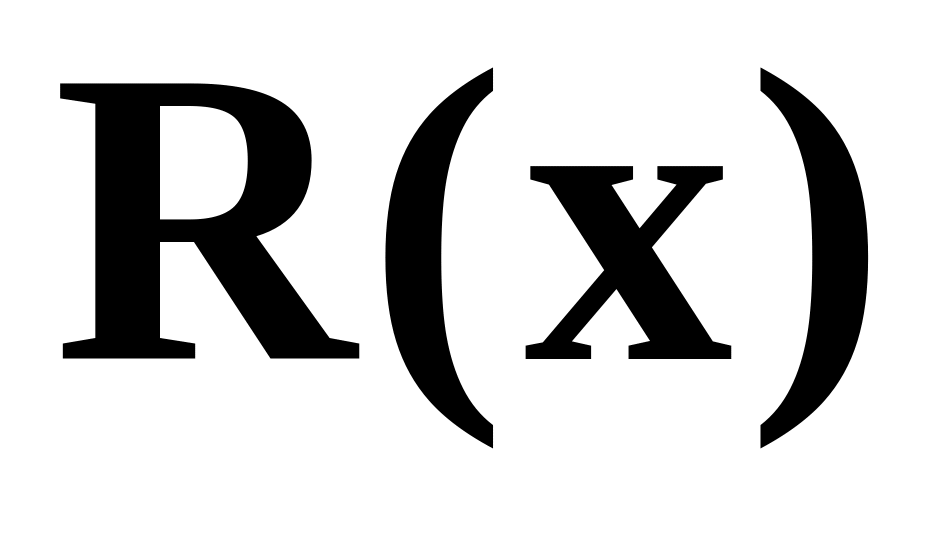 від ділення
від ділення
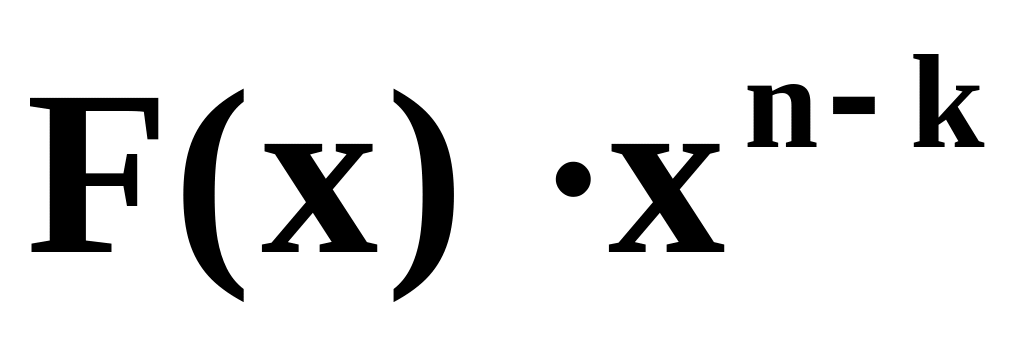 на породжуючий поліном
.
(Зазначимо, що множення на
на породжуючий поліном
.
(Зазначимо, що множення на
 означає просте дописування до
нулів.) Формально це можна записати так
означає просте дописування до
нулів.) Формально це можна записати так
![]() .
.
Неважко переконати,
що отриманий таким чином поліном завжди
буде без остачі ділитися на
![]() .
.
Як підкреслювалось
на самому початку, циклічні коди є
підкласом групових кодів, тобто будь
який циклічний код може бути заданий
також відповідно породжуючою матрицею
![]() .
Для цього досить знайти остачі для
перших
.
Для цього досить знайти остачі для
перших
![]() рядків
одиничної матриці
рядків
одиничної матриці
![]()
![]()
Не
будемо забувати, що рядки матриці
– це насамперед кодові слова в вони
можуть бути утворені за звичайними
правилами. Утворимо їх для прикладу
конкретного кода з
![]() і
і
![]() .
.
Рядки одиничної матриці і відповідні операції:
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
Таким чином, породжую чому поліному для кода з інформаційними розрядами відповідає породжуюча матриця
![]() .
.
Циклічний код з і груповий код з еквівалентні. Крім того, як неважко переконатися, обчислення остачі еквівалентно обчисленню синдрому в групових кодах. Зауважимо також, що відповідність між груповими і циклічними кодами не є взаємною: будь-якому циклічному коду можна знайти еквівалентний груповий код, але не навпаки. Клас групових кодів значно ширший, ніж клас циклічних кодів.
Основні циклічні коди. На практиці саме циклічні коди використовуються найчастіше. Це пояснюється їх простою схемною реалізацією на регістрах зсуву із зворотними зв’язками та простим математичним апаратом, за допомогою якого можна описати циклічні коди та проаналізувати їх корегуючу здатність.
Для
побудови циклічних кодів найчастіше
використовуються так звані неприводимі
поліноми (аналог – прості числа). Із
теорії кодування відомо, що далеко не
всі неприводимі поліноми придатні для
побудови ефективних кодів. Так, для
отримання максимального числа різних
остач при декодуванні породжуючий
поліном
повинен
бути дільником
![]() .
Таблиці неприводимих дільників для
різних значень
.
Таблиці неприводимих дільників для
різних значень
![]() наводяться у більшості книжок з теорії
кодування. Не заглиблюючись в дебрі
теорії, приймемо цю вимогу на віру і
розглянемо деякі конкретні коди.
наводяться у більшості книжок з теорії
кодування. Не заглиблюючись в дебрі
теорії, приймемо цю вимогу на віру і
розглянемо деякі конкретні коди.
Код з
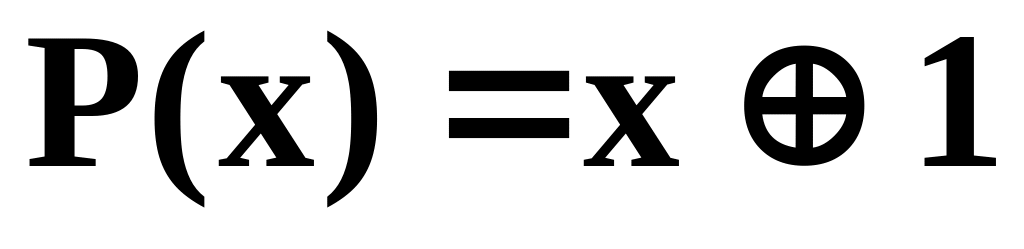 ми вже фактично розглянули. Цей код
забезпечує
і дозволяє виявляти всі однократні
помилки, а також всі помилки непарної
кратності. Це легко довести, аналізуючи
подільність полінома, що відповідає
вектору помилки
ми вже фактично розглянули. Цей код
забезпечує
і дозволяє виявляти всі однократні
помилки, а також всі помилки непарної
кратності. Це легко довести, аналізуючи
подільність полінома, що відповідає
вектору помилки
 (кількість доданків непарна), на
.
(кількість доданків непарна), на
.
2. Код
з
.
Цей поліном неприводимий і є дільником
![]() ,
тому існує код з
та
.
Код з такими параметрами дає
,
тому він спроможний виправляти однократні
помилки або виявляти двократні. Такі
самі характеристики має код з
,
тому існує код з
та
.
Код з такими параметрами дає
,
тому він спроможний виправляти однократні
помилки або виявляти двократні. Такі
самі характеристики має код з
![]() .
Із таблиць можемо знайти інші поліноми
для інших значень
та
.
Наприклад,
.
Із таблиць можемо знайти інші поліноми
для інших значень
та
.
Наприклад,

Всі ці коди оптимальні (довершені) і є аналогами уже розглянутих нами кодів Хемінга. В таблиці наведено лише по одному поліному для кожного значення та (насправді може бути по кілька еквівалентних варіантів).
Код з
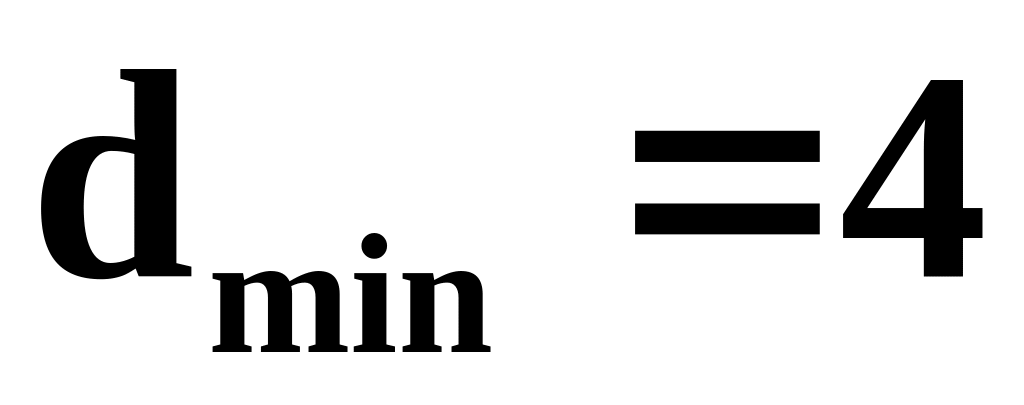 для виправлення однократних і виявлення
двократних помилок. Такі коди отримують
із попередніх домноженням
для виправлення однократних і виявлення
двократних помилок. Такі коди отримують
із попередніх домноженням
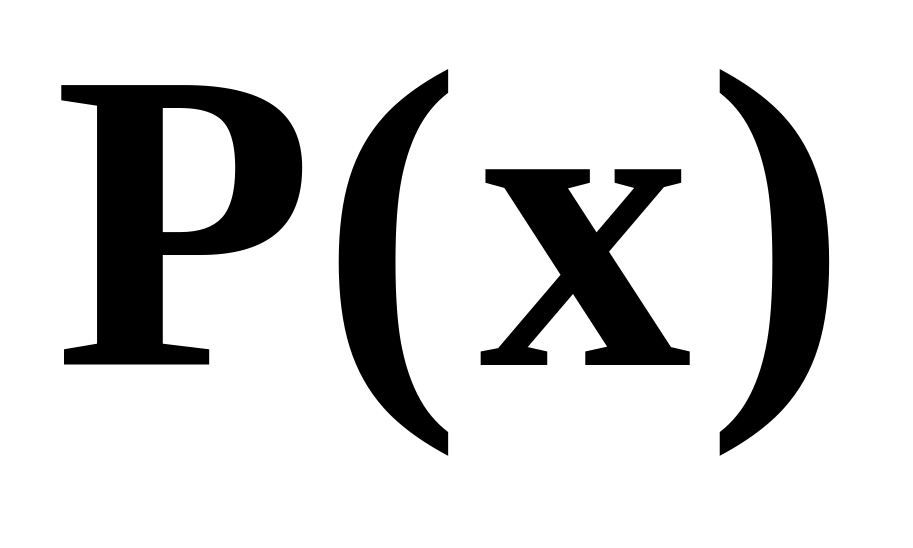 на
на
 .
При домноженні кількість перевірочних
розрядів і, відповідно довжина кодових
слів збільшується на 1. Наприклад, з
(31,26) – коду отримаємо (32,26) – код із
породжуючим поліномом.
.
При домноженні кількість перевірочних
розрядів і, відповідно довжина кодових
слів збільшується на 1. Наприклад, з
(31,26) – коду отримаємо (32,26) – код із
породжуючим поліномом.
![]()
Цей
код виправляє однократні та виявляє
двократні помилки у 32 – розрядних
двоїчних словах. Процедура декодування
аналогічна відповідній процедурі для
кодів Хемінга з
.
Ознакою двократної помилки у цьому
випадку буде неподільність прийнятої
комбінації на
![]() і подільність на
.
і подільність на
.
Коди
БЧХ.
Ці коди отримали свою назву від прізвищ
їх авторів (Р. Боуз, Д. Рой-Чаудхурі та
А. Хоквінгем). Коди БЧХ є узагальненням
кодів Хемінга і дозволяють виправляти
кратні помилки
![]() .
Не заглиблюючись в теорію кодів БЧХ,
зазначимо, що породжуючий поліном для
цих кодів утворюється як найменше
загальне кратне деякої сукупності
непрводимих поліномів (у більшості
випадків – це добуток поліномів). Деякі
з кодів БЧХ наведені у таблиці 2.1.
.
Не заглиблюючись в теорію кодів БЧХ,
зазначимо, що породжуючий поліном для
цих кодів утворюється як найменше
загальне кратне деякої сукупності
непрводимих поліномів (у більшості
випадків – це добуток поліномів). Деякі
з кодів БЧХ наведені у таблиці 2.1.
Таблиця 2.1

