Задания для самостоятельной работы

Исследуйте функцию на возрастание (убывание) и экстремумы:

А. 1) 2) 3) 4)

5) 6)

Б. 1) ; 2) ; 3) ;

4) ; 5)

В. 1) ; 2) ; 3) ;

4) ; 5) ; 6)

4.3. Исследование функции на экстремум с помощью второй производной. Точки перегиба.

Справочный материал

Второй достаточный признак существования экстре­мума. Если в критической точке вторая производная функции от­рицательна, то функция в этой точке имеет максимум. Если вторая производная положительна, — минимум.

Говорят, что функция у = f(х) имеет выпуклость вверх (выпуклость), если график этой функции на (а, b) расположен ниже любой касательной к графику функции на (а, b). Функция выпукла вниз (вогнута) на (а, b), если график этой функции рас­положен выше касательной на (а,b).

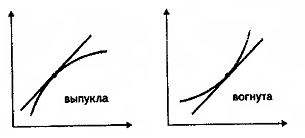
Если функция у = f(x) имеет на интервале (а, b) вторую производную и f"(х)>0 (f"<0) во всех точках (а, b), то функция у = f(х) имеет на (а, b) вогнутость (выпуклость).

Точка перегиба функции — это точка, в которой направле­ние выпуклости меняется на обратное. Например, функция у = х³ имеет точку перегиба

х = 0:

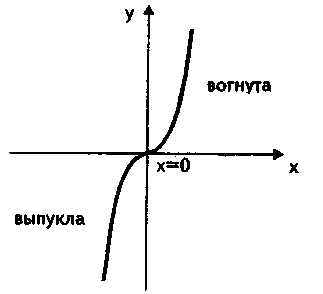
Необходимое условие точки перегиба. Если функция у = f(х) имеет перегиб в точке х, и существует вторая произ­водная в этой точке, тогда

f"(х₀) = 0.

Достаточное условие точки перегиба. Пусть функция у = f(х) имеет вторую производную в некоторой окрестности точки х₀. Тогда, если в пределах этой окрестности f"(х) имеет разные знаки слева и справа от точки х₀, функция f(х) имеет пе­региб в точке х₀.

4.4. Асимптоты кривой.

Справочный материал.

Определение: Асимптотой кривой называется такая прямая, расстояние до которой от переменной точки, движущейся по бесконечной ветви кривой, стремится к нулю.

Функция имеет вертикальные асимптоты в точках, где функция терпит бесконечный разрыв, т.е. если

Значит, если есть точка разрыва 2-го рода,

то прямая - вертикальная асимптота кривой.

Пример 4.5. Найти её вертикальные асимптоты.

РЕШЕНИЕ: терпит бесконечный разрыв при , так как Прямая - вертикальная асимптота. Чтобы уточнить поведение функции вблизи вертикальной асимптоты, находят левый и правый пределы и :

где (-0) и (+0)- символические записи соответственно отрицательной и положительной бесконечно малой величины. График вблизи асимптот представлен на рис. 4.8.

Рис.4.8

Пример 4.6. Найти вертикальные асимптоты функции

РЕШЕНИЕ: имеет две вертикальные асимптоты: и

Для уточнения поведения вблизи вертикальной асимптоты найдём левый и правый пределы и

График вблизи асимптот изображён на рис. 4.9.

Функция не имеет вертикальных асимптот. (Почему?) Функция имеет вертикальную асимптоту Кроме вертикальных асимптот, функция может иметь и наклонные асимптоты, в частном случае - горизонтальные. Эти асимптоты находят по уравнению прямой с угловым коэффициентом при

Рис.4.9

Пусть функция имеет наклонную асимптоту при Найдём и Обозначим через

(1)

По определению асимптоты Разделим равенство (1) на х и перейдём к пределу при где причём наклонная асимптота при существует тогда и только тогда, когда оба эти предела существуют и конечны, в противном случае кривая не имеет наклонной асимптоты.

Аналогично находится уравнение наклонной асимптоты при Если то асимптота будет горизонтальной и её уравнение имеет вид где

Пример 4.7. Найти асимптоты кривой

РЕШЕНИЕ:

точка бесконечного разрыва функции (2-го рода).

Вертикальная асимптота :

;

Наклонная асимптота :

;

Наклонная асимптота: (рис. 4.10).

Рис. 4.10