2. Пределы и непрерывность

2.1. Свойства пределов. Простейшие пределы.

Практическое вычисление пределов основывается на следующих свойствах.

Если существуют конечные пределы , , то:

1. 

2. 

3. т.е.

4. Для

5. Если предел одной или нескольких функций равен бесконечности, то можно воспользоваться следующим соотношениями:

для

6. Если предел функции равен 0, то

Для того, чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.

Примеры.

1. 

2. т.к. при является б.б.в., то при является б.м.в., тогда по определению бесконечно малой величины. Или ;

3. т.к. при является бесконечно малой величиной, тогда -бесконечно большая величина; т.е. функция является бесконечно большой величиной, т.е. по определению бесконечно большой величины.

Или

2.2. Раскрытие неопределенностей различных типов.

Случаи, в которых подстановка предельного значения в функцию не дает значения предела называют неопределенностями; к ним относят неопределенности видов:

Устранить неопределенность удается часто с помощью алгебраических преобразований.

Пример.

Найти

РЕШЕНИЕ

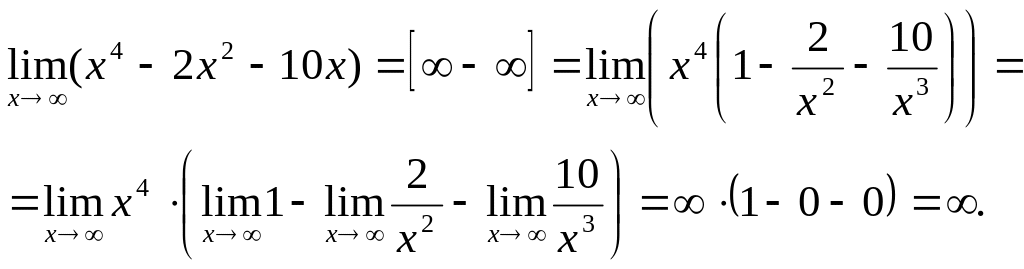
Ответ данной задачи будем использовать далее как заранее известный факт.

2.2.1. Раскрытие неопределенности типа .

В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби x с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое, среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.

Пример.

Задания для самостоятельной работы

1) 3)

2) 4)

2.2.2. Раскрытие неопределенности типа .

В этом случае обычно используются следующие приемы:

1. алгебраические преобразования числителя и знаменателя дроби, приводящие к формулам сокращенного умножения; неопределенность устраняется после сокращения дроби;

2. вынесение в числителе и знаменателе дроби степени х с наименьшим показателем;

3. Деление числителя дроби на ее знаменатель;

4. Эквивалентность бесконечно малых величин;

5. Первый замечательный предел.

Примеры.

a)

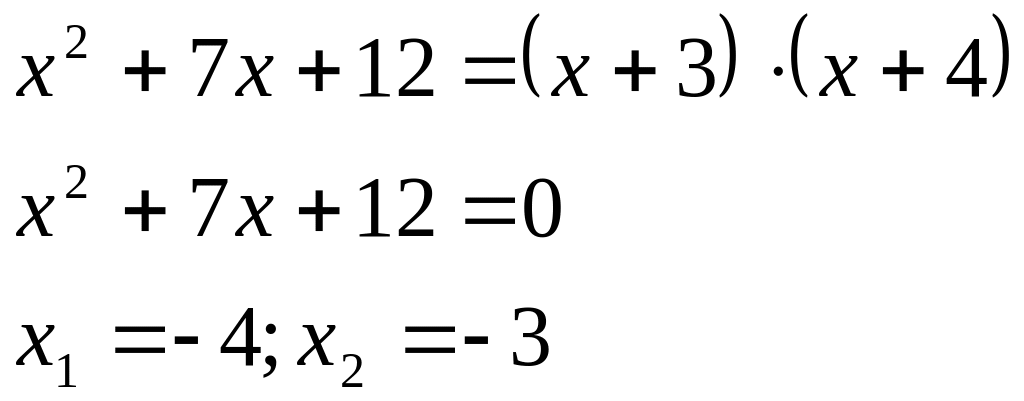
(дополнили числитель до разности квадратов , а знаменатель до разности кубов ).

b)

c)

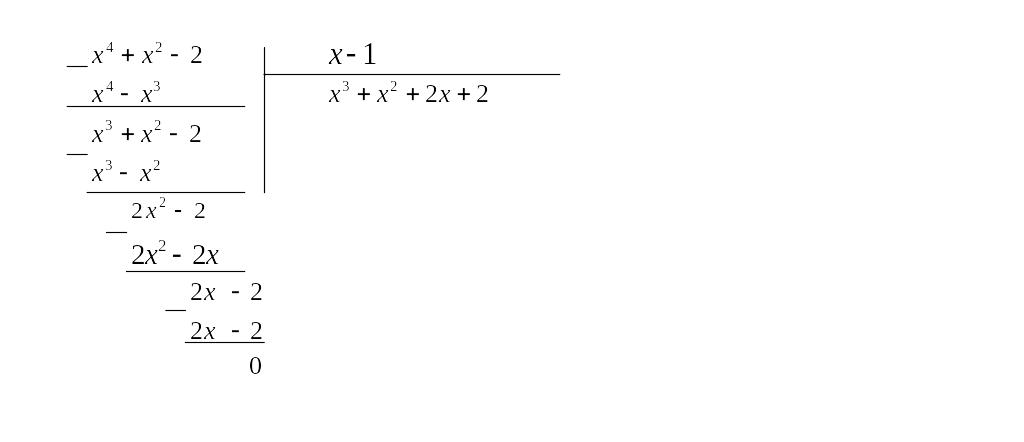
d) Примеры эквивалентных бесконечно малых величин при :

Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые величины заменить им эквивалентными.

Пример.

e) - первый замечательный предел.

Примеры.

1)

2)

2.2.3. Раскрытие неопределенности типа .

В этом случае выражение, стояще под знаком предела представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи «второго замечательного предела».

1) ; 2)

Примеры

1)

2)

3)