Свойства функции

1. Область определения показательной функции — вся числовая

прямая: х R.

2. Множество значений— вся положительная полуось: у > 0.

3. Показательная функция является функцией об­щего вида.

4. График функции проходит через точку с коорди­натами (0; 1).

5. Если а> 1, функция возрастает во всей области определения;

при 0 < а < 1 — убывает. На рис. 1.13 представлены примеры

графиков показательной функции.

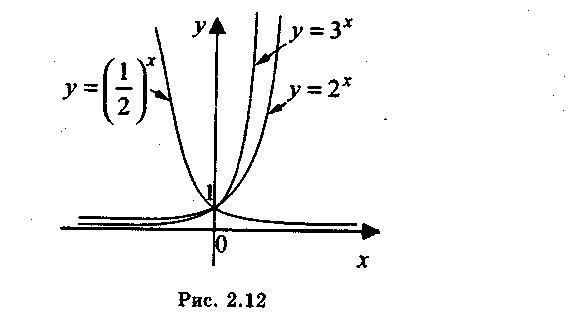Рис. 1.13.

Логарифмическая функция у = log_a x, где а > 0, а 1

Свойства функции

1. Область определения логарифмической функции – положительная

полуось: х >0.

2. Множество значений - вся числовая прямая: y R.

3. Логарифмическая функция является функцией общего вида.

4. График функции проходит через точку с коорди­натами (1; 0).

5. Если а> 1, логарифмическая функция возрастает во всей области

определения; при 0 < а < 1 — убывает.

На рис. 1.14 представлены графики логарифмической функции.

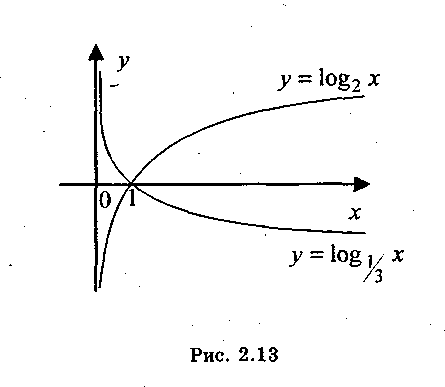Рис. 1.14.

Преобразование графика функции

1. Смещение графика параллельно оси ординат

График функции у = f(x) + а получается из графика функции у = f(x) параллельным смещением его на |а| единиц по оси Оу вверх, если а >0 , или вниз, при а <0 (рис. 1.15).

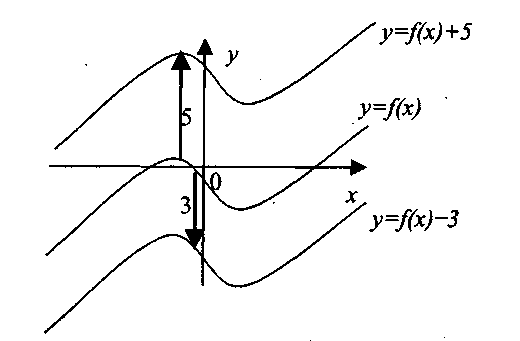
Рис. 1.15

2. Смещение графика параллельно оси абсцисс

График функции у = f(x - а) получается из графика функции у = f(x)

его параллельным смещением вдоль оси Ох на |а| единиц вправо,

если а >0 , или влево, при а <0 (рис. 1.16).

y

x

x

Рис. 1.16.

3. Сжатие и растяжение графика функции

График функции у = kf(x), где k > 0 получается из графика функции у = f(x) путем его сжатия, если 0<k < 1, или растяжения, при k > 1от оси абсцисс в k раз (рис 1.17).

График функции у = f(kx), где k > 0 получается из графика функции

у = f(x) путем его сжатия, если k > 1 к оси ординат в k раз, или растяжения, если 0 < k < 1 от оси ординат в 1/k раз. Например, график функции у = cos 3x получается из графика функции у = cos x сжатием к оси ординат в 3 раза

(рис. 1.18).

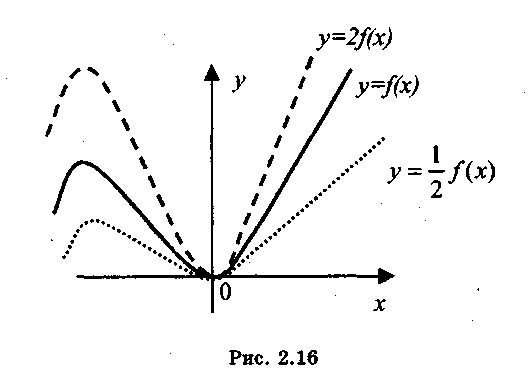
Рис. 1.17.

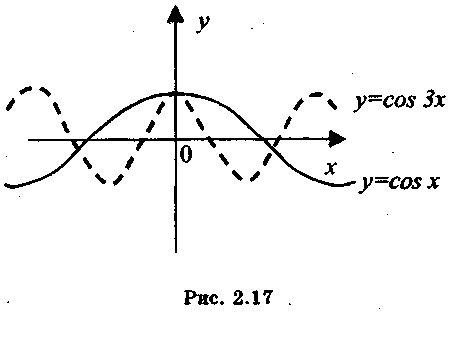
Рис. 1.18

4. Симметричное отображение относительно координатных осей.

График функции у = - f(x) получается из графика функции у = f(x) симметричным отображением относительно оси абсцисс (рис 1.19).

График функции у = f(-x) получается из графика функции у = f(x) симметричным отображением относительно оси ординат (рис 1.20).

Рис. 1.19. Рис. 1.20.

График функции получается из графика функции у = f(x) симметричным отображением относительно оси Ох той части графика, которая ле­жит ниже оси абсцисс (рис 1.21).

График функции получается из графика функции у = f(x) симметричным отображением относительно оси Оу той части графика, которая лежит справа от оси ординат Оу (рис 1.22).

Рис. 1.21.

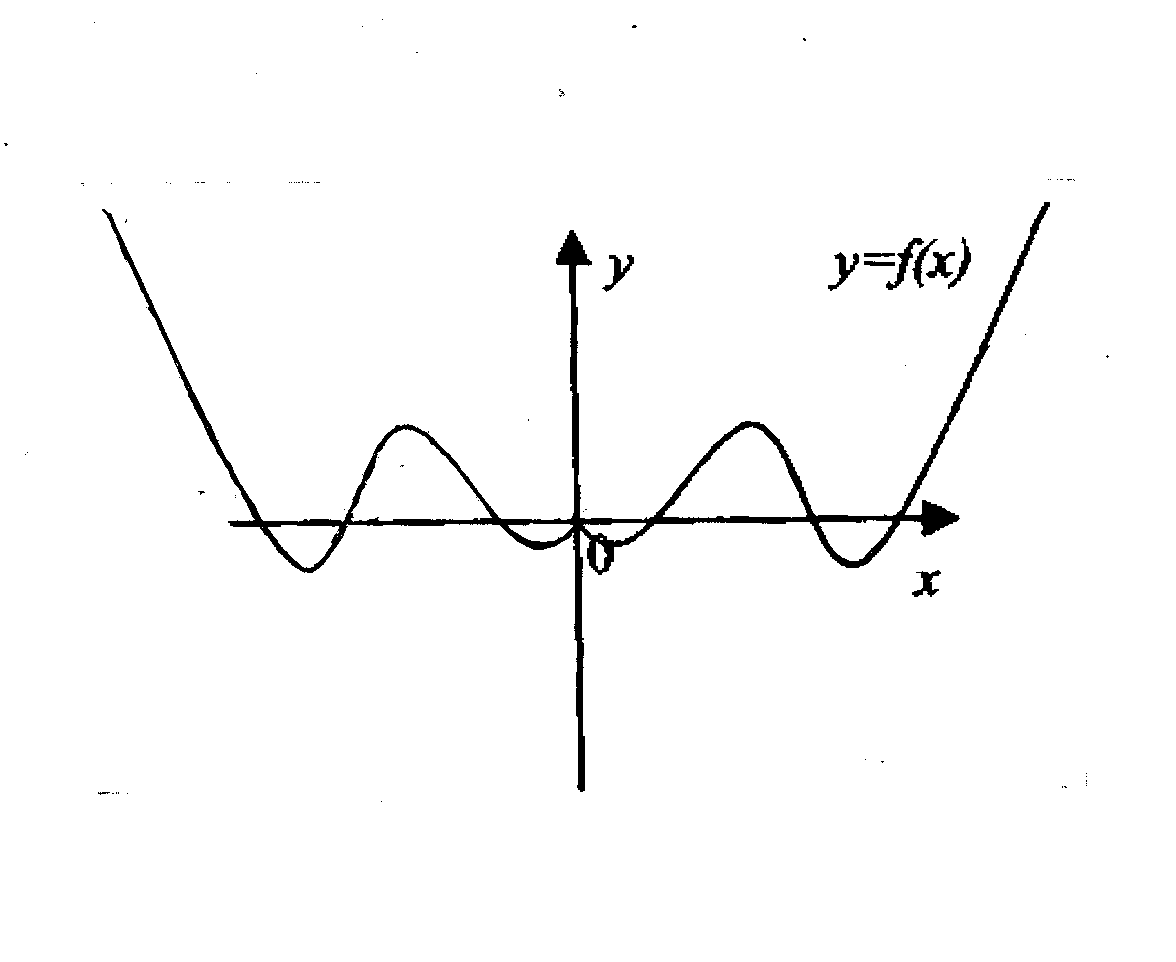Рис. 1.22

Задания для самостоятельной работы

Постройте график функции

1. y=2;	2. х=4;
3. у = 3x;	4. у =2x+1
5. у = -Зх + 2;	6.
7.	8.
9.	10.
11. ;	12.
13.	14.
15. у = 3x2	16.
17. y = -х2 + 7х- 6;	18. у = х2 + 2х + 6;
19. у = -2x2 + 4x - 7;	20. y= 3x2 + 6x-4;

21.	22.
23. y=x4 ;	24. ;
25.	26.
27.	28.
29. у = log3x;	30. y=ln x;
31.	32.
33.	34.
35. y =	36.
37. у= ;	38.
39. у = ;	40.
41. y =	42.
43.	44.
45.	46.
47.	48.