Свойства квадратичной функции
1.
Область определения — вся числовая
ось, то есть
.
2. Если b = 0, функция у = ах2 + с является четной. При b 0 - функция
общего вида, то есть не является ни четной, ни нечетной.
3. Графиком функции является парабола.
4.
Функция имеет единственную критическую
точку
,
при а
>0
х0 является точкой минимума, а <0 — точкой максимума.
5.
Точку с координатами (х0;
у0),
где
называют
вершиной параболы. Квадратичная парабола
симметрична относительно прямой х
=
х0.
При
построении графика достаточно
отметить точки, через которые проходит
одна из ветвей параболы. Вторая ветвь
получается путем симметричного
отображения первой относительно прямой
Рассмотрим частные случаи.
1. Функция у = х2. Ее графиком является парабола, ветви которой направлены вверх и симметричны относительно оси ординат. Вершина этой параболы находится в начале координат. Строим график параболы (рис. 1.9), для точности построения используем точки (1; 1), (2; 4), (3; 9), принадлежащие ее правой ветви. Левую ветвь получим симметричным отображением правой относительно оси ординат.
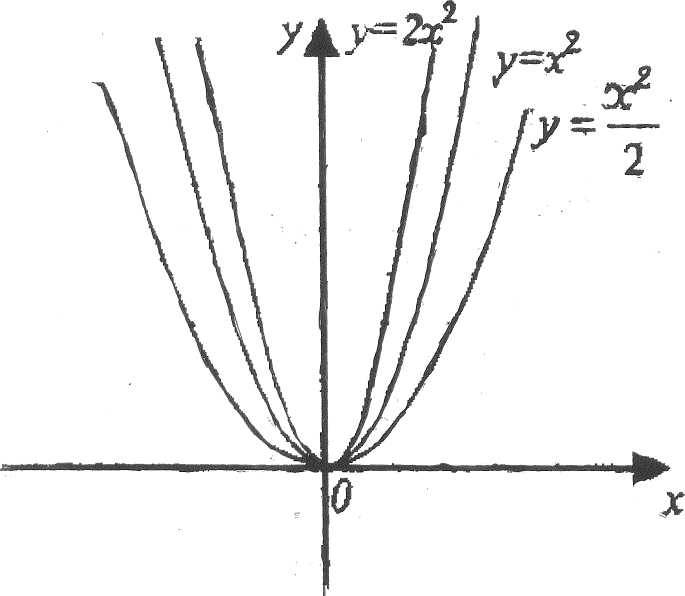
Рис. 1.9.
2. Функция у = ах2. Вершина параболы совпадает с , началом координатной плоскости О (0; 0). Коэффициент а определяет:
1) направление ветвей параболы вверх (а >0) или вниз (а <0);
2) растяжение (при |а| <1) от оси абсцисс или сжатие (при а > 1)
к оси абсцисс в а раз (см. рис. 1.9).
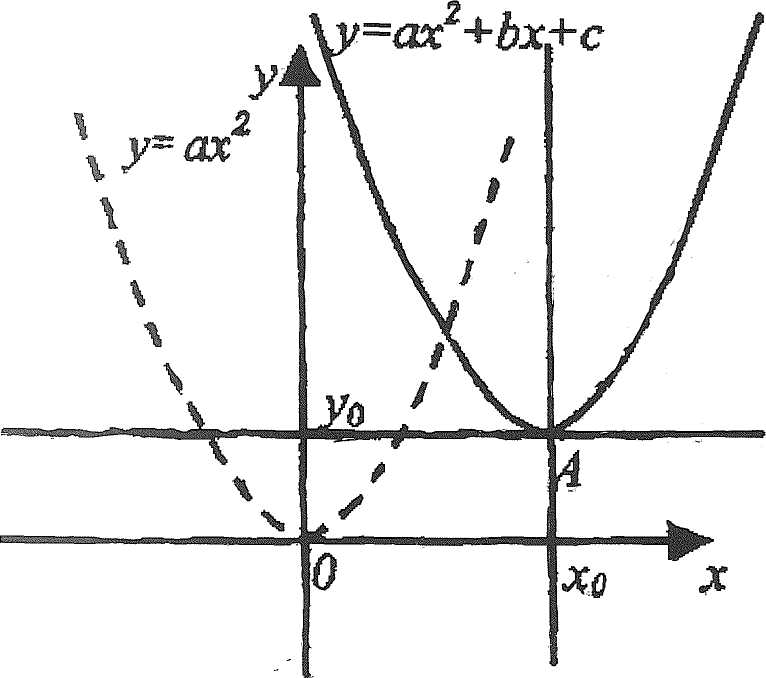
Рис. 1.10.
График функции у = ах2 + bх + с получается из графика функции
у
= ах2
путем
его параллельного переноса сначала
вдоль оси ОХ на
единиц
вправо, если абсцисса вершины параболы
x0>0
, или
влево при x0<0;
затем
вдоль оси Оу на
единиц
вверх, если ордината вершины параболы
у0
>0,
или вниз при y
<0 (рис. 1.10).
Другими словами для построения графика функции у = ах2 + bх + с на координатной плоскости отмечаем вершину параболы А(х0; у0). Параллельным переносом смещаем координатные оси так, чтобы начало координат совпало с точкой А. Относительно новой координатной плоскости строим график функции
у = ах2.
Пример
1.3.
Построить график функции
РЕШЕНИЕ:
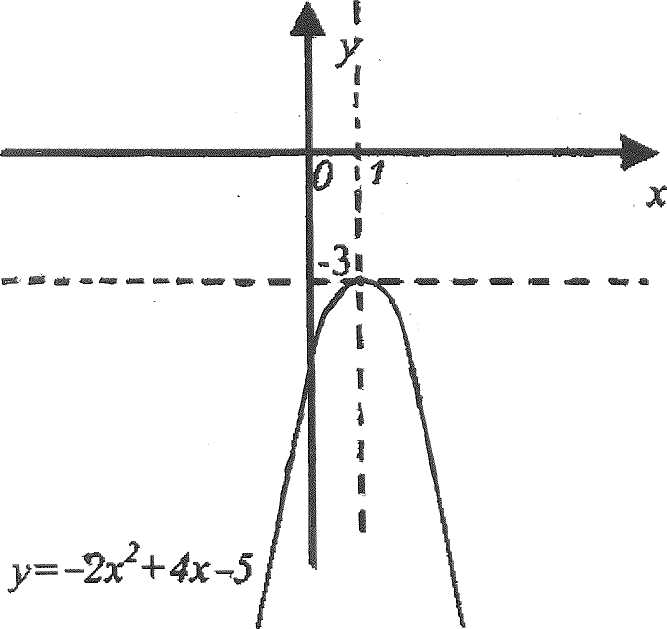Рис.
1.11
Найдем координаты вершины параболы a(x0; y0):
Параллельным переносом смещаем координатные оси так, чтобы начало координат совпало с точкой А(1;-3). Относительно новой координатной плоскости строим график функции у = -2х2 (рис. 1.11).
Степенная
функция у
= ха,
где
а
R
Свойства функции
1. Область определения степенной функции — множество всех
положительных чисел: х >0 ( при х ≤0 выражение ха имеет смысл
не для всех а R).
2. Множество значений степенной функции — множество всех
положительных чисел: у >0.
3. Степенная функция является функцией общего вида.
4. График функции проходит через точку с координатами (1; 1).
При а >0 график функции проходит через начало координат О (0; 0).
5. Если а >0, функция возрастает во всей области определения;
при а <0 — убывает. На рис. 1.12 представлены примеры графиков
степенной функции.
|
|
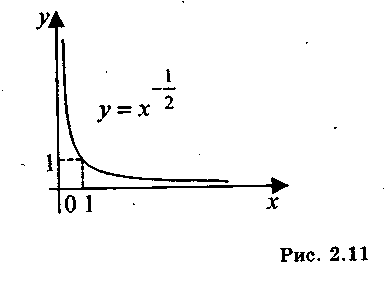
Рис. 1.12.
Показательная функция у = аx, где а > 0, а 1