5. Уточнение корней уравнения методом хорд и касательных:
.
Хорда проведена слева. Касательная
проведена справа.
-
по методу касательных.
Рис. 4.17
5. Предельный анализ в экономике
5.1. Средние и предельные величины
Предположим издержки производства у являются функцией количества выпускаемой продукции х.
Δх – прирост продукции,
Δу – приращение издержек производства;
-
среднее приращение издержек производства
на единицу продукции.
-
выражает предельные издержки производства
и характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
Предельные издержки зависят от уровня производства (количества выпускаемой продукции) х и определяются не постоянными производственными затратами, а лишь переменными (на сырье, топливо и т.п.). Аналогично могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность, предельная производительность и другие предельные величины.
Применение дифференциального исчисления к исследованию экономических объектов и процессов на основе анализа этих предельных величин получило название предельного анализа.
Предельные величины характеризуют не состояние (как суммарная или средняя величина), а процесс, изменение экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесс времени или относительно другого исследуемого фактора).
Рассмотрим в качестве примера соотношения между средним и предельным доходом в условиях монопольного и конкурентного рынков.
Суммарный доход: R=PQ
P - цена единицы продукции, Q – количество продукции.
В условиях монополии, как правило, с увеличением цены спрос падает:
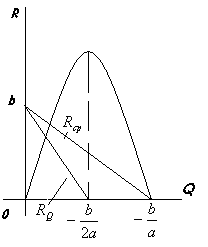
P = aQ+b, где a<0, b>0.
R = (aQ+b)Q = aQ2+bQ
-
средний доход на единицу продукции.
-
предельный доход, т.е. дополнительный
доход от реализации единицы дополнительной
продукции.
В условиях монопольного рынка с ростом количества реализованной продукции предельный доход снижается, что приводит к уменьшению (с меньшей скоростью) среднего дохода.
Монопольный рынок |
Свободный конкурентный рынок
|
|
|
Рис. 5.1.
В условиях совершенной конкуренции число участников рынка велико, каждая фирма не способна контролировать уровень цен, устойчивая продажа товаров возможна по преобладающей рыночной цене. Например,
P = b.
;
;
В условиях свободного конкурентного рынка средний и предельный доходы совпадают.
Примеры использования предельных величин в экономике
Предельные издержки
Экономический
смысл: предельные издержки
равны изменению полных издержек при
изменении выпуска на единицу.
Предельная производительность труда
Экономический смысл: предельная производительность труда изменению объема выпускаемой продукции при изменении численности персонала на единицу.
Y = C+S
C = C(Y) - потребление, S = S(Y) – сбережение.
-
предельная склонность к потреблению;
-
предельная склонность к сбережению.
