
11 Класс. Коллоквиума по геометрии
Часть 1«Основы планиметрии»
Внешний угол треугольника. Определение. Свойство.
Определение. Внешний угол – угол, дополняющий внутренний угол до 180 градусов.
Свойство: 1. Величина внешнего угла треугольника равна сумме величин двух внутренних углов треугольника не смежных с ним.
Теорема о сумме углов треугольника. Следствие из теоремы.
Теорема. Сумма углов треугольника равна 180 градусов.
Следствие.1. У любого треугольника хотя бы 2 угла острых.
Следствие.2. Величина внешнего угла равна сумме величин двух внутренних углов треугольника не смежных с ним.
Следствие.3. Сумма внешних углов равна 360 градусов.
Определение средней линии треугольника. Свойства средней линии треугольника.
Определение 1. Средняя линия треугольника – отрезок соединяющий середины двух его сторон.
Свойство: 1. Средняя линия параллельна одной из его сторон (основанию) и равна половине этой стороны.
Определение медианы, биссектрисы и высоты треугольника.
Определение 2 . Медиана треугольника – отрезок концы которого соединяют вершины треугольника и середину противоположной стороны.
Определение 3. Биссектриса треугольника– это отрезок биссектрисы угла, от вершины до точки пересечения с противоположной стороной.
Определение 4. Высота треугольника- это перпендикуляр, опущенный из любой вершины на противоположную сторону или ее продолжение.
Свойства биссектрисы угла треугольника. Формула для вычисления длины биссектрисы треугольника.
Свойство: 1. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам .
Свойство: 2. Биссектрисы треугольника пересекаются в одной точке (центр вписанной окружности)
Свойство: 3. Биссектриса равноудалена от сторон треугольника.
Формула для вычисления величины биссектрис:
 ,
где а,b
стороны «прилежащие» к биссектрисе
,
где а,b
стороны «прилежащие» к биссектрисе
x, y отрезки на которые биссектриса разбивает третью сторону.
Свойства медианы треугольника. Формула для вычисления длины медианы треугольника.
Свойство: 1. Медианы пересекаются в одной точке. (центр тяжести)
Свойство: 2.Точкой пересечения медианы делятся в отношении 2:1 считая от вершины.
Свойство: 3. Каждая медиана делит треугольник на два равновеликих треугольника.
Свойство: 4. Три медианы делят треугольник на шесть равновеликих треугольника.
Формула для вычисления величины медианы:
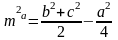 или
или
 ,
где а,b,
с стороны треугольника.
,
где а,b,
с стороны треугольника.
Центр вписанной и центр описанной окружности.
Определение 1. Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник – описанным около этой окружности.
Теорема 1. В любой треугольник можно вписать окружность и при этом только одну. Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Определение 2. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник – вписанным в эту окружность.
Теорема 2. Около любого треугольника можно описать окружность и при этом только одну. Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
Отношение периметров, площадей, высот подобных фигур.
Свойство
1.Отношение
периметров и высот подобных фигур равно
коэффициенту подобия
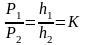
Свойство
2. Отношение площадей
подобных фигур равно квадрату коэффициента
подобия
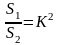 .
.
Теорема косинусов. Следствия: связь между диагоналями и сторонами параллелограмма; определение вида треугольника; формула для вычисления длины медианы треугольника; вычисление косинуса угла треугольника.
Теорема 1. Теорема косинусов – квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
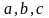 стороны
треугольника и угол
стороны
треугольника и угол  ,
противолежащий стороне
,
противолежащий стороне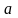 .
.
Следствие 1. Следствие из теоремы косинусов (о связи диагоналей и сторон параллелограмма). Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
d12 + d22 = 2 a2 + 2 b2
Следствие 2. Следствие из теоремы косинусов об определении вида треугольника.
Пусть с- наибольшая сторона треугольника.
Если с2=а2+b2, то угол против с=90 градусов и треугольник прямоугольный.
Если с2<а2+b2, то угол против с<90 градусов и треугольник остроугольный.
Если с2>а2+b2, то угол против с>90 градусов и треугольник тупоугольный.
Формула 1. Формулы для вычисления длины медианы треугольника.
или
Формула 2.
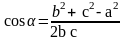 ,
угол
лежит
напротив стороны а.
,
угол
лежит
напротив стороны а.
Теорема синусов. Следствие теоремы синусов( о радиусе описанной окружности).
Теорема 1. Теорема синусов – стороны треугольника пропорциональны синусам противолежащих углов.
![]()
где ![]() ,
, ![]() ,
, ![]() —
стороны треугольника,
—
стороны треугольника, ![]() —
соответственно противолежащие им углы.
—
соответственно противолежащие им углы.
Следствие 1. Следствие из теоремы синусов (о радиусе описанной окружности). Диаметр описанной окружности около треугольника равен отношению стороны треугольника к синусу противоположного угла.
![]()
где
,
,
—
стороны треугольника,
—
соответственно противолежащие им углы,
а ![]() —
радиус окружности,
описанной вокруг треугольника.
—
радиус окружности,
описанной вокруг треугольника.
Свойства прямоугольного треугольника
Теорема Пифагора. В любом прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
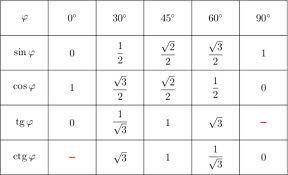
Синус угла х – это отношение противолежащего катета к гипотенузе.
Косинус угла х – это отношение прилежащего катета к гипотенузе.
Тангенс угла х – это отношение противолежащего катета к прилежащему.
Котангенс угла х – это отношение прилежащего катета к противолежащему.
Свойство высоты прямоугольного треугольника, опущенного на гипотенузу.
Свойство: 1. В любом прямоугольном треугольнике, высота, опущенная из прямого угла( на гипотенузу), делит прямоугольный треугольник, на три подобных треугольника.
Свойство: 2. Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу(или среднему геометрическому тех отрезков на которые высота разбивает гипотенузу).
Свойство: 3. Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Свойство: 4. Катет против угла в 30 градусов равен половине гипотенузы.
Формула
1.
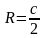 ,
где
,
где
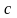 гипотенуза;
гипотенуза;
Формула
2.
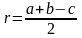 ,
где
гипотенуза;
,
,
где
гипотенуза;
,
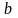 катеты.
катеты.
Свойство: 5. В прямоугольном треугольнике медиана проведенная к гипотенузе, равна ее половине и равна радиусу описанной окружности.
Свойство: 6. Зависимость между сторонами и углами прямоугольного треугольника:
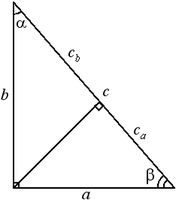
![]() ;
;
![]() ;
;
![]() .
.
Свойство диаметра перпендикулярного хорде.
Свойство: 1. Диаметр перпендикулярный хорде делит эту хорду пополам.
Свойство дуг, заключенных между параллельными хордами.
Свойство: 1. Дуги, заключенные между параллельными хордами, равны.
Свойства касательной.
Определение. Касательная – прямая, имеющая только одну точку пересечения с окружностью.
Свойство: 1. Касательная к окружности перпендикулярна к радиусу проведенного в точку касания.
Свойство: 2. Две касательные проведенные из одной точки к окружности – равны.
Определение вписанного угла, центрального угла. Измерение их величин. Свойство вписанного угла, его связь с центральным углом, опирающимся на туже хорду.
Определение 1. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность – вписанный угол.
Определение 2. Центральный угол в окружности – плоский угол с вершиной в ее центре.
Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Свойство: 1. Все вписанные углы, опираются на одну и ту же дугу, равны между собой.
Свойство: 2. Вписанный угол, опирающийся на диаметр прямой.
Угол с вершиной внутри круга; угол с вершиной вне круга; угол межу касательной и хордой. Измерение их величин.
Свойство: 1. Угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, из которых одна заключается между его сторонами, а другая между продолжениями сторон.
Свойство: 2. Угол, вершина которого лежит вне круга, измеряется полуразностью двух дуг, заключенных между его сторонами.
Свойство: 3. Угол, составленный касательной и хордой, измеряется половиной дуги заключенной внутри него.
Свойство хорд, пересекающихся в круге.
Свойство:
1. Если хорды,
АВ и СD
окружности пересекаются в точке S,
то AS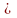 ВS=DS
CS.
ВS=DS
CS.
Свойство секущей и касательной, проведенной из одной точки.
Свойство: 1. Произведение отрезков секущей окружности равно квадрату отрезка касательной, проведенной из той же точки.
Свойство секущих, проведенных из одной точки.
Если из одной точки P к окружности проведены две секущие, пересекающие окружность в точках A,B,C,D соответственно, то AP ВP=CP DP.
Свойства вписанного и описанного четырехугольника.
Свойство: 1. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равна 180 градусов.
Свойство: 2. Четырехугольник можно описать около окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
Правильный многогранник. Формулы для вычисления радиусов вписанной и описанной окружности.
Определение
1. Правильный
многоугольник
— это выпуклый многоугольник,
у которого все стороны между собой равны
и все углы между собой равны.
Площадь правильного многоугольника

Формула
1. Для радиуса окружности, описанной
около правильного n-угольника.
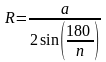
Формула 2. Для радиуса окружности, вписанной в правильный n-угольник.

Правильный четырехугольник.
Диагональ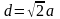
Площадь квадрата (через
сторону; через диагональ).
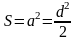
Радиус вписанной
окружности
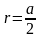
Радиус описанной
окружности
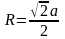 .
.
Правильный треугольник
Высота
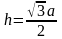
![]() ,
,
![]()
![]()
Правильный шестиугольник
Большая диагональ
равна
 ,
меньшая
,
меньшая
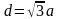 ,
,
 ,
,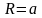 .
.
Формула для нахождения
величины угла правильного многоугольника.
Величина угла правильного многоугольника
равна
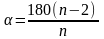 .
.
Площадь правильного шестиугольника.

Определение равновеликих фигур.
Определение. Фигуры называется равновеликими – если их площади равны.
Формулы для вычисления площади:
Площадь прямоугольника
(через сторону; через диагональ).
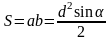
Площадь параллелограмма
(через высоту; через угол; через диагонали).
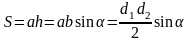
Площадь ромба (через
угол; через диагонали; через высоту).
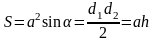
Площадь трапеции.
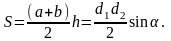
Площадь выпуклого
четырехугольника.
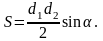
Площадь правильного треугольника.
Площадь правильного шестиугольника.
Площадь треугольника
(через две стороны и угол между ними)
равна половине произведения сторон
треугольника и на синус угла между ними.
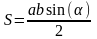
Площадь треугольника
(через высоту) равна половине произведения
основания на высоту. .
.
Площадь треугольника
(формула Герона).
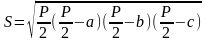
Площадь квадрата (через сторону; через диагональ).
Площадь
круга.
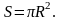
Площадь кругового
сектора.
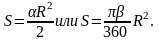 (
-угол
в радианах,
(
-угол
в радианах,
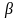 угол в градусах )
угол в градусах )
Площадь кругового
сегмента.
 -угол
в радианах,
угол в градусах )
-угол
в радианах,
угол в градусах )
Площадь описанного
многоугольника
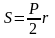 .
.
Формулы для вычисления площади треугольника через радиусы.
Площадь
треугольника (через радиус описанной
окружности; через радиус вписанной
окружности).
 .
.
Вектор. Координаты вектора. Длина вектора.
Определение.
Вектор- это направленный отрезок имеющий
начало и конец. Обозначается например
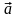 или
или
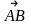 .
.
Пусть
А -
начало вектора и B
-
начало вектора и B
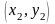 -
конец вектора
-
конец вектора
Тогда
координатами вектора
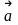 называются
называются
 ,
где
,
где
 ,
,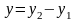 ;
;
Длина
вектора
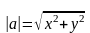 .
.
Равные вектора. Коллинеарные вектора. Их свойства.
Два вектора называются равными, если они коллиниарные и имеют одинаковую длину и направление.(равные вектора имеют равные координаты).
Вектора называются коллинеарными, если существует прямая, которой они параллельны.
Коллинеарные вектора – это вектора, у которых координаты пропорциональны.
Пусть
вектор
-
вектор
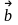 ,
тогда
,
тогда
 .
.
Координаты середины отрезка.
Если
необходимо найти т. С (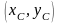 ,середину
отрезка АВ,(т.А
,середину
отрезка АВ,(т.А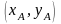 , т.B
, т.B ),
тогда координата точки С
,
равна
),
тогда координата точки С
,
равна
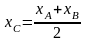 ,
,
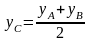 .
.
