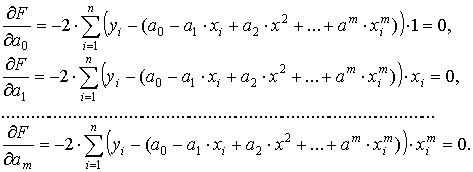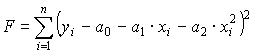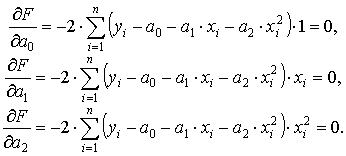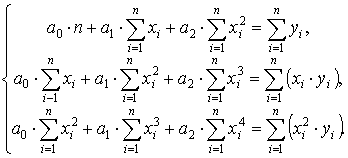Лабораторная работа № 5. Приближение функций

Цель работы: научиться аппроксимировать функции, задаваемые таблично методом наименьших квадратов с помощью ЭВМ.

Программа работы

1. Изучить методы приближения функций методом наименьших квадратов

2. На конкретном примере усвоить порядок приближения функций

методом наименьших квадратов с помощью ЭВМ указанными методами.

3. Составить программу(ы) на любом языке программирования, реализующую(ие) приближения функций используя алгоритмы метода наименьших квадратов. Печать результатов должен осуществляться на каждом шаге итераций

4. Для заданного варианта решить с помощью программы приближения функций многочленом второй степени

5. Для заданного варианта подобрать эмпирическую формулу.

6. Составить отчет о работе.

Содержание отчета.

Отчет по лабораторной работе должен содержать следующие материалы: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы; листинг(и) программ(ы); таблицы результатов (в случае, если число итераций в таблице достаточно большое, в отчет занести две первых и две последних итерации); графический материал ; выводы о работе.

Варианты заданий даны в приложениях А и В.

Пояснения к работе

Пусть функция f(x) задана на отрезке [a,b] таблицей значений f(x_i) в узлах x_i, . Задача приближения (аппроксимации) заключается в следующем: данную функцию f(x) приближенно заменить (аппроксимировать) многочленом заданной степени k так, чтобы отклонение f(x) от P_k(x) было минимальным на заданном множестве точек x_i . Эта функциональная (аналитическая) зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. Критерием точности или достаточно "хорошего" приближения могут служить несколько условий. В зависимости от того, какой критерий близости выбран для решения этой задачи, применяют соответствующий метод аппроксимации.

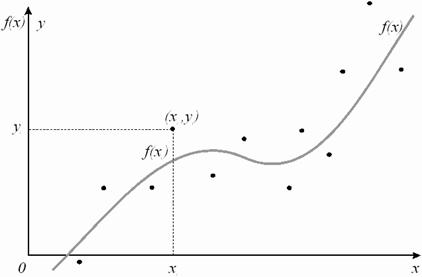
Графическая интерпретация аппроксимации приведена на рисунке 1. 

Метод наименьших квадратов

Рассмотрим наиболее распространенный частный случай приближения функции многочленом : P(x)=a₀+a₁^.x+a₂^.x²+...+a_m^.x^m . (1)

Идея метода наименьших квадратов заключается в том, коэффициенты многочлена определяются так, чтобы сумма квадратов отклонений найденного многочлена от заданных значений функции в точках x_i была минимальна , т.е.

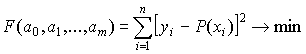
где F(a₀, a₁, …, a_m) - функция коэффициентов.

В точке минимума функции F(a₀, a₁, …, a_m) ее производные обращаются в нуль.

, , …, .

(2)

Используя систему (2), получаем математическое условие минимума для

F(a₀, a₁, …, a_m) :

Отсюда получаем так называемую нормальную систему для определения коэффициентов a_j (j=0, 1, …, m). В результате решения системы линейных уравнений получим коэффициенты а₀,а₁,...,а_m многочлена (1).

Запишем алгоритм метода наименьших квадратов. 1.     Ввести таблицу чисел  . 2.     Вычислить  .

3. Составить систему линейных алгебраических уравнений. 3.     Решить любым известным методом полученную систему и получить коэффициенты искомого многочлена  .

Рассмотрим случай многочлена 2-ой степени

.

(3)

Коэффициенты аj определяются по методу наименьших квадратов. Запишем сумму квадратов отклонений.

(4)

Приравняем к нулю частные производные:

(5)

Выполнив преобразования, получим систему линейных уравнений с тремя неизвестными (а0, а1,а2).

(6)

Введем обозначения:

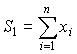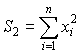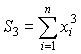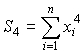; ; ; ; (7)

; ; .

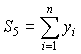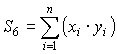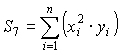С учетом принятых обозначений система (5.34) будет иметь следующий вид:

(8)

Решив систему (5), определим неизвестные коэффициенты a0, a1, a2 многочлена

.

Подбор эмпирических формул

Пусть в результате измерений получена таблица зависимости одной величины от другой

Таблица

Задача состоит в аппроксимации неизвестной функциональной зависимости между x и y эмпирической формулой :

,

(9)

где m - число параметров; a₁…a_m - неизвестные коэффициенты, которая в точках

принимает значения как можно более близкие к табличным значениям

.Функция позволяет найти значения для не табличных значений.

Практически вид приближающей функции можно определить визуально: по таблице строится точечный график функции, а затем проводится кривая, по

возможности наилучшим образом отражающая характер расположения точек

(рис.2).

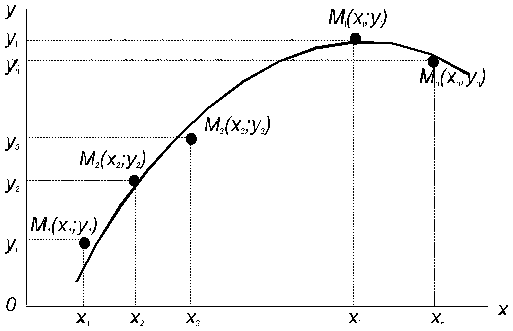
Рис.2

По полученной кривой устанавливается вид приближающей функции (обычно из числа простых по виду аналитических функций: линейная, степенная,

экспоненциальная или показательная, логарифмическая, гипербола, дробно-

рациональная и т.д.).

Затем необходимо подобрать такие значения параметров в формуле, чтобы разница между опытными значениями величины и значениями, найденными по эмпирической формуле , не превышала ошибок эксперимента.

Эмпирическая формула подобрана наилучшим образом, если выполняется условие

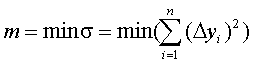
где , - экспериментальное, _- расчетное значения для каждого значения

.

Если эта разница получается слишком большой, берут другой подходящий график и повторяют попытку. Для отыскания неизвестных коэффициентов применим метод наименьших квадратов, который является универсальным методом решения задач аппроксимации.

Рассмотрим наиболее употребляемые формулы и соответствующие им графики
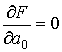
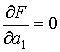
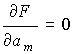