Лекция № 2. Квантово-механическая модель атома. Квантовые числа, их физический смысл.

Цель: изучить квантово-механическую модель атома, квантовые числа и их физический смысл.

План

1. Квантово-механическая модель атома.

2. Квантовые числа, их физический смысл.

3. Принцип Паули, правило Гунда.

1. В 1924 г. французский физик Луи де Бройль высказал идею о том, что материя обладает как волновыми, так и корпускулярными свойствами. Согласно уравнению де Бройля (одному из основных уравнений квантовой механики),

т. е. частице с массой m, движущейся со скоростью v соответствует волна длиной λ; h — постоянная Планка.

Длину волны такой частицы называют длиной волны де Бройля. Для любой частицы с массой т и известной скоростью v длину волны де Бройля можно рассчитать. Идея де Бройля была экспериментально подтверждена в 1927 г., когда были обнаружены у электронов как волновые, так и корпускулярные свойства. В 1927 г. немецким ученым В. Гейзенбергом был предложен принцип неопределенности, согласно которому для микрочастиц невозможно одновременно точно определить и координату частицы X, и составляющую р_х импульса вдоль оси х. Математически принцип неопределенности записывают следующими уравнениями:

ΔxΔp_x ≥ h;

ΔxΔp_y ≥ h;

ΔxΔp_z ≥ h.

Отсюда следует, что при точном определении координаты х микрочастицы исчезает информация о ее импульсе Δp_x, так как при х=0 величина Δp_x→∞. Если удастся снизить погрешность Δp,то будет велика погрешность Δх. Источник этих погрешностей заключен не в приборах, а в самой природе вещей.

Поскольку постоянная Планка очень мала, то ограничения, накладываемые принципом неопределенности, существенны только в масштабах атомных размеров. Согласно принципу неопределенности, невозможно утверждать, что электрон, имеющий определенную скорость, находится в данной точке пространства, здесь можно использовать лишь вероятностное описание.

Для описания свойств электрона используют волновую функцию, которую обозначают буквой Ψ (пси). Квадрат ее модуля |Ψ|², вычисленный для определенного момента времени и определенной точки пространства, пропорционален вероятности обнаружить частицу в этой точке в указанное время. Величину |Ψ|² называют плотностью вероятности. Наглядное представление о распределении электронной плотности атома дает функция радиального распределения. Такая функция служит мерой вероятности нахождения электрона в сферическом слое между расстояниями r и (r+dr) от ядра. Объем, лежащий между двумя сферами, имеющими радиусы r и (r+dr), равен 4Πr²dr, а вероятность нахождения электрона в этом элементарном объеме может быть представлена графически в виде зависимостей функции радиального распределения. На рис. 1 представлена функция вероятности для основного энергетического состояния электрона в атоме водорода. Плотность вероятности |Ψ|² достигает максимального значения на некотором конечном расстоянии от ядра. При этом наиболее вероятное значение r для электрона атома водорода равно радиусу орбиты a₀ соответствующей основному состоянию электрона в модели Бора. Различная плотность вероятности дает представление об электроне, как бы размазанном вокруг ядра в виде так называемого электронного облака (рис. 2).

 

Рис. 1. Радиальное распределение  вероятности пребывания электрона для основного энергетического состояния атома водорода

Рис. 2. Электронное s-облако (l - 0)

 

Чем больше величина |Ψ|², тем больше вероятность нахождения электрона в данной области атомного пространства.

В квантовой механике вместо термина «орбита» используют термин «орбиталь», которым называют волновую функцию электрона. Соответственно орбиталь характеризует и энергию и форму пространственного распределения электронного облака. Расчеты в квантовой механике проводят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном-пространстве.

В простейшем случае уравнение Шредингера может быть записано в виде

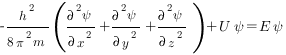
где h — постоянная Планка; m — масса частицы; U — потенциальная энергия; Е — полная энергия; х, у, z — координаты; Ψ — волновая функция.

Решая уравнение Шредингера, находят волновую функцию Ψ=f(x, y, z). Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию можно оценить величину |Ψ|²dV — вероятность нахождения электрона в объеме пространства dV, окружающего атомное ядро. Решение уравнения Шредингера представляет сложную математическую задачу.

2. Состояние электрона в атоме описывают с помощью 4 чисел, которые называют квантовыми: 

Квантовое число	Символ	Описание	Значения
Главное	N	Энергетический уровень орбитали	Положительные целые числа:1, 2, 3...
Орбитальное	L	Форма орбитали	Целые числа от 0 до n-1
Квантовое	M	Ориентация	Целые числа от -l до +l
Спиновое	ms	Спин электрона	+½ и -½

Главное квантовое число n

Описывает:

1. среднее расстояние от орбитали до ядра;

2. энергетическое состояние электрона в атоме.

Чем больше значение n, тем выше энергия электрона и больше размер электронного облака. Если в атоме несколько электронов с одинаковым n, то они образуют электронные облака одинакового размера - электронные оболочки.

Орбитальное квантовое число l (азимутальное)

Описывает форму орбитали, которая зависит от n.  Орбитальное число l может принимать целочисленные значения в диапазоне от 0 до n-1. Например, при n=2: l=0 l=1 

Значение l определяет форму орбитали, а n - ее размер

Орбитали, имеющие одинаковое n, но разные l называют энергетическими подуровнями и обозначают буквами латинского алфавита: 

l	Энергетический подуровень
0 1 2 3 4	s p d f g

Состояние электрона в атоме для различных главных и орбитальных квантовых чисел принято записывать следующим образом: 2s; 3p; 3d…

Магнитное квантовое число m

Описывает ориентацию орбиталей в пространстве.  Может принимать целочисленные значения в диапазоне от -l до +l (включая 0). Например:  Для l=0 возможно только одно значение: m=0. Это значит, что s-орбиталь имеет только одну пространственную ориентацию.  Для l=1: m=-1;0;+1 - p-орбиталь имеет три пространственные ориентации.  Для l=2: m=-2;-1;0;+1;+2 - d-орбиталь имеет пять пространственных ориентаций.

Спиновое квантовое число m_s

Описывает направление вращения электрона в магнитном поле - по часовой стрелке или против. На каждой орбитали может находиться только два электрона: один со спином +½ другой -½.  Квантовые числа для первых трех энергетических уровней: 

n	L	Орбиталь	m	ms
1	0	1s	0	+½ -½
2	0	2s	0	+½ -½
2	1	2p	-1 0 +1	+½ -½ +½ -½ +½ -½
3	0	3s	0	+½ -½
3	1	3p	-1 0 +1	+½ -½ +½ -½ +½ -½
3	2	3d	-2 -1 0 +1 +2	+½ -½ +½ -½ +½ -½ +½ -½ +½ -½

На первом уровне (n=1) есть только s-орбиталь, на которой может находиться только 2 электрона со спинами +1/2 и -1/2. Это справедливо для s-орбитали любого уровня: 1s; 2s; 3s…  На втором энергетическом уровне (n=2) есть уже две орбитали s; p. На третьем (n=3) - три орбитали: s, p, d. и т.д. С каждым новым энергетическим уровнем добавляется новая орбиталь.  Для 2p-орбитали существует три пространственных ориентации (формы облака), на каждой из которых может находиться по два электрона. Т.е. на втором энергетическом может находиться не более 6 p-электронов.  Для 3d - максимум 10 d-электронов и пять форм облаков.  Главные энергетические уровни отличаются энергией. Чем выше уровень - тем выше энергия. С другой стороны, различные орбитали одного и того же уровня также обладают разной энергией:  Энергия электронов на орбитали 2p выше, чем на 2s.  Энергия электронов на орбитали 3p выше, чем на 3s.  Энергия электронов на орбитали 3d выше, чем на 3s.  Энергия электронов на орбитали 3d выше, чем на 3p.  Что же касается электронов "внутри орбиталей", то их энергии одинаковы (так у всех десяти электронов 3d-орбитали энергии одинаковы).

Контрольные вопросы

1. Какой подуровень заполняется в атоме электронами после заполнения подуровня 4р?

2. Составить электронную формулу атома Кремния и графическую схему заполнения электронами валентных орбиталей этого атома в нормальном и р возбужденном состояниях.

3. На каком основании хлор и марганец помещают в одной группе периодической системы элементов? Почему их поме­щают в разных подгруппах?

4. Сколько значений магнитного квантового числа возможно для электронов энергетического подуровня, орбитальное квантовое число которого Z=2? Z = 3?,

5. Какое, максимальное число электронов может: додержать атом в электронном слое с главным квантовым числом n=4?

6. Определить по правилу Клечковского последо­вательность заполнение электронных орбиталей, характеризующихся суммой п + 1: а) 5; б) 6; в) 7.

7. Указать порядковый номер элемента, у которого: а) заканчивается заполнение электронами ор­биталей 4dб) начинается заполнение подуровня 4р.

8. Какой подуровень заполняется в атомах после подуровня 5s?

9. У какого элемента начинает заполняться под­уровень 4d? У какого элемента завершается заполнение этого подуровня?

10. Какой подуровень заполняется в атомах после заполнения подуровня 5р? После заполнения подуровня 5d?

11. Записать электронные формулы атомов элементов с зарядом ядра-: а) 8; б) 13; в) 18; г) 23; д) 53; е) 63; ж) 83. Составить графические схемы за­полнения электронами валентных орбиталейэтих атомов.