Определение отношения удельных теплоемкостей методом клемáна и дезóрма

Цель лабораторной работы: определение показателя адиабаты воздуха.

Оборудование: баллон с кранами, манометр, груша.

Краткая теория

Теплоемкостью тела называется физическая величина, числено равная количеству теплоты, которую нужно сообщить телу, чтобы повысить его температуру на 1 градус. Теплоемкость, отнесенная к единице массы, называется удельной теплоемкостью c, а к одному молю – молярной теплоемкостью С. Молярная и удельная теплоемкости связаны через молярную массу М: С = Мс. Это соотношение справедливо как для теплоемкости при постоянном давлении, так и для теплоемкости при постоянном объеме.

Важное значение в термодинамике имеет отношение теплоемкости при постоянном давлении с_р к теплоемкости при постоянном объеме с_v. Это отношение называется показателем адиабаты , и его можно определить через число степеней свободы i молекулы газа:  = с_р /c_v = (i + 2) / i. Значение величины  играет большую роль при изучении адиабатических процессов. Например, от этой величины зависит скорость распространения звука в газах и течение газов по трубам со сверхзвуковыми скоростями.

Всякое достаточно быстрое изменение объема газа можно с достаточной степенью точности рассматривать как адиабатическое, т.к. теплообменом с окружающей средой можно пренебречь. При быстром расширении газ охлаждается, а при быстром сжатии – нагревается.

Одним из самых простых методов определения  является метод Клемáна и Дезóрма. Рассмотрим его сущность.

Пусть в закрытом стеклянном баллоне объемом V находится исследуемый газ при комнатной температуре Т₁ и давлении р₁, несколько превышающем атмосферное давление р₀.

Если открыть кран, соединяющий баллон с атмосферой, то давление в сосуде упадет до атмосферного, а температура сначала несколько понизится из-за быстрого расширения газа в атмосферу, а затем поднимется до комнатной (вследствие теплообмена через стенки сосуда). Так как отверстие крана достаточно велико, а теплопроводность стекла низка, то время выравнивания давления t_P во много раз меньше времени выравнивания температуры t_Т. Пусть кран был открыт в течение малого промежутка времени t такого, что t_T   t  t_P. В этом случае можно теплообменом пренебречь и считать процесс выхода газа в атмосферу адиабатическим. Уравнение адиабаты в переменных р и Т запишем в виде:

(1)

Заметим, что в конце адиабатического расширения давление р₂ равно атмосферному р₀, а температура Т₂ оказывается несколько ниже комнатной температуры Т₁. Затем, если кран на баллоне закрыт, то вследствие теплообмена с окружающей средой происходит медленное изохорное нагревание газа до тех пор, пока установившаяся температура газа Т₃ не сравняется с комнатной Т₁. Для изохорного процесса можно записать:

(2)

Исключая с помощью уравнения (2) отношение температур из (1), найдем:

(3)

Разрешим это уравнение относительно :

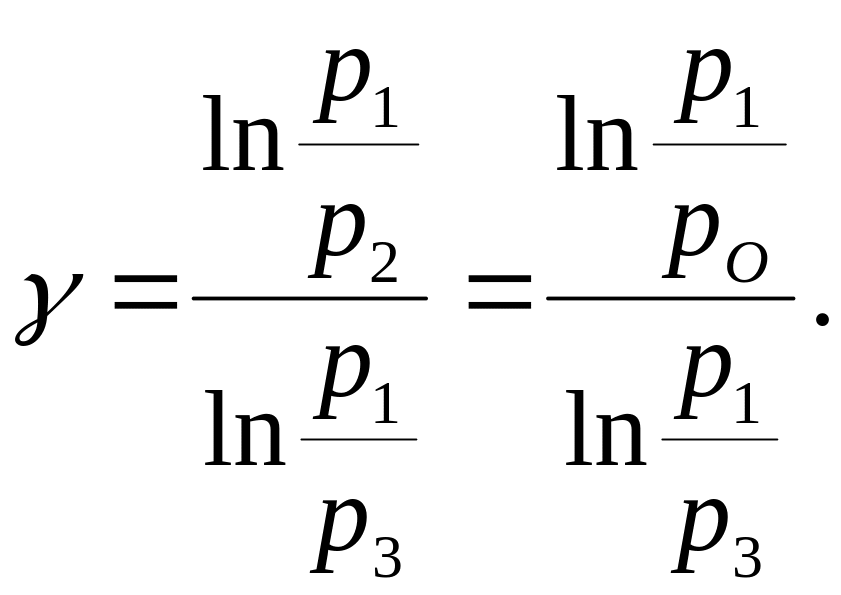(4)

В нашем случае давления р₁ и р₃ мало отличаются от атмосферного р₀ и формулу (4) можно существенно упростить. Введем обозначения:

р₁ = р₀ + h₁, p₃ = p₀ + h₂.

Разлагая логарифмы в ряд и пренебрегая членами второго порядка малости, получим:

⁽⁵⁾

Как видно из уравнения (5), для вычисления  необходимо измерить избыточное давление в баллоне до адиабатического расширения газа h₁ и его избыточное давление после изохорного нагревания h₂. Следует подчеркнуть, что обе величины должны измеряться в состоянии термодинамического равновесия, т.е. после прекращения теплообмена.