
- •4.1. Необхідна умова існування екстремуму функції двох змінних.
- •4.2. Достатня умова існування екстремуму функції двох змінних
- •4.3. Приклади та задачі для самостійної роботи.
- •4.4 Умовні екстремуми функції двох змінних
- •4.5. Приклади для самостійної роботи.
- •4.6. Знаходження найбільшого та найменшого значень функції двох змінних
- •4.7 Приклади та задачі для самостійної роботи.
- •Бібліографічний список
- •Глава 1. Матриці та дії над ними……................................................................. 4
- •Глава 2. Системи лінійних алгебраїчних рівнянь ................................................. 33
- •Глава 3. Екстремуми функції однієї змінної ............................................................ 56
- •4.1. Необхідна умова існування екстремуму функції двох змінних .............. 76
4.3. Приклади та задачі для самостійної роботи.
Знайти екстремуми функцій двох змінних:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ,
якщо
,
якщо
![]() ,
,
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ,
якщо
,
;
,
якщо
,
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ,
,
![]() ;
;
15)
![]() ,
,
![]() ;
;
16)
![]() ,
;
,
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
![]() ;
;
24)
![]() ;
;
25)
![]() ;
;
26)
![]() ;
;
27)
![]() ;
;
28)
![]() ;
;
29)
![]() ;
;
30)
![]()
![]() .
.
4.4 Умовні екстремуми функції двох змінних
1.
При відшуканні найбільшого і найменшого
значень функції двох змінних часто
виникають задачі, зв'язані зі знаходженням
так званого умовного екстремуму. Це
завдання полягає в тім, щоб на лінії
![]() ,
що належить області визначення функції
,
знайти точку
,
у якій значення функції є найбільшим
чи найменшим в порівнянні зі значеннями
цієї функції в точках лінії
,
що знаходяться в деякому околі точки
.
Така
точка
називається
точкою
умовного екстремуму,
а значення функції
в ній
називається
умовним екстремумом.
,
що належить області визначення функції
,
знайти точку
,
у якій значення функції є найбільшим
чи найменшим в порівнянні зі значеннями
цієї функції в точках лінії
,
що знаходяться в деякому околі точки
.
Така
точка
називається
точкою
умовного екстремуму,
а значення функції
в ній
називається
умовним екстремумом.
Потрібно зазначити, що на відміну від звичайної точки екстремуму, значення функції порівнюється зі значеннями функції не в усіх точках деякого її околу, а тільки в тих, які належать лінії .
Зрозуміло також, що точка звичайного екстремуму функції є точкою умовного екстремуму для довільної лінії, що проходить через цю точку. Але зворотне твердження невірне: точка умовного екстремума не обов'язково є точкою звичайного екстремуму.
Наприклад,
функція
![]() має
максимум, що дорівнює 1, в
початку координат, а на лінії
має
максимум, що дорівнює 1, в
початку координат, а на лінії
![]() ця функція має умовний екстремум
(максимум) у точці
ця функція має умовний екстремум
(максимум) у точці
![]() .
.
Графік функції зображений на рисунку 20.
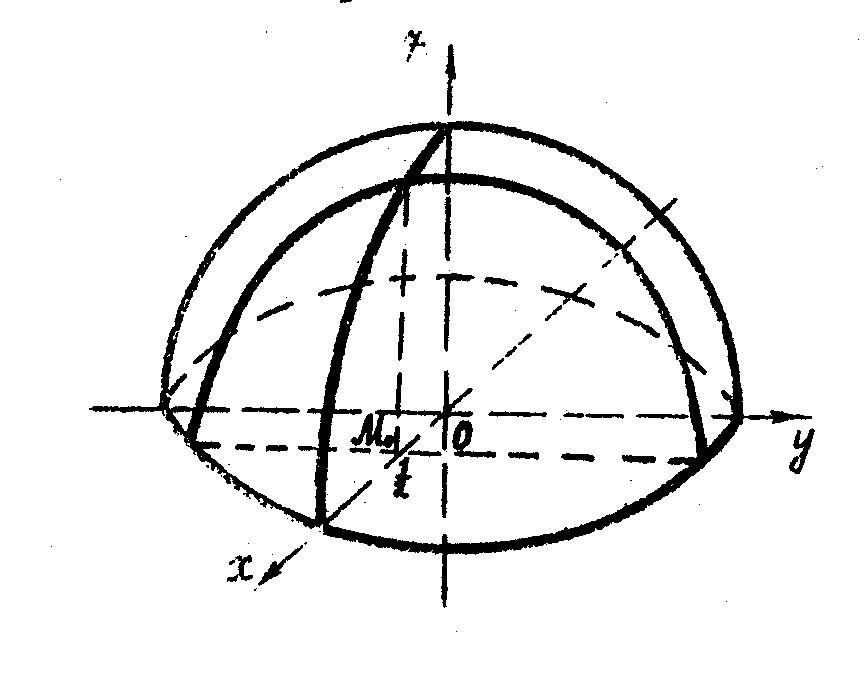
Рис.20
2. Розглянемо методи знаходження умовних екстремумів диференційовної функції для різних способів задання рівняння лінії (так званого рівняння зв'язку), у точках якої відшукується умовний екстремум.
Спочатку
розглянемо той випадок, коли лінія
задається рівнянням
![]() ,
де
,
де
![]() – диференційовна функція. У цьому
випадку підставимо в
замість
функцію
і одержимо функцію однієї змінної
– диференційовна функція. У цьому
випадку підставимо в
замість
функцію
і одержимо функцію однієї змінної
![]() .
Тим самим задача відшукування
умовних екстремумів
звелась до відшукування
екстремумів
функції однієї змінної. Знайшовши точки
екстремумів
.
Тим самим задача відшукування
умовних екстремумів
звелась до відшукування
екстремумів
функції однієї змінної. Знайшовши точки
екстремумів
![]() функції
і визначивши потім значення
функції
і визначивши потім значення
![]() з рівняння лінії
з рівняння лінії
![]() ,
одержимо точки
,
одержимо точки
![]() умовних екстремумів функції
.
умовних екстремумів функції
.
Досить просто розв’язується також задача знаходження умовних екстремумів у випадку, коли лінія задана параметричними рівняннями:
![]()
![]() ,
,
де
![]() і
і
![]() - диференційовні функції. Підставивши
вирази для
та
у функцію
,
знову приходимо до задачі відшукування
екстремумів функції однієї змінної
- диференційовні функції. Підставивши
вирази для
та
у функцію
,
знову приходимо до задачі відшукування
екстремумів функції однієї змінної
![]() . Визначивши точки екстремумів цієї
функції і підставивши їхнє значення у
функції
. Визначивши точки екстремумів цієї
функції і підставивши їхнє значення у
функції
![]() ,
,
![]() ,
одержимо точки умовних екстремумів
функції
.
,
одержимо точки умовних екстремумів
функції
.
Більш
складною є задача знаходження умовних
екстремумів функції, коли рівняння
лінії задане в неявному виді
![]() .
У цьому випадку для відшукування умовних
екстремумів застосовується метод
множників Лагранжа.
.
У цьому випадку для відшукування умовних
екстремумів застосовується метод
множників Лагранжа.
Теорема
8. Якщо
диференційовна функція
має умовний екстремум у точці
лінії
,
і
визначає неявну диференційовну функцію
,
що залежить від змінної
в околі точки
![]() ,
то існує таке число
,
то існує таке число
![]() ,
що частинні похідні функції
,
що частинні похідні функції
![]() в точці
дорівнюють нулю.
в точці
дорівнюють нулю.
Доведення. Так як за умовою теореми рівняння зв'язку визначає неявну функцію від змінної , то функція є складеною функцією, що залежить від . Повна похідна від цієї функції по дорівнює:
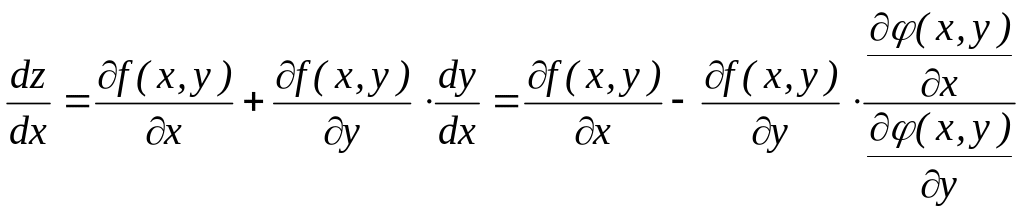 ,
,
де
похідна
![]() знайдена
за правилом
диференціювання
неявної
функції.
У точках
умовних екстремумів похідна
знайдена
за правилом
диференціювання
неявної
функції.
У точках
умовних екстремумів похідна
![]() дорівнює
нулю, отже
одержуємо одне рівняння,
що зв'язує
і
дорівнює
нулю, отже
одержуємо одне рівняння,
що зв'язує
і
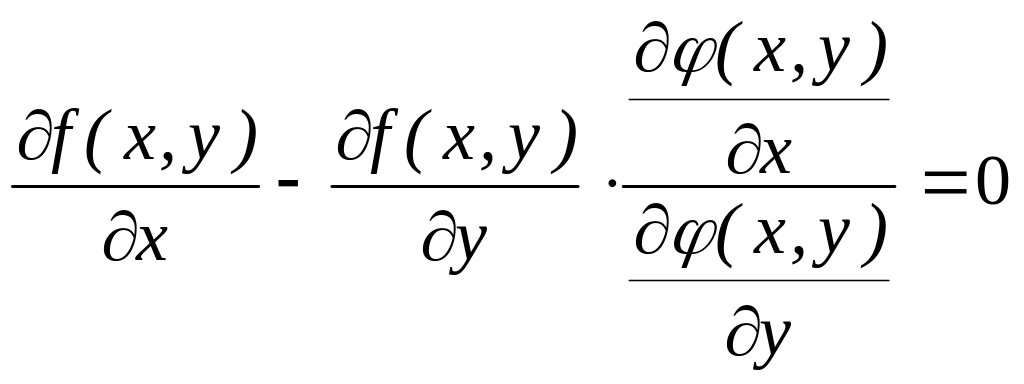 .
.
Перетворимо
це рівняння, поклавши в шуканій точці
умовного екстремуму
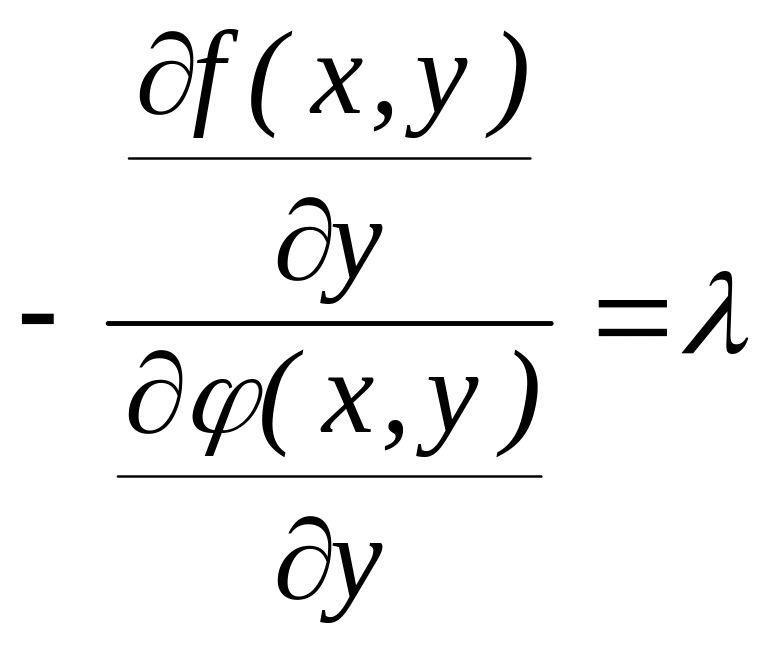 ,
де
- деяке невідоме число;
,
де
- деяке невідоме число;
маємо
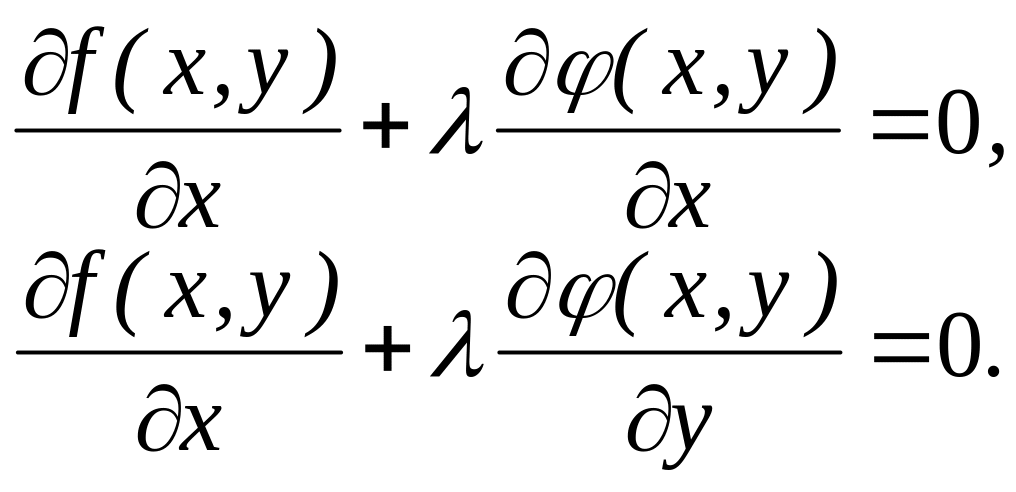 (4.1)
(4.1)
Приєднавши
рівняння зв'язку
до цих двох рівнянь, одержимо систему
трьох рівнянь із трьома невідомими
![]() .
Теорема доведена.
.
Теорема доведена.
Висновок. Відзначимо, що доведена теорема дає тільки необхідну умову існування умовного екстремуму. При розв’язуванні системи рівнянь (4.1) разом з рівнянням зв'язку визначаються координати точок, підозрюваних на умовний екстремум. Дуже часто зміст задачі чи вид досліджуваної функції в кожній конкретній ситуації допомагає встановити, чи є критична точка, підозрювана на умовний екстремум, точкою умовного екстремуму.
Достатні
умови існування умовного екстремуму
зв'язані з дослідженням знака визначника
третього порядку, складеного з частинних
і змішаних похідних другого порядку
по змінних
функції
![]() ,
обчислених у точці
,
обчислених у точці
![]() ,
що знайдена з рівняння (4.1)
і рівняння зв'язку
.
Сформулюємо ці умови.
,
що знайдена з рівняння (4.1)
і рівняння зв'язку
.
Сформулюємо ці умови.
Теорема 9. Якщо визначник
![]()
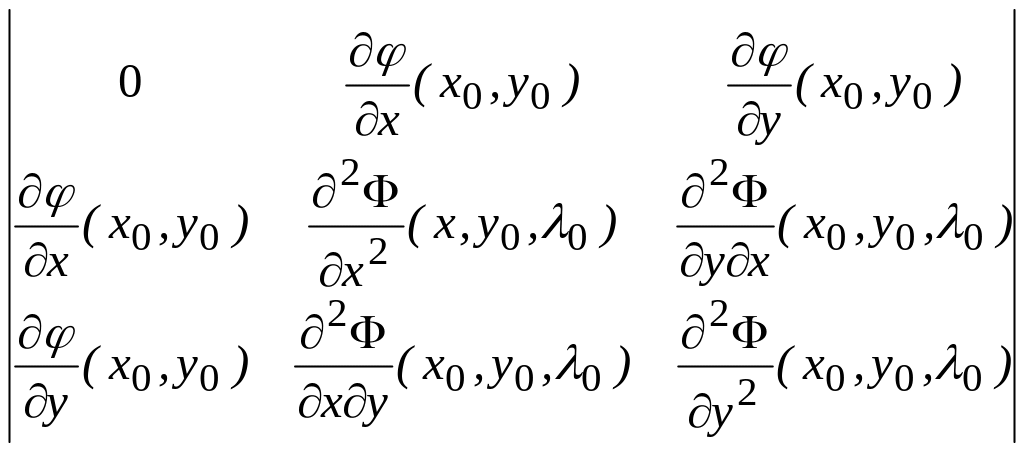
додатний,
то у функції
існує в точці
умовний максимум, якщо
![]() ,
то існує
умовний мінімум.
,
то існує
умовний мінімум.
Приклад
26.
Знайти умовний екстремум функції
![]() на прямій
на прямій
![]() .
.
Розв’язування. Виразимо через з рівняння зв'язку і підставимо цей вираз у задану функцію; маємо
![]() .
.
Далі
знаходимо похідну
![]() і прирівнюємо її до
нуля:
і прирівнюємо її до
нуля:
![]() .
.
Розв’язавши
одержане рівняння, знаходимо його
корінь:
![]() .
.
Так
як
![]() для
для
![]() і
і
![]() ,
коли
,
коли
![]() ,
то функція
,
то функція
![]() має в точці
максимум. З цього випливає,
що у функції
існує в точці з координатами
,
має в точці
максимум. З цього випливає,
що у функції
існує в точці з координатами
,
![]() умовний максимум на прямій
,
який дорівнює
умовний максимум на прямій
,
який дорівнює
![]() .
.
Приклад
27.
Знайти умовний екстремум функції
![]() на параболі
на параболі
![]() .
.
Розв’язування.
Спочатку з рівняння параболи знаходимо
![]() .
Підставивши
цей
вираз для
у функцію
,
одержуємо функцію, що залежить від
однієї змінної
:
.
Підставивши
цей
вираз для
у функцію
,
одержуємо функцію, що залежить від
однієї змінної
:
![]() .
.
Потім знаходимо похідну і прирівнюємо до нуля:
![]() .
.
Звідси
![]() .
Досліджуємо ці точки на екстремуми:
якщо
.
Досліджуємо ці точки на екстремуми:
якщо
![]() ,
то
,
то
![]() ,
якщо
,
якщо
![]() ,
то
,
то
![]() ,
і коли
,
і коли
![]() ,
.
,
.
Таким
чином, у функції
![]() існує в точці
існує в точці
![]() мінімум, а в точці
мінімум, а в точці
![]() максимум. Отже, функція
в точці з координатами
,
максимум. Отже, функція
в точці з координатами
,
![]() має умовний мінімум, а в
точці
з координатами
,
– умовний максимум на параболі
має умовний мінімум, а в
точці
з координатами
,
– умовний максимум на параболі
![]() .
При цьому
.
При цьому
![]() ,
,
![]() .
.
Приклад
28.
Знайти умовні екстремуми функції
![]() на колі
на колі
![]()
Розв’язування.
Підставимо значення
![]() ,
,
![]() у функцію
у функцію
![]() ,
в результаті одержуємо функцію однієї
змінної. Наша задача звелася до
знаходження екстремумів функції
,
в результаті одержуємо функцію однієї
змінної. Наша задача звелася до
знаходження екстремумів функції
![]() на інтервалі
на інтервалі
![]() .
Узявши похідну по
.
Узявши похідну по
![]() і прирівнявши її до нуля, знаходимо
«стаціонарні» точки функції
і прирівнявши її до нуля, знаходимо
«стаціонарні» точки функції
![]() :
:
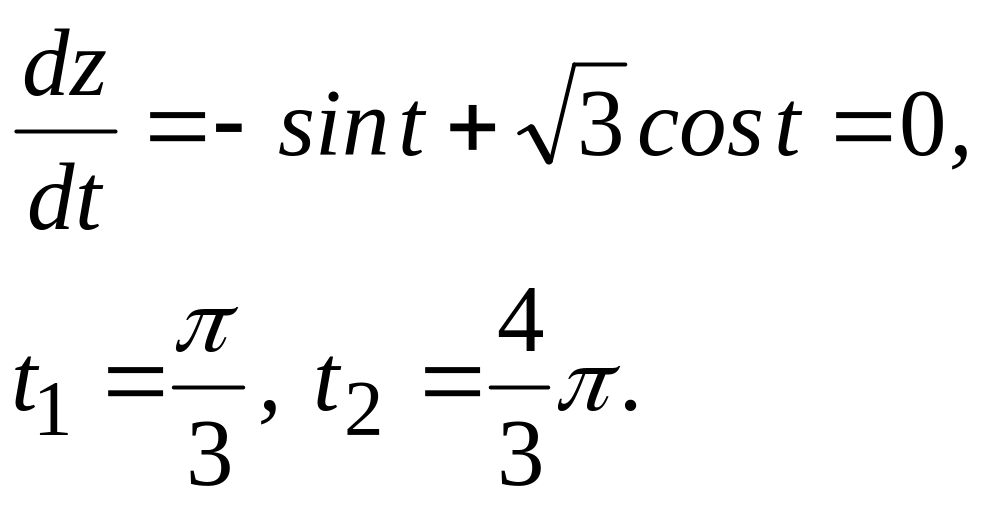
Досліджуємо
ці точки на екстремум: якщо
![]() ,
то
,
то
![]() ,
для
,
для
![]()
![]() і коли
і коли
![]() ,
,
тобто функція
в точці
,
,
тобто функція
в точці
![]() має максимум, а в точці
має максимум, а в точці
![]() – мінімум. Тоді у функції
– мінімум. Тоді у функції
![]() існує в точці з координатами
існує в точці з координатами
![]() ,
,
![]() умовний максимум
умовний максимум
![]() ,
а в точці з координатами
,
а в точці з координатами
![]() ,
,
![]() умовний мінімум
умовний мінімум
![]() на колі
на колі
Приклад
29.
Знайти умовні екстремуми функції
![]() на колі
на колі
![]() .
.
Розв’язування. Складемо функцію
![]()
і відшукаємо її стаціонарні точки, прирівнявши нулю її перші частинні похідні:
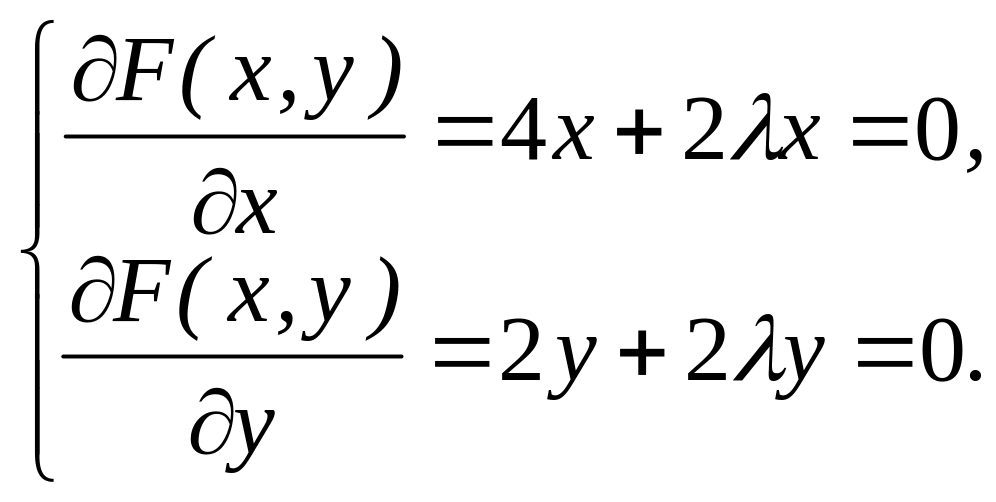 (4.2)
(4.2)
До отриманих рівнянь приєднаємо ще рівняння зв'язку
(4.3)
і розв’яжемо їх сумісно.
Якщо
число
![]() і
і
![]() ,
то з рівнянь (4.2)
випливає
,
то з рівнянь (4.2)
випливає
![]() ,
що суперечить умові (4.3).
При
,
що суперечить умові (4.3).
При
![]() з другого рівняння (4.2)
випливає, що
,
а з рівняння (4.3)
знаходимо
з другого рівняння (4.2)
випливає, що
,
а з рівняння (4.3)
знаходимо
![]() ;
при
;
при
![]() знаходимо
,
знаходимо
,
![]() .
Таким чином, точками умовного екстремуму
можуть бути точки
.
Таким чином, точками умовного екстремуму
можуть бути точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
З виду функції
робимо висновок, що в точках
і
функція
має умовний максимум
,
а в точках
і
- умовний мінімум
.
З виду функції
робимо висновок, що в точках
і
функція
має умовний максимум
,
а в точках
і
- умовний мінімум
![]() .
Дійсно, рухаючись
по колу від
і
,
ми збільшуємо значення функції, а
рухаючись
від точок
і
по колу, зменшуємо значення функції.
.
Дійсно, рухаючись
по колу від
і
,
ми збільшуємо значення функції, а
рухаючись
від точок
і
по колу, зменшуємо значення функції.
Приклад
30.
Знайти умовний максимум функції
![]() ,
якщо змінні
,
якщо змінні
![]() додатні і задовольняють рівняння
додатні і задовольняють рівняння
![]() .
.
Розв’язування. Складемо допоміжну функцію
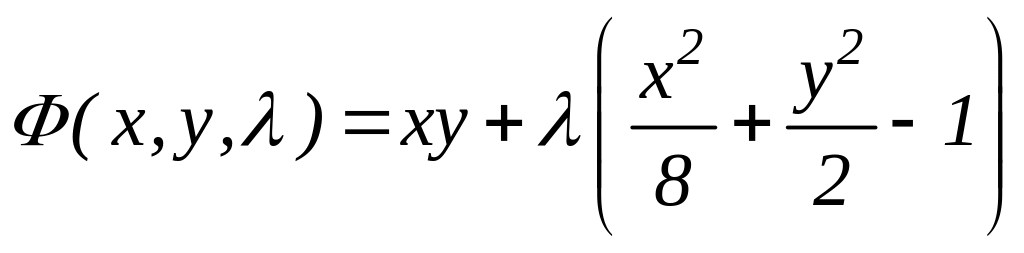 .
.
Прирівнюючи частинні похідні до нуля, маємо
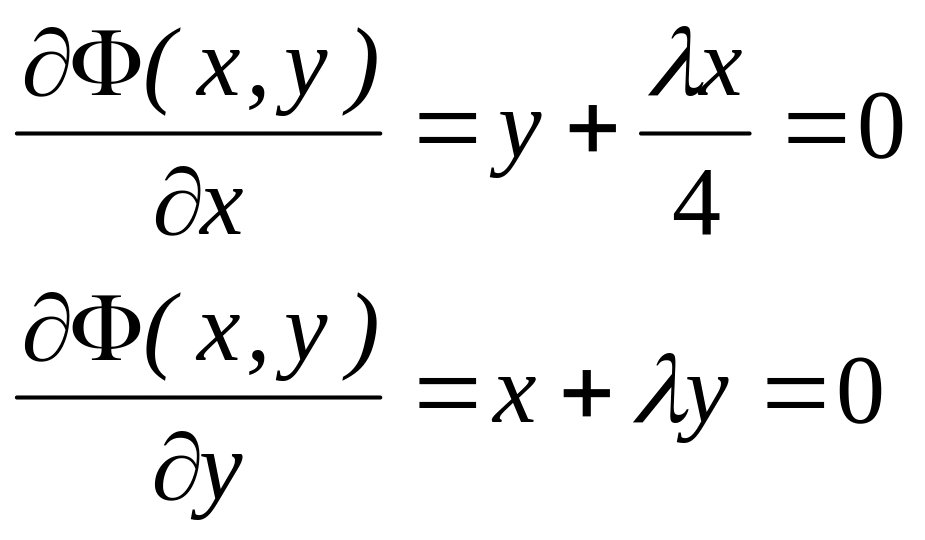
Виключаємо з цих рівнянь параметр і одержуємо
![]() .
.
Розв’язуючи
це рівняння разом з рівнянням
і враховуючи те, що
![]() ,
знаходимо
,
знаходимо
![]() .
Далі визначаємо значення параметра
у випадку, коли
.
Далі визначаємо значення параметра
у випадку, коли
![]() ,
і частинні та змішані похідні другого
порядку функції
,
і частинні та змішані похідні другого
порядку функції
![]() :
:
![]()
![]() ,
,
![]()
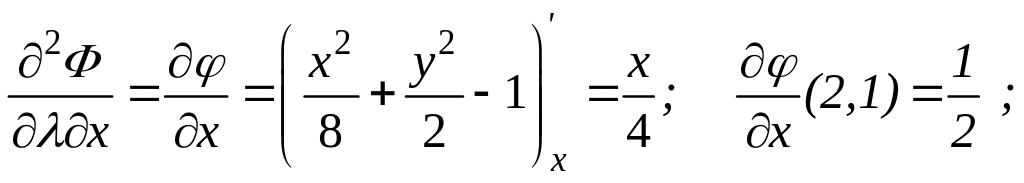
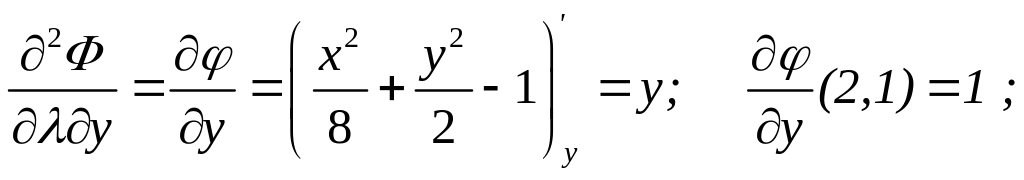
![]() .
.
Cкладаємо та обчислюємо визначник
 =
=
![]()
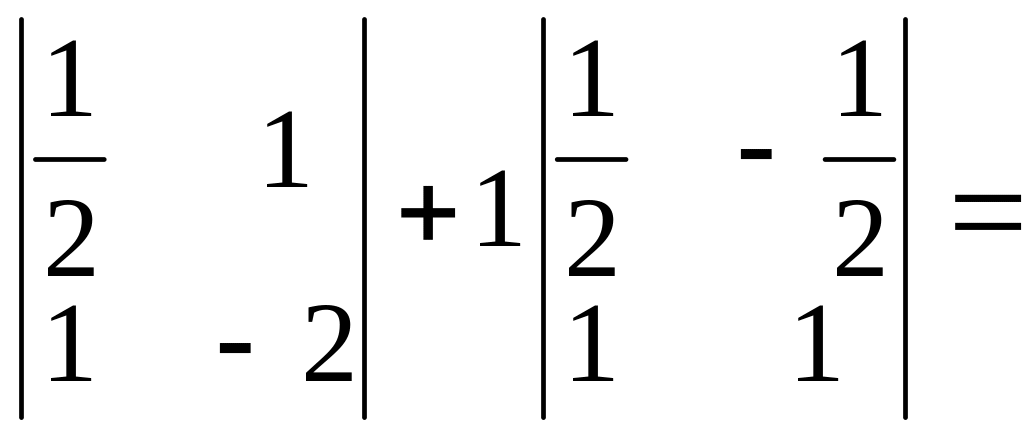
![]() (–1–1)+1
(–1–1)+1![]()
![]() =1+1=2.
=1+1=2.
Так
як визначник додатний
(![]() =2), то відповідно до теореми 9,
у функції існує в точці
=2), то відповідно до теореми 9,
у функції існує в точці
![]() умовний максимум.
умовний максимум.
