Далі розглянемо способи знаходження екстремумів функції двох змінних.
4.1. Необхідна умова існування екстремуму функції двох змінних.
Установимо
спочатку необхідні умови існування в
точці
максимуму
або
мінімуму
функції.
Теорема
6.
Якщо у функції
існують частинні похідні першого порядку
в точці екстремуму
,
то ці частинні похідні дорівнюють нулю:
,
.
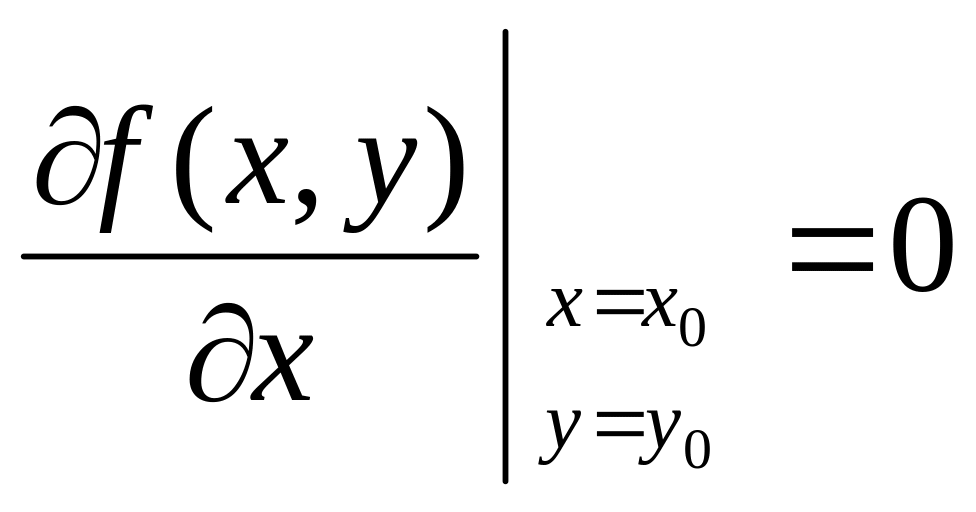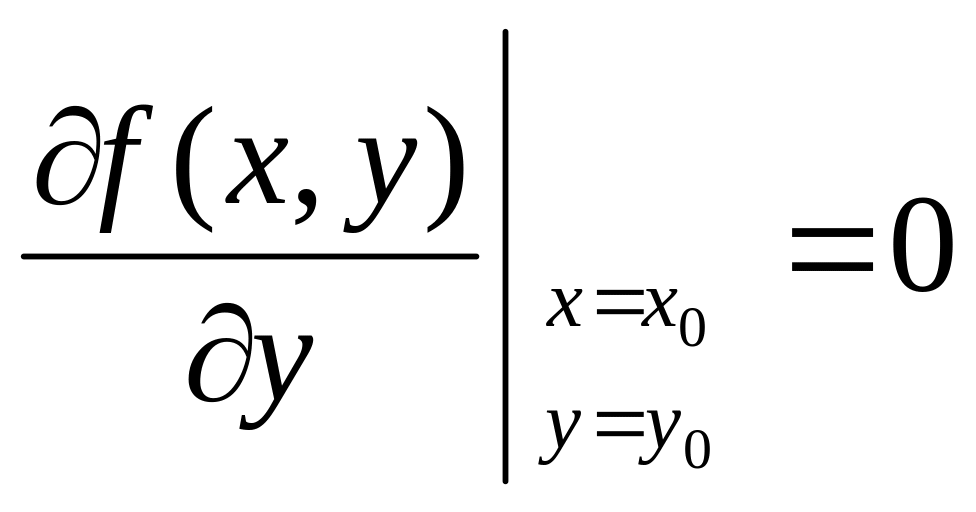Доведення.
Нехай
має в точці
екстремум.
Розглянемо функцію
при
як
функцію однієї
змінної
.
З
визначення екстремуму функції
випливає, що
функція
,
як функція однієї змінної, досягає
экстремуму
при
.
Крім того, функція
має похідну в точці
,
що дорівнює
.
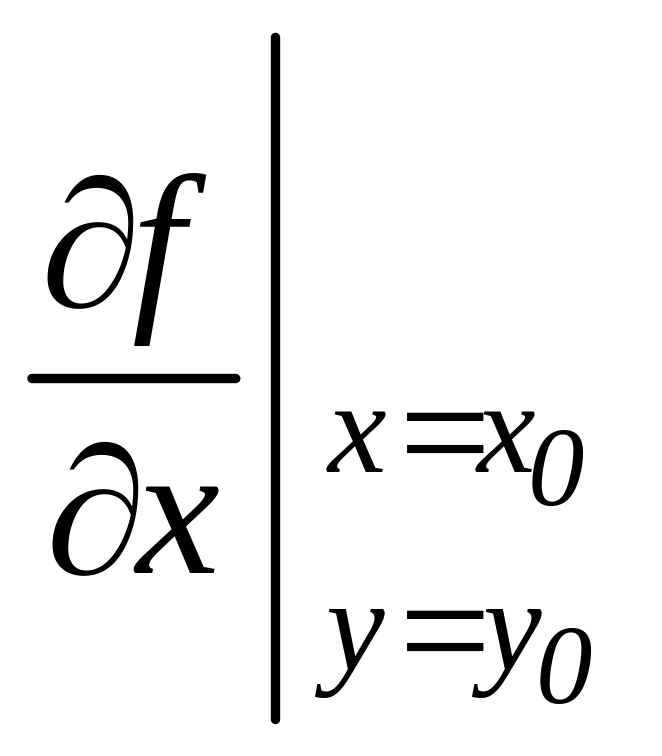Як відомо, необхідною умовою існування
екстремуму диференційовної функції
однієї змінної
є рівність нулю похідної в точці
,
тобто
.
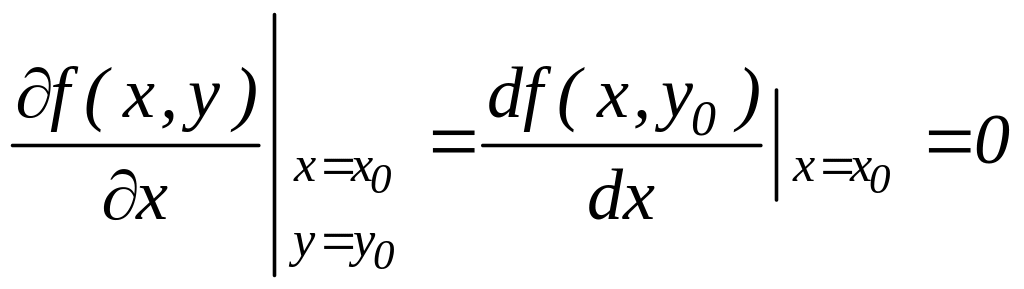Аналогічно,
функція
,
як функція однієї змінної
,
досягає екстремуму
в точці
.
Виходить,
,
що і потрібно було довести.
Таким чином, рівність нулю частинних похідних першого порядку функції (якщо вони існують) є необхідною умовою існування экстремуму в точці.
Приклад
19.
Функція
визначена і диференційовна в усіх точках
площини. В початку координат функція
досягає мінімуму і її частинні похідні
,
в
точці
дорівнюють нулю.
Графік функції зображений на рисунку 16.
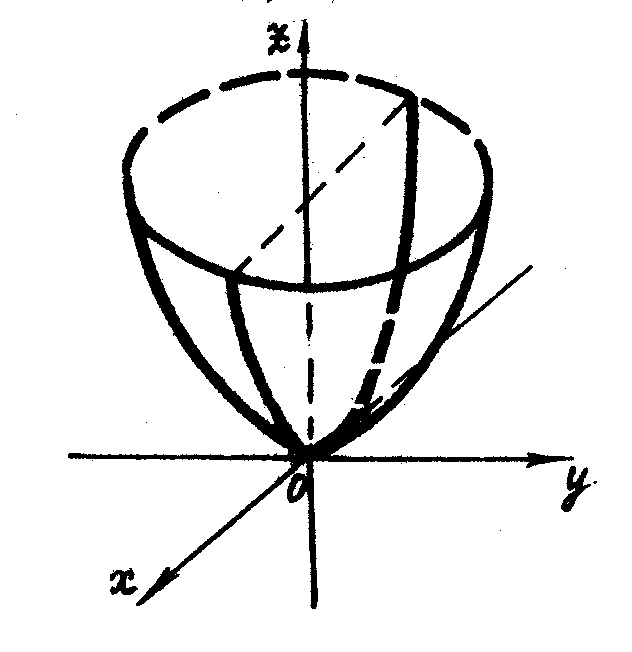
Рис.16
Можна дати наступну геометричну ілюстрацію доведеної вище необхідної ознаки існування екстремуму.
Якщо
має в точці
екстремум і існує дотична площина до
поверхні – графіка функції в точці
,
то ця дотична площина паралельна площині
незалежних змінних (площині
).
Це випливає з того, що рівняння дотичної
площини
до
поверхні
для екстремальної точки
за теоремою 6 приймає вигляд:
.
Отримане рівняння є рівнянням
площини, паралельної площині
.
Приклад
20.
Функція
визначена і неперервна на множині
.
У точці
функція досягає максимуму, який дорівнює
5, частинні похідні функції в цій точці
дорівнюють нулю. Дотична площина у
відповідній точці
паралельна площині
,
її рівняння
.
Графік функції зображений на рисунку 17.
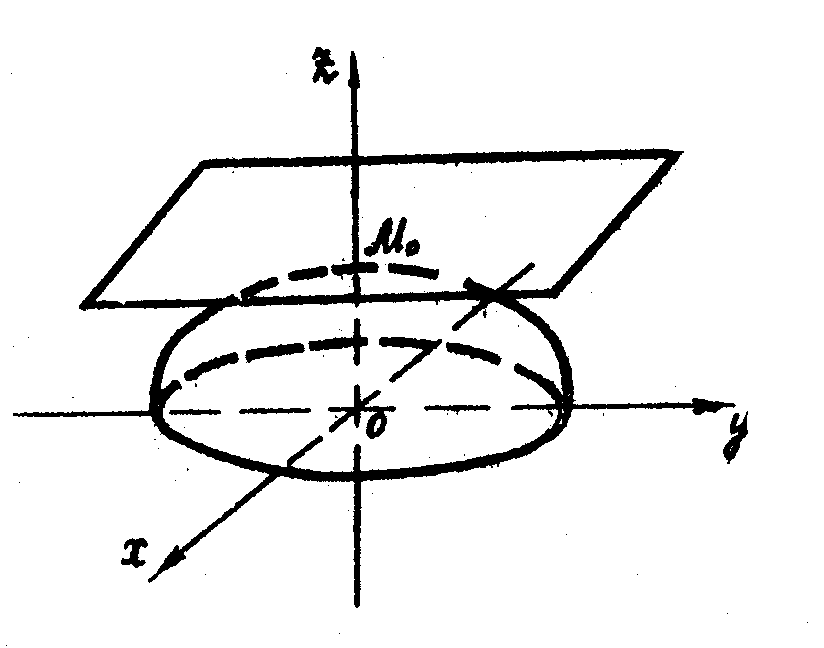
Рис.17
Далі відзначимо, що неперервна функція може мати екстремум і в тих точках, де хоча б одна з частинних похідних першого порядку не існує.
Приклад
21.
Функція
визначена і неперервна на всій площині.
У точці
функція досягає мінімуму і дорівнює
нулю, але частинні похідні функції в
цій точці не існують.
Графік функції зображений на рисунку 18.
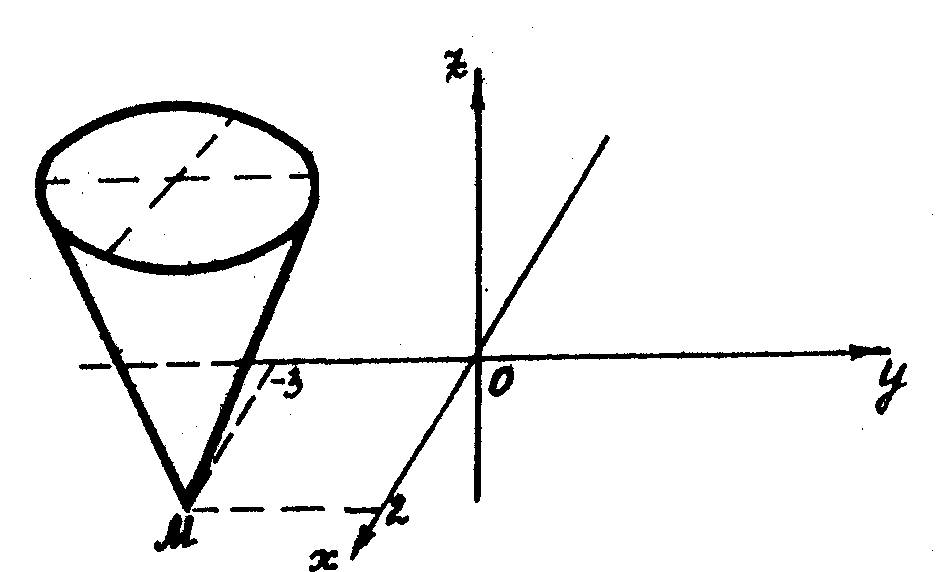
Рис.18
З
вищесказаного випливає,
що необхідною ознакою існування
екстремуму
функції в точці
є або рівність нулю частинних похідних
першого порядку, якщо
вони існують, або,
щоб хоч би
одна з цих похідних не існувала.
Точки, в яких виконуються ці умови, називаються критичними.
Так
само, як і для функції однієї змінної,
ці умови не є достатніми. Якщо, наприклад,
узяти функцію
,
то для неї частинні похідні
і
дорівнюють одночасно нулю в початку
координат
;
у цій точці
.
З виду функції ясно, що в будь-якому
околі точки
функція приймає як додатні, так і від'ємні
значення, тобто екстремуму
в цій точці немає.
Графік функції (гіперболічний параболоїд) зображений на рисунку 19.
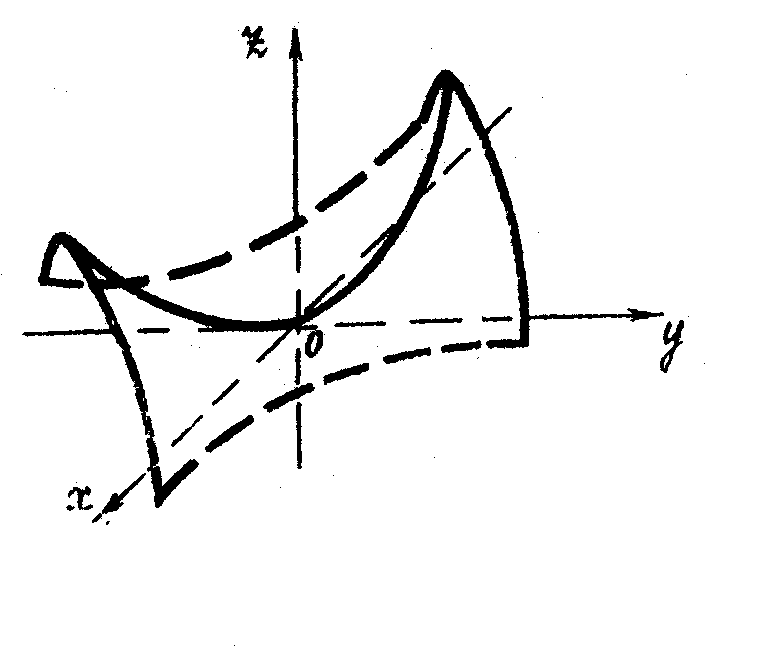
Рис.19