3.2.2. Приклади для самостійної роботи.

Знайти екстремуми функцій однієї змінної:

1)

2)

3)

4) , якщо

5)

6)

7)

8)

9) , якщо

10)

11)

12)

13)

14) , якщо

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

27)

28)

29)

30)

3.2.3 Друга достатня умова існування екстремуму функції однієї змінної.

1. При знаходженні екстремумів функції, крім вищевикладеної достатньої умови, що використовує першу похідну досліджуваної функції, також застосовується достатня умова, що використовує другу похідну функції. Сформулюємо її.

Теорема 3. Нехай у критичній точці функція двічі диференційовна. Якщо при цьому , то є точкою максимуму, якщо ж , то – точка мінімуму.

Доведення. Нехай для визначенності у критичній точці . Доведемо, що є точкою мінімуму функції. За визначенням другої похідної маємо

.

Так як за умовою теореми і , то

.

З властивості границі функції випливає, що для досить малих за абсолютною величиною приростів виконується нерівність:

.

Нехай , тоді <0, якщо ж , то >0. Таким чином, перша похідна при переході аргументу через критичну точку зліва направо змінює знак з мінуса на плюс. З раніше доведеної достатньої умови існування екстремума випливає, що має в точці мінімум.

Аналогічно доводиться існування максимума в точці , якщо .

Зауваження 1. Відзначимо, що для застосування теореми 3 на функцію накладаються більш сильні вимоги, чим в умові теореми 2, тому теорема 2 може бути застосована в випадках, коли умови теореми 3 не виконуються. Але в багатьох задачах застосування достатньої умови, що використовує знак другої похідної, прискорює знаходження екстремумів.

Розглянемо приклади, при розв'язуванні яких застосовується теорема 3.

Приклад 8. Знайти екстремуми функції

.

Розв'язування. Область визначення функції – уся числова пряма. Знаходимо похідні:

, .

Далі прирівнюємо першу похідну до нуля і з одержаного рівняння знаходимо критичні точки , . У точці маємо , а . За теоремою 3 функція має в точці мінімум і в точці – максимум. При цьому

і

.

Приклад 9. Знайти екстремуми функції , заданої на сегменті .

Розв'язування. Обчислюємо першу і другу похідні функції:

, .

Прирівнюючи нулю першу похідну, знаходимо критичні точки функції на інтервалі .

; , .

Далі маємо: , . Отже, у точці функція досягає мінімуму:

,

а у точці - максимуму:

.

Зауваження 2. Далі відзначимо, що теорема 3 у випадку, коли і , не дозволяє визначити чи має функція екстремум у точці . Цих умов просто недостатньо для такого визначення, тому що при виконанні умов можливі випадки наявності екстремуму і випадки відсутності.

Так, наприклад, перша і друга похідні розглянутої в 3.1 функції в точці дорівнюють нулю, і екстремум в цій точці відсутній.

Для функції (рисунок 10) похідні і дорівнють нулю в точці , а функція має в цій точці мінімум.

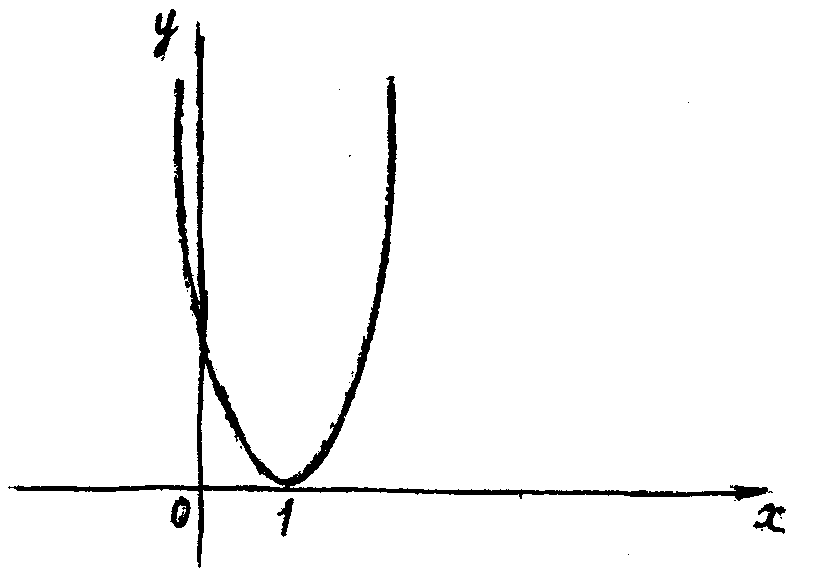
Рис.10

2. Далі сформулюємо і доведемо теорему, що доповнює теорему 3.

Теорема 4. Нехай у критичній точці у функції існує похідна порядку і , а . Якщо ­ - парне, то функція має в точці екстремум, саме, якщо – мінімум, і у випадку, коли – максимум. При непарному – екстремуму немає.

Доведення. Якщо , то це теорема 3. Нехай ,тоді і . За визначенням похідної -го порядку маємо:

.

Так як за умовою теореми , то за властивістю границі для досить малих за абсолютною величиною виконується нерівність .

Отже, якщо , то , а якщо , то , тобто праворуч від додатня на деякому проміжку . Так як похідна ( )-го порядку за визначенням є похідною від , то за зауваженням 2 до теореми 2 спадає на інтервалі і зростає для . З умови випливає, що ліворуч і праворуч від додатня.

Зокрема, коли , то і функція в силу зауваження 1 до теореми 2 не досягає екстремуму в точці .

Застосовуючи в випадку аналогічні міркування для визначення знака потрібне число разів, одержуємо:

1. знаки похідних , , … співпадають відповідно на інтервалах і 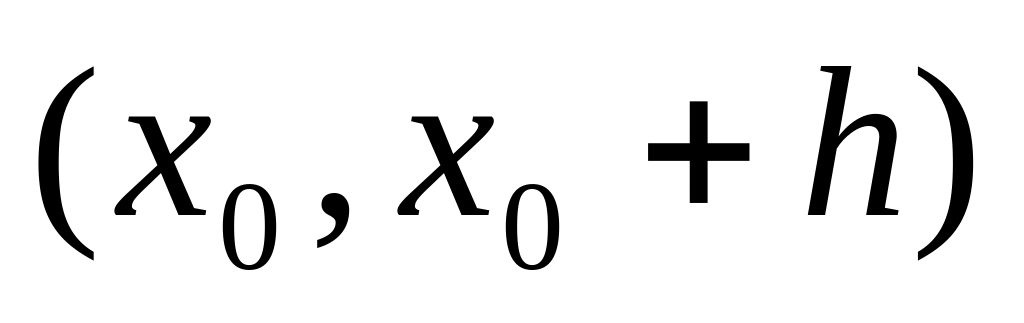; якщо , то похідні , , … від'ємні ліворуч від і додатні праворуч від ;

2. похідні , 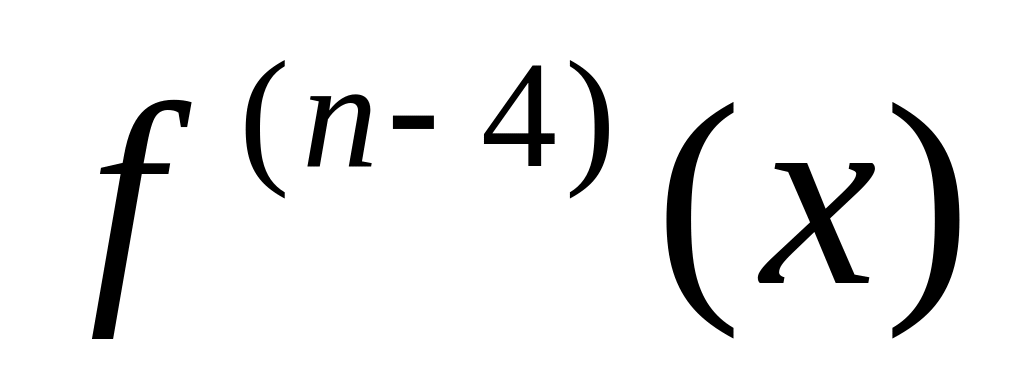, … мають однакові знаки (додатні, якщо ) в інтервалах і .

Оскільки при парному число – непарне, то від'ємна ліворуч від і додатня праворуч від . При непарному число – парне і як ліворуч, так і праворуч від у деякому інтервалі, якщо

Отже, за теоремою 2 при парному функція має в точці мінімум, а при непарному згідно із зауваженням 1 до теореми 2 екстремум в точці відсутній.

Доведення теореми у випадку, коли , аналогічне.

Зауваження. Відзначимо, що в умовах теореми 4 на функцію накладаються більш сильні вимоги, ніж в умовах теореми 2 і теореми 3. Але теорема 4 буває часто корисною в випадках, коли теорема 3 взагалі не застосовна , а застосування теореми 2 зв‘язане з труднощами визначення інтервалів монотонності першої похідної в околі стаціонарної точки.

Приклад 10. Знайти екстремуми функції .

Розв′язування. Функція визначена і нескінченно диференційовна на всій числовій осі. Її похідні

, ,

перетворюються в нуль в точці .

Так як для будь-яких дійсних чисел , у тому числі і для , то функція має мінімум у точці рівний 2.

Інших екстремумів у цієї функції не існує, тому що друга похідна

для всіх і, отже, перша похідна зростає і перетворюється в нуль лише в точці .

Графік функції зображений на рисунку11.

Рис.11