63

Частина 2. Екстремуми функцій однієї та двох змінних

Глава 3. Екстремуми функції однієї змінної

Розглянемо графік деякої неперервної функції, зображеної на рис. 1.

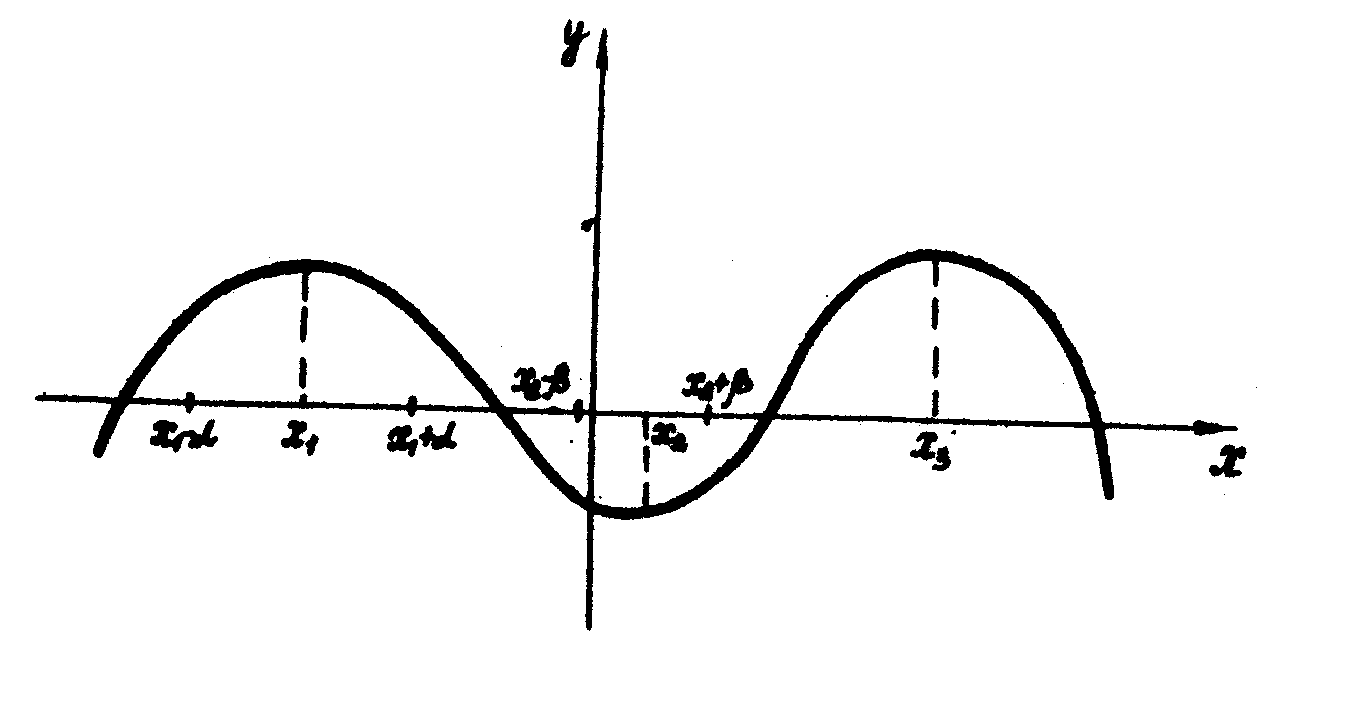
Рис.1

З рисунка видно, що в точці значення функції більше значень функції у всіх «сусідніх» точках як ліворуч, так і праворуч, тобто в точках з деякого околу точки . У цьому випадку кажуть, що в точці функція має максимум.

Визначення 1. Функція має в точці максимум, якщо існує такий окіл точки , що для кожного з цього околу виконується нерівність

.

У точці (на рис.1) значення функції менше її значень в «сусідніх» точках з деякого околу точки . У цьому випадку кажуть, що в точці функція має мінімум.

Визначення 2. Функція має в точці мінімум, якщо існує такий окіл точки , що для кожного з цього околу виконується нерівність

.

Точки , в яких функція має максимуми чи мінімуми називаються екстремальними точками. Значення функції в екстремальних точках називаються екстремальними значеннями функції, чи просто екстремумами.

Варто звернути увагу, що визначення понять максимуму і мінімуму носять локальний характер і допускають, що функція визначена не тільки в самій екстремальній точці, але в деякому (нехай навіть дуже малому) околі цієї точки.

У зв'язку з цим варто чітко розрізняти дві задачі:

1) знайти екстремуми заданої функції ;

2. знайти найбільше або найменше значення функції на деякій множині точок з області її визначення.

Перша з цих задач означає, що з області визначення функції потрібно знайти всі екстремальні точки й обчислити значення . Друга задача означає, що з усіх значень функції на заданій множині варто відшукати те значення, яке більше всіх інших, або менше всіх інших її значень. Надалі мінімум функції будемо позначати , а максимум - .

Приклад 1. Функція

зображена на рисунку 2.

Як видно з рисунку, функція має в точці мінімум, що дорівнює 0, а найменше значення функції має в точці ; при цьому

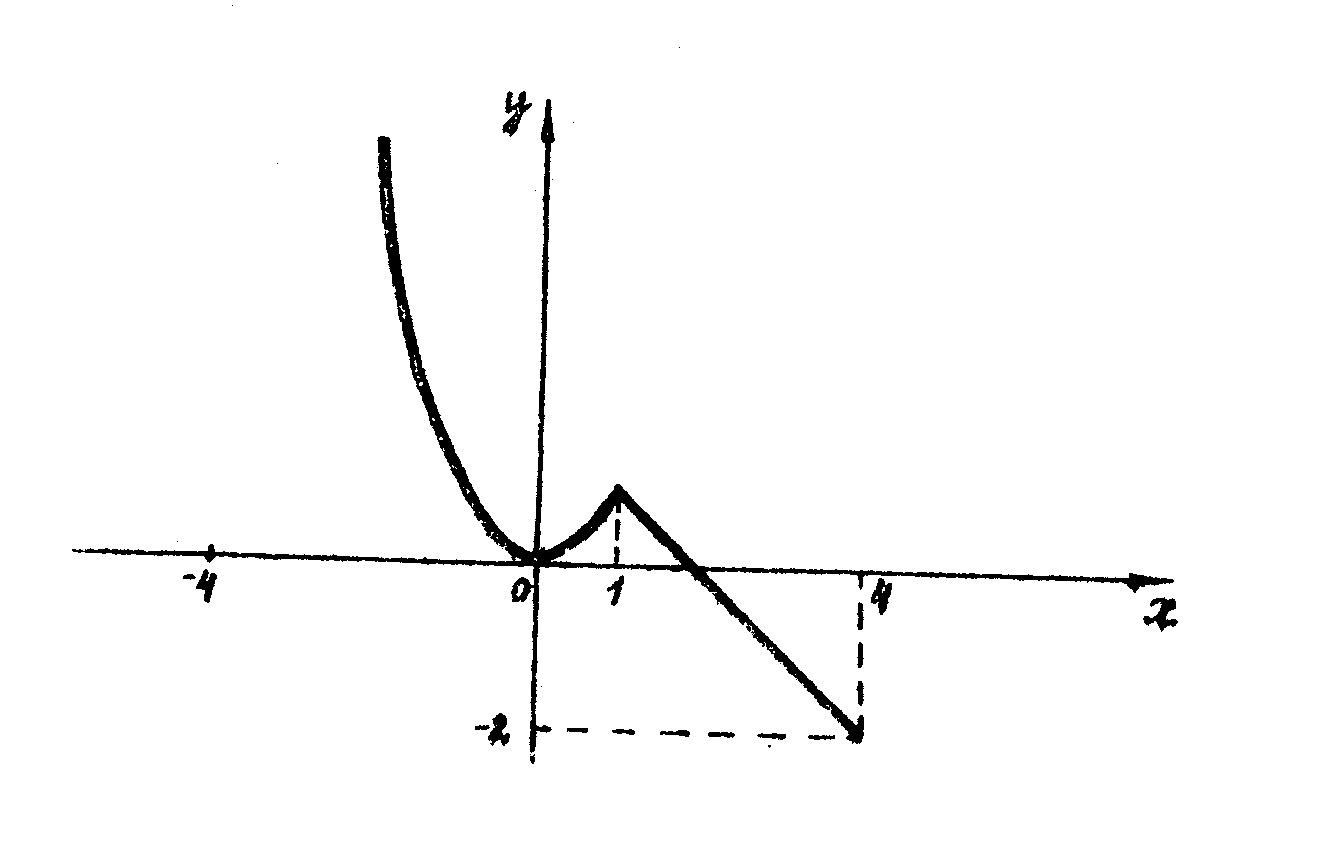
Рис.2

Задача знаходження екстремумів функції, якщо користуватися тільки їх визначенням, є дуже важкою й у більшості випадків практично не може бути розв'язаною. Тому потрібні ознаки, що дозволяли б швидко й ефективно знаходити екстремуми конкретних функцій.

3.1 Необхідна умова існування екстремуму функції однієї змінної

1. Допустимо спочатку, що в точці функція приймає екстремальне значення і в цій точці екстремуму існує скінченна похідна. У цьому випадку вірне наступне твердження.

Теорема 1. Якщо диференційовна в точці функція має в цій точці екстремум, то її похідна .

Доведення проведемо, наприклад, для випадку, коли функція приймає в точці максимальне значення. Тоді, за визначенням максимуму функції, існує такий окіл точки , що для всіх точок з цього околу

,

тобто

.

Звідси, якщо , то , і тому, в силу існування похідної в точці , маємо

. (3.1)

Якщо ж , то і, отже,

. (3.2)

Співвідношення (3.1) і (3.2) можуть виконуватися одночасно тільки в тім випадку, коли .

У такий же спосіб доводиться теорема і в випадку мінімуму функції.

Доведена теорема допускає просте геометричне тлумачення. З існування скінченної похідної в точці випливає, що графік функції має в точці дотичну, не паралельну осі Оу. Якщо ж функція досягає в точці екстремуму, то ця дотична паралельна осі Ох.

Приклад 2. Функція має мінімум у точці , який дорівнює 1 (рисунок 3). Похідна заданої функції в цій точці існує і, отже, дорівнює нулю. Дотична до графіка функції в точці паралельна осі Ох. Її рівняння . Так як , то рівняння дотичної є .

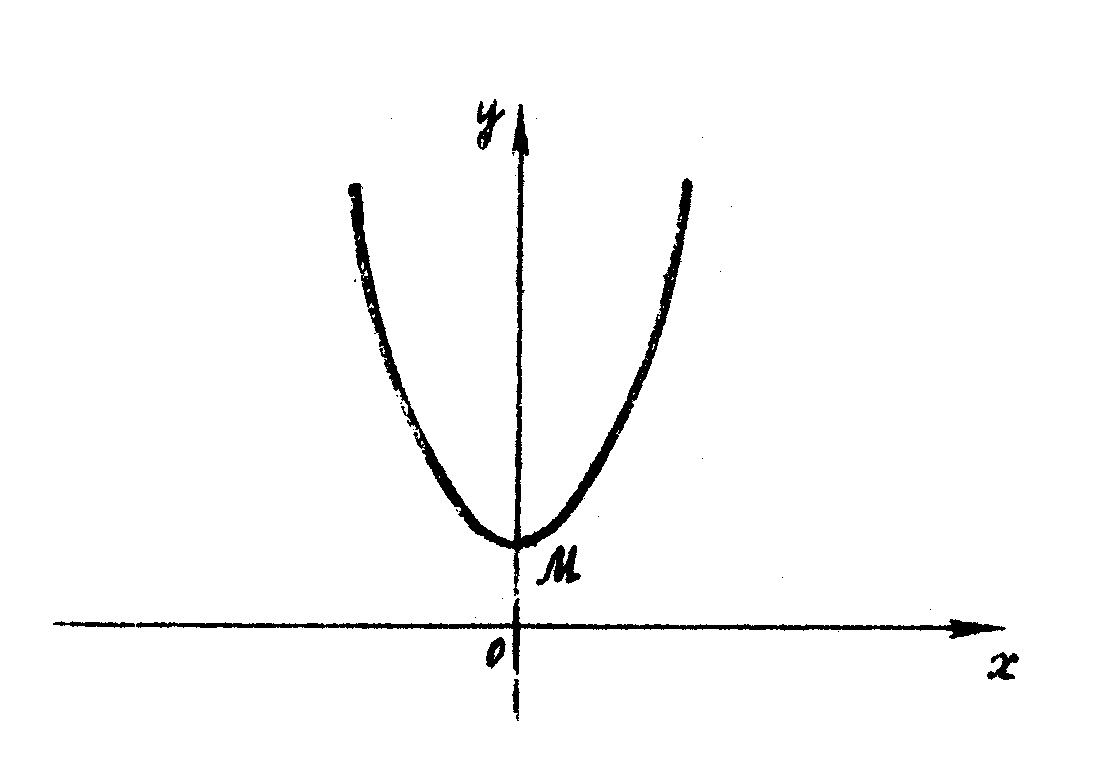
Рис.3.

2. До цього розглядався випадок, коли функція мала похідну в точці екстремуму. Однак можуть зустрітися випадки, коли в точках екстремуму не існує похідної. Розглянемо наступний приклад.

Приклад 3. У функції існує похідна в усіх точках числової осі, крім точки . Хоч в точці похідна не існує, але зрозуміло, що в цій точці функція має мінімум, тому що в інших точках своєї області визначення вона додатня. Графік функції зображений на рисунку 4.

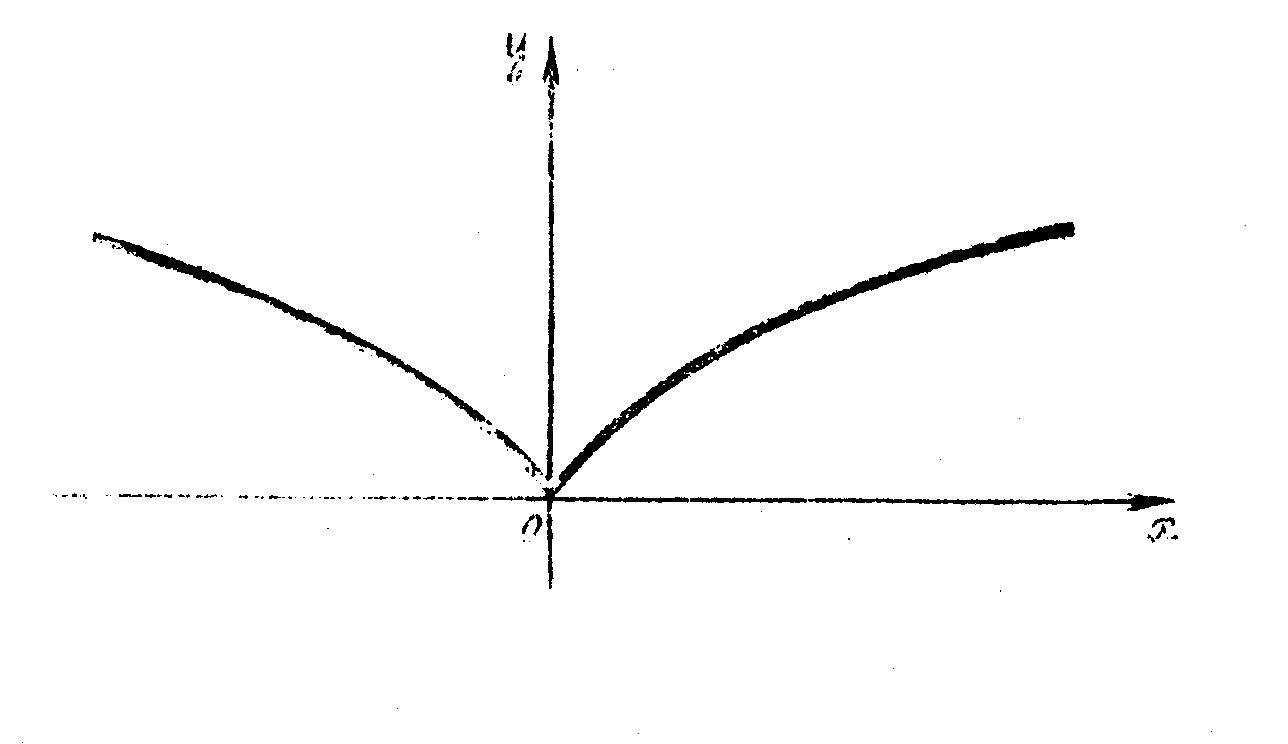
Рис.4.

Приклад 4. Нехай . Графік цієї функції зображений на рисунку 5. В точці у функції не існує похідної хоча б тому, що

,

а .

Однак очевидно, що в цій точці функція досягає максимуму.

Рис.5

Розглянуті приклади істотно доповнюють теорему 1.

Звідси випливає наступна необхідна ознака існування екстремуму:

якщо в точці неперервна функція досягає екстремуму, то її похідна в цій точці або існує і дорівнює нулю, або не існує.

Геометрично це означає, що графік неперервної функції в точці екстремуму або має дотичну, паралельну осі Ох (приклад 2) чи осі Оу (приклад 3), або зовсім не має дотичної (приклад 4).

Визначення 3. Точки, в яких похідна неперервної функції перетворюється в нуль або не існує, називаються критичними.

Необхідна ознака існування екстремуму вказує на той факт, що неперервна функція може досягати екстремального значення тільки в критичних точках. Але не треба думати, що в кожній критичній точці неперервна функція обов'язково має екстремум.

Так, наприклад, у функції в точці похідна дорівнює нулю, але екстремуму в цій точці функція не має. Графік функції зображений на малюнку 6.

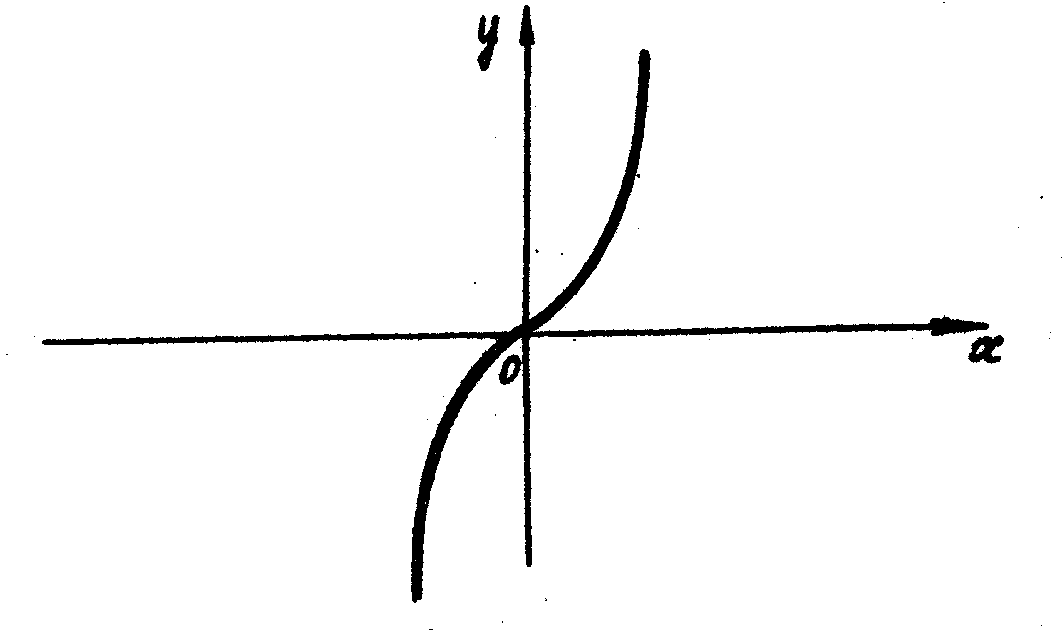
Рис.6.

Отже, для знаходження екстремумів функції надалі нам потрібні ознаки, за допомогою яких можна розпізнавати, чи має функція в критичній точці екстремум.