5.Теорема о распределении простых чисел
Теорема
о распределении простых чисел —
теорема аналитической
теории чисел,
описывающая асимптотику распределения
простых
чисел.
А именно, она утверждает, что функция
распределения простых чисел
(количество
простых чисел на отрезке от 1 до n) растёт
с ростом n как
,
то есть:
когда
Грубо
говоря, это означает, что у случайно
выбранного числа от 1 до n шанс оказаться
простым примерно равен
.
Также
эта теорема может быть эквивалентным
образом переформулирована для описания
поведения
-го
простого числа
:
она утверждает, что
(здесь
и далее запись
означает,
что
когда
аргумент функций стремится к бесконечности).
Более точно распределение простых чисел описывает функция интегрального логарифма. При справедливости гипотезы Римана верно[1]
5.1 История
Первым
статистическую закономерность в
расположении простых чисел подметил
Гаусс.
В письме Энке
(1849) он сообщил, что ещё в 1792 или 1793 году,
чисто эмпирически, обнаружил, что
плотность простых чисел «в среднем
близка к величине, обратно пропорциональной
логарифму»[2].
К этому времени, основываясь на таблицах
простых чисел, составленных Фелкелем
и Вегой,
Лежандр
предположил (в 1796 году), что функция
распределения простых чисел
(число
простых чисел, не превосходящих x)
может быть приближена выражением:
где
Гаусс
в упомянутом письме критикует формулу
Лежандра и, используя эвристические
рассуждения, предлагает другую
приближающую функцию — интегральный
логарифм:
Однако
Гаусс нигде не опубликовал эту гипотезу.
Оба приближения, как Лежандра, так и
Гаусса, приводят к одной и той же
предполагаемой асимптотической
эквивалентности функций
и
,
указанной выше, хотя приближение Гаусса
и оказывается существенно лучше, если
при оценке ошибки рассматривать разность
функций вместо их отношения.
В двух своих работах, 1848 и 1850 года, Чебышёв доказывает[3], что верхний M и нижний m пределы отношения
|
(1) |
заключены
в пределах
,
а также, что если
предел отношения (1) существует, то он
равен 1. Позднее (1881) Дж.
Дж. Сильвестр
сузил допустимый интервал для предела
с 10% до 4%.
В
1859 году
появляется работа Римана,
рассматривающая (введённую Эйлером
как функцию вещественного аргумента)
-функцию
в комплексной области, и связывающая
её поведение с распределением простых
чисел. Развивая идеи этой работы, в
1896 году
Адамар
и Валле-Пуссен
одновременно и независимо доказывают
теорему о распределении простых чисел.
Наконец, в 1949 году появляется не использующее комплексный анализ доказательство Эрдеша—Сельберга.
5.2 Переформулировка в терминах пси-функции Чебышёва
Общим начальным этапом рассуждений является переформулировка закона распределения простых чисел в терминах пси-функции Чебышёва, определяемой как
иными словами, пси-функция Чебышёва это сумма функции Мангольдта:
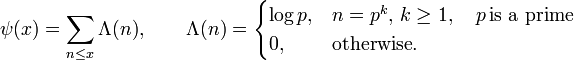
А именно, оказывается, что асимптотический закон распределения простых чисел равносилен тому, что
Это
происходит из-за того, что логарифм
«почти постоянен» на большей части
отрезка
,
а вклад квадратов, кубов, и т. д. в
сумму (*) пренебрежимо мал; поэтому
практически все складываемые логарифмы
примерно
равны
,
и функция
асимптотически
ведёт себя так же, как
.