4.Решето Эратосфена

Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому. Как и во многих случаях, здесь название алгоритма говорит о принципе его работы, то есть решето подразумевает фильтрацию, в данном случае фильтрацию всех чисел за исключением простых. По мере прохождения списка нужные числа остаются, а ненужные (они называются составными) исключаются.

Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000.

4.1 Алгоритм

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).

2. Пусть переменная p изначально равна двум — первому простому числу.

3. Зачеркнуть в списке числа от 2p до n считая шагами по p (это будут числа кратные p: 2p, 3p, 4p, …).

4. Найти первое незачеркнутое число в списке, большее чем p, и присвоить значению переменной p это число.

5. Повторять шаги 3 и 4, пока возможно.

Теперь все незачеркнутые числа в списке — это все простые числа от 2 до n.

На практике, алгоритм можно улучшить следующим образом. На шаге № 3 числа можно зачеркивать начиная сразу с числа p², потому что все составные числа меньше него уже будут зачеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда p² станет больше, чем n.^[2] Также, все p большие чем 2 — нечётные числа, и поэтому для них можно считать шагами по 2p, начиная с p².

4.2 Сложность алгоритма

Cложность алгоритма составляет операций при составлении таблицы простых чисел до ^[3].

Доказательство сложности

Для каждого простого будет выполняться внутренний цикл, который совершит действий. Следовательно, нужно оценить следующую величину:

=

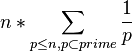
Так как количество простых чисел, меньше либо равных , оценивается как , и, как следствие, -е простое число примерно равно , то сумму можно преобразовать:

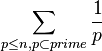
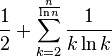
Здесь из суммы выделено первое простое число, чтобы избежать деления на нуль. Теперь следует оценить эту сумму интегралом:

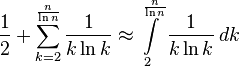
В итоге получается для изначальной суммы:

Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers»

4.3 Примеры реализаций

Множество примеров реализации приведено в проекте rosettacode.org^[7]. В данном разделе приводится несколько примеров на популярных языках программирования.

С/С++

int n;

vector<bool> prime (n+1, true);

prime[0] = prime[1] = false;

for (int i=2; i*i<=n; ++i) // valid for n < 46340^2 = 2147395600

if (prime[i])

for (int j=i*i; j<=n; j+=i)

prime[j] = false;

Java

import java.util.Arrays;

int n;

boolean[] primes=new boolean[n];

public void fillSieve() {

Arrays.fill(primes,true);

primes[0]=primes[1]=false;

for (int i=2;i<primes.length;i++) {

if(primes[i]) {

for (int j=2;i*j<primes.length;j++) {

primes[i*j]=false;

}

}

}

}

Python 2.x

Функция, возвращающая список простых чисел вплоть до заданного n:

def eratosthenes(n):

multiples = []

for i in xrange(2, n+1):

if i not in multiples:

print i

multiples.extend(xrange(i*i, n+1, i))

Haskell

primesTo n = eratos [2..n] where

eratos [] = []

eratos (p:xs) = p : eratos (xs `minus` [p*p, p*p+p..n])

minus (x:xs) (y:ys) = case (compare x y) of

LT -> x : minus xs (y:ys)

EQ -> minus xs ys

GT -> minus (x:xs) ys

minus xs _ = xs

4.4.Пример для n=30

Запишем натуральные числа начиная от 2 до 30 в ряд:

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Первое число в списке, 2 — простое. Пройдём по ряду чисел, зачёркивая все числа кратные 2 (то есть каждое второе, начиная с 2² = 4):

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Следующее незачеркнутое число, 3 — простое. Пройдём по ряду чисел, зачёркивая все числа кратные 3 (то есть каждое третье, начиная с 3² = 9):

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Следующее незачеркнутое число, 5 — простое. Пройдём по ряду чисел, зачёркивая все числа кратные 5 (то есть каждое пятое, начиная с 5² = 25). И т. д.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Необходимо провести зачёркивание кратных для всех простых чисел p, для которых p² ≤ n. В результате все составные числа будут зачеркнуты, а незачеркнутыми останутся все простые числа.

Для n = 30 уже после зачёркивания кратных числу 5 все составные числа получаются зачеркнутыми:

2 3 5 7 11 13 17 19 23 29