Лабораторная работа №3 Определение вязкости жидкости методом Стокса

1. Литература

1. Трофимова Т.И. Курс физики – М: Издательский центр «Академия», 2005 г. – 560 с. Гл. 1-4

2. Дмитриева В.Ф. Физика: Учеб. пособие – М.: Высшая школа, 2001. – 415 с.

3. Трофимова Т.И. Курс физики: Учебник для студентов вузов.- Высшая школа, 1985, § 177, 178, 181.

4. Трофимова Т.И. Сборник задач по курсу физики для втузов. – М.: «Оникс 21 век», 2005. – 385 с.

5. Трофимова Т.И. Сборник задач по курсу физики с решениями: Учеб. пособие для вузов. – М.: Высшая школа, 2006. – 591 с.

2. Цель работы

Опытное определение динамической вязкости жидкости при данной температуре методом Стокса (падающего шарика).

3. Оборудование

1. Сосуд с жидкостью. 2. Шарики. 3. Микрометр. 4 Масштабная линейка. 5. Секундомер.

4. Основные теоретические сведения

При движении жидкости между ее слоями возникают силы внутреннего трения, действующие таким образом, чтобы уровнять скорости всех слоев. Возникновение этих сил объясняется тем, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество движения, вследствие чего последний начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения, что приводит к его торможению.

Рассмотрим жидкость, движущуюся в направлении оси Х (рис.3.1.).

П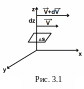 усть слои движутся с разными скоростями. На оси Z возьмем две точки, находящиеся на расстоянии dz. Скорости потока отличаются в этих точках на величину dV. Отношение характеризует изменение скорости потока в направлении оси Z и называется градиентом скорости.

Сила внутреннего трения (вязкости) f, действующая между двумя слоями пропорциональна площади их соприкосновения и градиенту скорости ;

(1)

Величина  - называется динамической вязкостью. Если в формуле (1) положить числено =1 и , то получим =ƒ, т.е. динамическая вязкость численно равна силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого при градиенте скорости, равном единице.

Размерность динамической вязкости , как следует из уравнения (1), выражается в единицах СИ, в кг/(м с), Πа*с.

Динамическая вязкость зависит от природы жидкости и для данной жидкости с повышением температуры уменьшается. Вязкость играет существенную роль при движении жидкостей. Слой жидкости, непосредственно прилегающий к твердой поверхности, в результате прилипания остается неподвижным относительно ее. Скорость остальных слоев возрастает по мере удаления от твердой поверхности. Наличие слоя жидкости между трущимися поверхностями твердых тел способствует уменьшению коэффициента трения.

Опыты показывают, что силы внутреннего трения зависят от скорости движения тела, от геометрической формы тела, его линейных размеров, состояния поверхности тела и вязкости среды.

Силу внутреннего трения ƒ можно наиболее просто определить для тела сферической формы (шарика), движущегося в покоящейся жидкости. Теоретические расчеты, выполненные Дж.Стоксом, приводят к выражению:

(2)

где  - динамическая вязкость;

d – диаметр шарика;

V – скорость шарика.

Если шарик свободно падает в вязкой жидкости (рис.3.2.), то на него, кроме силы внутреннего трения f будут действовать сила тяжести и выталкивающая сила, равная весу жидкости в объеме шарика (V – объем шарика, - плотность жидкости, m – масса шарика,  - плотность шарика).

Результирующая двух сил Fтяж и - равна:

(3)

Рис. 3.2.

Под влиянием сил f и F шарик движется с ускорением а основной закон динамики (второй закон Ньютона) для рассматриваемого случая запишется так:

(4)

где m – масса шарика.

Сила F увеличивает скорость шарика. Наряду с возрастанием скорости шарика увеличивается и сила внутреннего трения f среды, в которой перемещается шарик. По мере падения шарика наступит момент, когда абсолютные значения F и f будут одинаковы, а ускорение равно нулю.

Дальнейшее движение шарика происходит равномерно со скоростью V. Тогда:

(5)

Подставляя значение объема шарика и решая относительно , получим

(6)

Скорость равномерного движения V можно определить по наблюдению времени t прохождения шарика определенного пути l тогда формула (6) принимает вид

(7)

Таким образом, наблюдая за равномерным движением шарика в жидкости, можно определить динамическую вязкость, что и является задачей данной работы.

Следует иметь в виду, что динамическая вязкость сильно зависит от температуры и с ее возрастанием уменьшается.