6. Порядок выполнения работы

1. На технических весах определить массу m (кг) груза Q с точностью кг

2. Штангенциркулем определить диаметр D (м) шкива

3. Вращением маховика поднять груз Q на высоту h (м) от пола, измерить масштабной линейкой высоту h, м

4. Определить время опускания груза Q до пола. Для этого отпустить маховик и включить секундомер, в момент удара груза о пол секундомер выключить.

5. Опыт повторить 5 раз, результат занести в таблицу

Таблица 1.1.

NN/ nn	, м
	t, c
1
2
3
4
5
Среднее значение	<t>	<Δt>

6. Определить среднее значение времени падения груза

7. Обработка результатов измерений

1. Вычислить погрешность измерения времени (i- номер измерения), определить среднюю абсолютную погрешность

2. По расчетной формуле (9) вычислить момент инерции маховика J(кг* )

3. Вычислить относительную погрешность 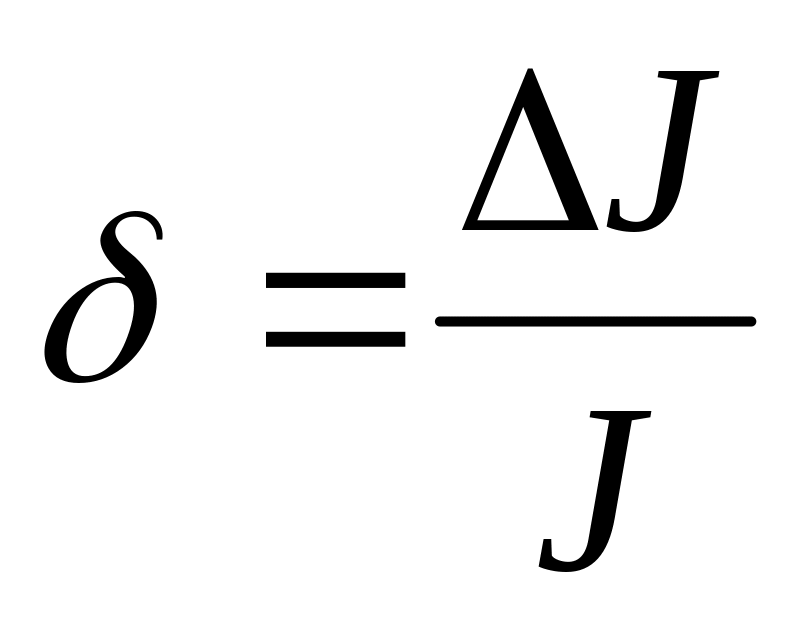по формуле

4. Рассчитать абсолютную погрешность

5. Опытное значение момента инерции записать в виде кг* )

8. Контрольные вопросы

1. Какое движение называется вращательным?

2. Физический смысл угловой скорости и углового ускорения .

3. Что называется моментом инерции J?

4. Запишите основное уравнение динамики вращательного движения.

5. Как вычислить кинетическую энергию вращательного движения.

6. Сформулируйте закон сохранения момента количества движения (момента импульса).

9. Задачи для СРС [2], гл. 1-4, стр. 45

Лабораторная работа №2 проверка законов математического маятника и Определение ускорения силы тяжести при помощи математического маятника

1. Литература

1. Трофимова Т.И. Курс физики – М: Издательский центр «Академия», 2005 г. – 560 с. Гл. 1-4

2. Дмитриева В.Ф. Физика: Учеб. пособие – М.: Высшая школа, 2001. – 415 с.

3. Трофимова Т.И. Курс физики: Учебник для студентов вузов.- Высшая школа, 1985, § 177, 178, 181.

4. Трофимова Т.И. Сборник задач по курсу физики для втузов. – М.: «Оникс 21 век», 2005. – 385 с.

5. Трофимова Т.И. Сборник задач по курсу физики с решениями: Учеб. пособие для вузов. – М.: Высшая школа, 2006. – 591 с.

2. Цель работы

Опытное определение силы тяжести при помощи математического маятника в условиях данной местности.

3. Оборудование

1. Металлический шарик, подвешенный на нити. 2. Линейка. 3. Секундомер.

4. Основные теоретические сведения

Колебаниями называются движения или процессы, которые характеризуются определённой повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например, качание маятника часов, переменный электрический ток и т.д.

При колебательном движении маятника периодически через равные промежутки времени изменяется координата его центра масс, в случае переменного тока периодически изменяются напряжение и сила тока в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Рассмотрение гармонических колебаний важно по двум причинам:

1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;

2) различные периодические процессы можно представить, как наложение гармонических колебаний

Гармонические колебания описываются уравнением:

(1)

где А – максимальное значение колеблющейся величины, называемой амплитудой колебаний.

ω – круговая (циклическая) частота,

φ₀ – начальная фаза колебаний в момент времени t=0,

(ωt+φ₀) – фаза колебаний в момент времени t.

Так как синус изменяется в пределах от +1 до -1, то Х может принимать значения от +А до - А.

Определённые состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебаний получает приращение 2π.

(2)

Величина обратная периоду колебаний:

(3)

т.е. равная числу колебаний, совершаемых в единицу времени, называется линейной частотой колебаний.

Решая (2) и (3) получим:

Единица частоты – герц (Гц): 1 Гц – частота периодического процесса, при которой за 1 сек. совершается одно колебание.

Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координат х от времени t задаётся (1).

Запишем первую и вторую производные по времени от гармонически колеблющейся величины х (скорость υ и ускорение a соответственно):

(4)

(5)

Сила , действующая на колеблющуюся материальную точку, массой m, с учётом (1) и (5) равна:

(6)

Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону.

Примером гармонического колебательного движения является движение математического маятника – идеализированной системы, состоящей из материальной точки массой m, подвешенной на нерастяжимой нити, и колеблющейся под действием силы тяжести. Хорошим приближение математического маятника является небольшой тяжёлый шарик, подвешенный на тонкой нити.

В положении равновесия две силы, действующие на материальную точку: сила тяжести F_тяж = mg и сила натяжения нити F_Н1 уравновешивают друг друга и маятник остаётся в покое.

Рис. 2.1.

Если маятник отклонить от положения равновесия на некоторый угол α, то составляющая силы тяжести, направленная вдоль нити F, уравновесится натяжением нити F_Н2 = mg cos α, а другая составляющая F₁ = -mg sin α , перпендикулярная нити, стремится вернуть маятник в положение равновесия. Эта сила называется возвращающей силой

По второму закону Ньютона колебание маятника описывается уравнением:

(7)

где k = mω². Возвращающей силой является F₁= -mg sin α.

При малых углах sin α ≈ α, , , значит

или , а т.к. , то

(8)