Т p еорема 3

П

F1

F2

УСТЬ НА ОСИ ПЛОСКОСТИ ЗАДАНЫ ФОКУСЫ ЭЛЛИПСА И . СУММА РАССТОЯНИЙ ОТ ПРОИЗВОЛЬНОЙ ТОЧКИ ЭЛЛИПСА ДО ФОКУСОВ РАВНА 2а. (а 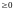). ТОГДА «КАНОНИЧЕСКОЕ» УРАВНЕНИЕ ЭЛЛИПСА ИМЕЕТ ВИД

РИС.6

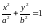, (14)

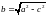ГДЕ (15)

ЗАМЕЧАНИЕ. ФОКУСЫ ЭЛЛИПСА ЛЕЖАТ НА ОСИ ТОГДА И ТОЛЬКО ТОГДА, КОГДА В УРАВНЕНИИ (1.14) .

ОПРЕДЕЛЕНИЕ 6. ЭКСЦЕНТРИСИТЕТОМ ЭЛЛИПСА НАЗЫВАЕТСЯ ВЕЛИЧИНА , КОТОРАЯ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ

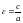(16)

ТАК КАК У ЭЛЛИПСА 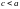, ТО ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ВСЕГДА МЕНЬШЕ ЕДИНИЦЫ. ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ПОКАЗЫВАЕТ, НАСКОЛЬКО СИЛЬНО СПЛЮЩЕН ЭЛЛИПС К ПРЯМОЙ НА КОТОРОЙ ЛЕЖАТ ФОКУСЫ.

УПРАЖНЕНИЕ. ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ. ЧЕМ МЕНЬШЕ ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА, ТЕМ ЭЛЛИПС

1) Более сплющен 2) менее сплющен

ДИРЕКТРИСЫ ЭЛЛИПСА, ФОКУСЫ КОТОРОГО ЛЕЖАТ НА ОСИ , ЗАДАЮТСЯ УРАВНЕНИЯМИ ВЕРТИКАЛЬНЫХ ПРЯМЫХ ЛИНИЙ

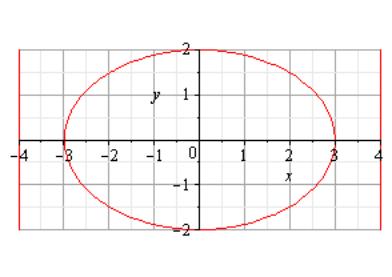
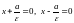(17)

M

D

F

ОТНОШЕНИЕ РАССТОЯНИЙ ОТ ЛЮБОЙ ТОЧКИ ЭЛЛИПСА ДО ФОКУСА И ДО БЛИЖАЙШЕЙ К НЕМУ ДИРЕКТРИСЫ РАВНО ЧИСЛЕННОМУ ЗНАЧЕНИЮ ЭКСЦЕНТРИСИТЕТА (РИС.7)

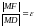(18)

РИС.7

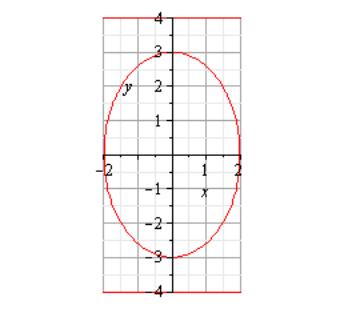
Теорема 4

ЕСЛИ ФОКУСЫ ЭЛЛИПСА 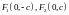РАСПОЛОЖИТЬ НА ОСИ ОУ, ТО ЭЛЛИПС БУДЕТ ИМЕТЬ «КАНОНИЧЕСКОЕ» УРАВНЕНИЕ

, ГДЕ 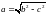(19)

В ФОРМУЛЕ (19) , .

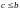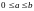РИС. 8

ЗАМЕЧАНИЕ. ФОКУСЫ ЭЛЛИПСА ЛЕЖАТ НА ОСИ ТОГДА И ТОЛЬКО ТОГДА, КОГДА .

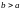АНАЛОГИЧНО ПРЕДЫДУЩЕМУ ОПРЕДЕЛЯЮТСЯ

ЭКСЦЕНТРИСИТЕТ 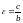(20) ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ПОКАЗЫВАЕТ, НАСКОЛЬКО СИЛЬНО СПЛЮЩЕН ЭЛЛИПС К ПРЯМОЙ НА КОТОРОЙ ЛЕЖАТ ФОКУСЫ.

ДИРЕКТРИСЫ ЭЛЛИПСА,ФОКУСЫ КОТОРОГО ЛЕЖАТ НА ОСИ , ЗАДАЮТСЯ УРАВНЕНИЯМИ ГОРИЗОНТАЛЬНЫХ ПРЯМЫХ ЛИНИЙ

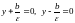(21)

П

РИМЕР 9. НА РИС.9 ПРИВЕДЁН ЧЕРТЁЖ ЭЛЛИПСА И ВЫПИСАНЫ ЕГО УРАВНЕНИЯ В СТАРОЙ И НОВОЙ СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

3

1

РИС.16

РИС.9.

В СТАРОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД

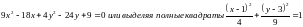
В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД

(СМ. ФОРМУЛУ (1.19))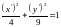 . ЛИНИЯ ЭЛЛИПС.