
Лекция 3. Прямая линия на плоскости. Кривые второго порядка.
Одной из важных задач в математике является задача определения положения точки. Эта задача решается разными способами. Один способ хорошо известен из школьной программы. Это определение положения точки с помощью декартовой системы координат.
Д
 ля
этого на плоскости фиксируются две
взаимно перпендикулярные числовые
оси. Горизонтальная ось
ля
этого на плоскости фиксируются две
взаимно перпендикулярные числовые
оси. Горизонтальная ось
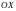 -ось
абсцисс и вертикальная ось
-ось
абсцисс и вертикальная ось
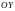 -ось
ординат. Точка пересечения О этих осей
называется началом координат. Плоскость,
на которой введена система координат,
называется координатной плоскостью.
-ось
ординат. Точка пересечения О этих осей
называется началом координат. Плоскость,
на которой введена система координат,
называется координатной плоскостью.

M

Х1
У1
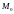
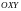 возьмем
произвольную точку
и
проведём через неё прямые параллельные
координатным осям. Пересечение прямой
с осью
даёт
нам единственное число
возьмем
произвольную точку
и
проведём через неё прямые параллельные
координатным осям. Пересечение прямой
с осью
даёт
нам единственное число
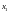 ,
а пересечение прямой с осью
даёт
нам единственное число
,
а пересечение прямой с осью
даёт
нам единственное число .
.
Обратно, если задана
пара чисел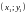 ,
,
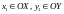 ,то
из рис.1 видно, что она определяет
единственную точку
.
,то
из рис.1 видно, что она определяет
единственную точку
.
рис.1 
Определение 1.
Упорядоченная пара чисел
,
определяющая положение точки
на координатной плоскости называется
прямоугольными декартовыми координатами
точки. Число
называют
абсциссой точки, а число
ординатой
точки
.
Произвольную точку на координатной
плоскости будем обозначать так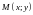 .
Каждая точка
.
Каждая точка
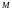 имеет
свои координаты и наоборот каждая пара
координат
имеет
свои координаты и наоборот каждая пара
координат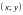 задаёт
одну определённую точку. Каждое правило
теперь может быть сформулировано на
двух разных языках: 1) на геометрическом
языке и 2)на аналитическом языке (языке
координат)
задаёт
одну определённую точку. Каждое правило
теперь может быть сформулировано на
двух разных языках: 1) на геометрическом
языке и 2)на аналитическом языке (языке
координат)
Например, задать точку
на координатной плоскости это значит:
1) либо обозначить её на плоскости, 2)
либо задать её координаты. Найти точку
это значит: 1) либо найти её положение
на координатной плоскости, 2) либо найти
её координаты. Если задавать абсциссу
 и
ординату
и
ординату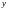 точки
независимо
друг от друга, то на координатной
плоскости получим совершенно произвольные
расположения точек
.
Если же координаты
и
связаны
между собой определённым правилом, то
меняя их по этому правилу, получаем
на плоскости кривую, состоящую из этих
точек.
точки
независимо
друг от друга, то на координатной
плоскости получим совершенно произвольные
расположения точек
.
Если же координаты
и
связаны
между собой определённым правилом, то
меняя их по этому правилу, получаем
на плоскости кривую, состоящую из этих
точек.
Например, если сумма
квадратов координат равна 1
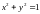 ,
то получаем уравнение окружности
радиуса 1. На практике различные расчёты
с геометрическими объектами производятся
в координатах. Затем, если это нужно,
полученные результаты переводятся
для наглядности на геометрический язык.
На языке координат задать линию значит
задать правило связывающее между собой
ординату
и
абсциссу
.
Такое правило называется уравнением
линии в координатной плоскости.
,
то получаем уравнение окружности
радиуса 1. На практике различные расчёты
с геометрическими объектами производятся
в координатах. Затем, если это нужно,
полученные результаты переводятся
для наглядности на геометрический язык.
На языке координат задать линию значит
задать правило связывающее между собой
ординату
и
абсциссу
.
Такое правило называется уравнением
линии в координатной плоскости.
Простейшие преобразования декартовой системы координат. Параллельныйсдвиг осей координат.
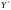
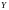
П

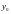

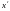
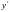
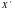
 ИМЕЕТ
КООРДИНАТЫ
ИМЕЕТ
КООРДИНАТЫ .
ПОМЕСТИМ НАЧАЛО НОВОЙ СИСТЕМЫ КООРДИНАТ
.
ПОМЕСТИМ НАЧАЛО НОВОЙ СИСТЕМЫ КООРДИНАТ
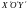 В
ТОЧКУ
.
ОСЬ
В
ТОЧКУ
.
ОСЬ
 НАПРАВИМ
ПАРАЛЛЕЛЬНО ОСИ
,
А ОСЬ
НАПРАВИМ
ПАРАЛЛЕЛЬНО ОСИ
,
А ОСЬ
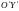 ПАРАЛЛЕЛЬНО
ОСИ
.
ТОГДА В НОВОЙ СИСТЕМЕ КООРДИНАТ
ТОЧКА
БУДЕТ
ИМЕТЬ КООРДИНАТЫ
ПАРАЛЛЕЛЬНО
ОСИ
.
ТОГДА В НОВОЙ СИСТЕМЕ КООРДИНАТ
ТОЧКА
БУДЕТ
ИМЕТЬ КООРДИНАТЫ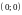 (РИС.13)
. ЕСЛИ ТЕПЕРЬ НА ПЛОСКОСТИ РАССМОТРИМ
ПРОИЗВОЛЬНУЮ ТОЧКУ
,
ИМЕЮЩУЮ В СТАРОЙ СИСТЕМЕ КООРДИНАТ
КООРДИНАТЫ
,
ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ
ИМЕТЬ КООРДИНАТЫ
(РИС.13)
. ЕСЛИ ТЕПЕРЬ НА ПЛОСКОСТИ РАССМОТРИМ
ПРОИЗВОЛЬНУЮ ТОЧКУ
,
ИМЕЮЩУЮ В СТАРОЙ СИСТЕМЕ КООРДИНАТ
КООРДИНАТЫ
,
ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ
ИМЕТЬ КООРДИНАТЫ
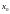
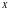
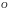
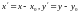 (1)
(1)
ПЕРЕХОД ОТ КООРДИНАТНОЙ СИСТЕМЫ К СИСТЕМЕ НАЗОВЕМ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ КООРДИНАТ (РИС.).
Найдем уравнение простейшей линии, которая, тем не менее, играет одну из важных ролей в математике.
Вывод уравнения прямой линии и исследование прямой линии на координатной плоскости.
О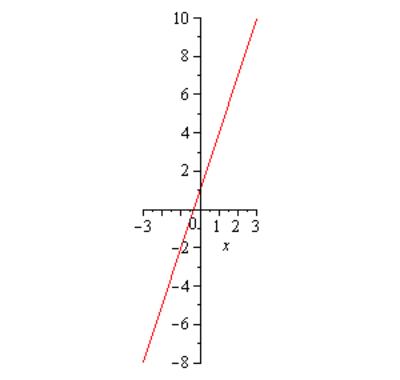

Р
ПРЕДЕЛЕНИЕ 2. УГОЛ НАКЛОНА ПРЯМОЙ К ОСИ ОХ ИЗМЕРЯЕТСЯ ПОВОРОТОМ (вокруг точки Р) ПРОТИВ ЧАСОВОЙ СТРЕЛКИ ОСИ ОХ ДО СОВПАДЕНИЯ С ПРЯМОЙ. РИС.2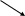
РИС.2
ПРАВИЛО 1. ЕСЛИ ЧЕРЕЗ ЗАДАННЫЕ ТОЧКИ НА ПРЯМОЙ ПРОВЕСТИ ГОРИЗОНТАЛЬНЫЕ ПРЯМЫЕ, ТО ВСЕ ПОЛУЧЕННЫЕ УГЛЫ БУДУТ РАВНЫ ( КАК УГЛЫ С ВЗАИМНО ПАРАЛЛЕЛЬНЫМИ СТОРОНАМИ) УГЛУ НАКЛОНА ПРЯМОЙ К ОСИ ОХ. РИС.3.
РИС.3
K
M
M


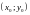 И
ПЕРЕМЕННУЮ ТОЧКУ
С КООРДИНАТАМИ
.
ПРОВЕДЁМ ЧЕРЕЗ ТОЧКУ
ГОРИЗОНТАЛЬНУЮ
ПРЯМУЮ, А ЧЕРЕЗ ТОЧКУ
ВЕРТИКАЛЬНУЮ
ПРЯМУЮ. ТРЕУГОЛЬНИК
И
ПЕРЕМЕННУЮ ТОЧКУ
С КООРДИНАТАМИ
.
ПРОВЕДЁМ ЧЕРЕЗ ТОЧКУ
ГОРИЗОНТАЛЬНУЮ
ПРЯМУЮ, А ЧЕРЕЗ ТОЧКУ
ВЕРТИКАЛЬНУЮ
ПРЯМУЮ. ТРЕУГОЛЬНИК
 ПРЯМОУГОЛЬНЫЙ.
ОТНОШЕНИЕ
ПРЯМОУГОЛЬНЫЙ.
ОТНОШЕНИЕ
 ЧИСЛЕННО
РАВНО ТАНГЕНСУ УГЛА
(РИС.4).
ПЕРЕХОДЯ К КООРДИНАТАМ ПОЛУЧАЕМ
ЧИСЛЕННО
РАВНО ТАНГЕНСУ УГЛА
(РИС.4).
ПЕРЕХОДЯ К КООРДИНАТАМ ПОЛУЧАЕМ

 =
=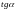 .
ТАК КАК СОГЛАСНО
ПРАВИЛУ 1.1 УГОЛ
РАВЕН УГЛУ НАКЛОНА
ПРЯМОЙ К ОСИ ОХ, ТО КАКУЮ БЫ
ТОЧКУ
НА
ПРЯМОЙ НИ ВЗЯТЬ ВЕЛИЧИНА
БУДЕТ
ДЛЯ ДАННОЙ ПРЯМОЙ ПОСТОЯННОЙ. ЭТУ
ВЕЛИЧИНУ НАЗЫВАЮТ УГЛОВЫМ КОЭФФИЦИЕНТОМ
ДАННОЙ ПРЯМОЙ И ОБЫЧНО ОБОЗНАЧАЮТ
БУКВОЙ
.
ТАК КАК СОГЛАСНО
ПРАВИЛУ 1.1 УГОЛ
РАВЕН УГЛУ НАКЛОНА
ПРЯМОЙ К ОСИ ОХ, ТО КАКУЮ БЫ
ТОЧКУ
НА
ПРЯМОЙ НИ ВЗЯТЬ ВЕЛИЧИНА
БУДЕТ
ДЛЯ ДАННОЙ ПРЯМОЙ ПОСТОЯННОЙ. ЭТУ
ВЕЛИЧИНУ НАЗЫВАЮТ УГЛОВЫМ КОЭФФИЦИЕНТОМ
ДАННОЙ ПРЯМОЙ И ОБЫЧНО ОБОЗНАЧАЮТ
БУКВОЙ
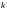
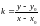 (2)
(2)
или
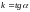 (3)
(3)
рис.4.
ПРИМЕР
1 НАЙТИ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ ПРЯМЫХ ЛИНИЙ,
ПРОХОДЯЩИХ ЧЕРЕЗ ТОЧКИ 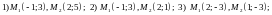
РЕШЕНИЕ.
1) ВЫЧИСЛЯЕМ ПРИРАЩЕНИЯ ОРДИНАТЫ
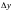 И
АБСЦИССЫ
И
АБСЦИССЫ
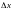
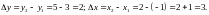 ПО
ФОРМУЛЕ (1)
ОПРЕДЕЛЯЕМ УГЛОВОЙ КОЭФФИЦИЕНТ НАКЛОНА
ПРЯМОЙ а)
ПО
ФОРМУЛЕ (1)
ОПРЕДЕЛЯЕМ УГЛОВОЙ КОЭФФИЦИЕНТ НАКЛОНА
ПРЯМОЙ а)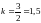 .
2) АНАЛОГИЧНО
ОПРЕДЕЛЯЕМ УГЛОВОЙ КОЭФФИЦИЕНТ ВТОРОЙ
ПРЯМОЙ
.
2) АНАЛОГИЧНО
ОПРЕДЕЛЯЕМ УГЛОВОЙ КОЭФФИЦИЕНТ ВТОРОЙ
ПРЯМОЙ
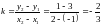 .
3) УГЛОВОЙ КОЭФФИЦИЕНТ ТРЕТЬЕЙ ПРЯМОЙ
.
3) УГЛОВОЙ КОЭФФИЦИЕНТ ТРЕТЬЕЙ ПРЯМОЙ
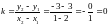 .
.
ДАННЫЙ ПРИМЕР ПОКАЗЫВАЕТ, ЧТО УГЛОВОЙ КОЭФФИЦИЕНТ МОЖЕТ БЫТЬ ЛИБО ПОЛОЖИТЕЛЬНЫМ, ЛИБО ОТРИЦАТЕЛЬНЫМ, ЛИБО РАВНЫМ НУЛЮ.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ УГЛОВОГО КОЭФФИЦИЕНТА УРАВНЕНИЯ ПРЯМОЙ.
ЕСЛИ
УГЛОВОЙ КОЭФФИЦИЕНТ ,
то угол наклона прямой к оси ОХ тупой
.
,
то угол наклона прямой к оси ОХ тупой
.
ЕСЛИ
УГЛОВОЙ КОЭФФИЦИЕНТ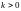 ,
то угол наклона прямой к оси ОХ острый
.
,
то угол наклона прямой к оси ОХ острый
.
ЕСЛИ
УГЛОВОЙ КОЭФФИЦИЕНТ
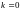 ,
ТО ПРЯМАЯ ЛИНИЯ
ГОРИЗОНТАЛЬНА.
,
ТО ПРЯМАЯ ЛИНИЯ
ГОРИЗОНТАЛЬНА.
ПРАВИЛО 2.
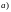 ДВЕ
ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ ТОГДА И ТОЛЬКО
ТОГДА ЕСЛИ ИХ УГЛОВЫЕ КОЭФФИЦИЕНТЫ
РАВНЫ
ДВЕ
ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ ТОГДА И ТОЛЬКО
ТОГДА ЕСЛИ ИХ УГЛОВЫЕ КОЭФФИЦИЕНТЫ
РАВНЫ
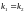 .
.
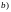 ЕСЛИ
( НЕВЕРТИКАЛЬНАЯ И НЕГОРИЗОНТАЛЬНАЯ)
ПРЯМАЯ ИМЕЕТ УГЛОВОЙ КОЭФФИЦИЕНТ
НАКЛОНА
,
ТО ПЕРПЕНДИКУЛЯРНАЯ К НЕЙ ПРЯМАЯ
ИМЕЕТ УГЛОВОЙ КОЭФФИЦИЕНТ
НАКЛОНА
ЕСЛИ
( НЕВЕРТИКАЛЬНАЯ И НЕГОРИЗОНТАЛЬНАЯ)
ПРЯМАЯ ИМЕЕТ УГЛОВОЙ КОЭФФИЦИЕНТ
НАКЛОНА
,
ТО ПЕРПЕНДИКУЛЯРНАЯ К НЕЙ ПРЯМАЯ
ИМЕЕТ УГЛОВОЙ КОЭФФИЦИЕНТ
НАКЛОНА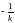 .Доказательство.
ПУНКТ
а) ПРАВИЛА
ОЧЕВИДЕН (СМ.
ПРАВИЛО 1).
.Доказательство.
ПУНКТ
а) ПРАВИЛА
ОЧЕВИДЕН (СМ.
ПРАВИЛО 1).
B
A
C
D
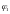
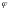
 ).
ПУСТЬ ПРЯМАЯ
).
ПУСТЬ ПРЯМАЯ
 С УГЛОВЫМ КОЭФФИЦИЕНТОМ
перпендикулярна
прямой
С УГЛОВЫМ КОЭФФИЦИЕНТОМ
перпендикулярна
прямой
 С УГЛОВЫМ КОЭФФИЦИЕНТОМ
С УГЛОВЫМ КОЭФФИЦИЕНТОМ
 .
Угловой коэффициент наклона прямой
:
равен
,
а угловой коэффициент наклона
прямой
:
.
Угловой коэффициент наклона прямой
:
равен
,
а угловой коэффициент наклона
прямой
: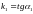 .
В любом треугольнике всякий внешний
угол равен сумме двух внутренних углов
не смежных с ним (РИС.5).
.
В любом треугольнике всякий внешний
угол равен сумме двух внутренних углов
не смежных с ним (РИС.5).
рис.5.
Отсюда
внешний угол
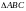 равен
равен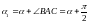 .
Поэтому угловой
коэффициент наклона прямой
равен:
.
Поэтому угловой
коэффициент наклона прямой
равен: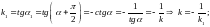 Пункт
правила
2 доказан.
Пункт
правила
2 доказан.
СЛЕДУЮЩЕЕ ПРАВИЛО ПОЗВОЛЯЕТ ВЫЧИСЛЯТЬ УГОЛ МЕЖДУ ПРЯМЫМИ ЛИНИЯМИ.
ПРАВИЛО
3 . ОБОЗНАЧИМ
ОСТРЫЙ
УГОЛ
МЕЖДУ ПРЯМОЙ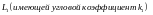
 И
ПРЯМОЙ
И
ПРЯМОЙ
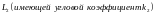 ЧЕРЕЗ
.
ТОГДА СПРАВЕДЛИВА
ФОРМУЛА:
ЧЕРЕЗ
.
ТОГДА СПРАВЕДЛИВА
ФОРМУЛА:
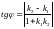 (4)
(4)
Д
A
B
C
D
ОКАЗАТЕЛЬСТВО. В ЛЮБОМ ВСЯКИЙ ВНЕШНИЙ УГОЛ РАВЕН СУММЕ ДВУХ ВНУТРЕННИХ НЕ СМЕЖНЫХ С НИМ. ОБОЗНАЧИМ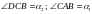 ;
;
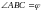 СЛЕДОВАТЕЛЬНО
( СМ. РИС.6)
СЛЕДОВАТЕЛЬНО
( СМ. РИС.6)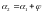 .
ВЫЧИСЛИМ ТАНГЕНС ОТ ОБЕИХ
ЧАСТЕЙ РАВЕНСТВА
.
ВЫЧИСЛИМ ТАНГЕНС ОТ ОБЕИХ
ЧАСТЕЙ РАВЕНСТВА

РИС.6
ЧТОБЫ ВЫЧИСЛИТЬ ОСТРЫЙ УГОЛ НУЖНО ФОРМУЛУ СПРАВА БРАТЬ ПО МОДУЛЮ. ПРАВИЛО 1.3 ДОКАЗАНО.
ПРИМЕР
3 ИСПОЛЬЗУЯ
ПРАВИЛО 1.2 ДОКАЗАТЬ, ЧТО ЧЕТЫРЕХУГОЛЬНИК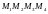
ПАРАЛЛЕЛОГРАММ,
ГДЕ
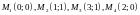 .
.
РЕШЕНИЕ. ПАРАЛЛЕЛОГРАММ ЭТО ЧЕТЫРЁХУГОЛЬНИК, У КОТОРОГО ПРОТИВОПОЛОЖНЫЕ СТОРОНЫ ПАРАЛЛЕЛЬНЫ.
ВЫЧИСЛИМ
НАКЛОНЫ ПРЯМЫХ
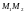 ,
,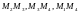
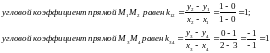
ТАК
КАК
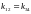 ,
то по правилу 1.2 пункт а) сторона
параллельна стороне
,
то по правилу 1.2 пункт а) сторона
параллельна стороне .
Далее
.
Далее
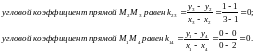
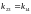 отсюда следует, что сторона
отсюда следует, что сторона
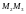 параллельна стороне
параллельна стороне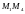 .
Что и требовалось
.
Что и требовалось
доказать.
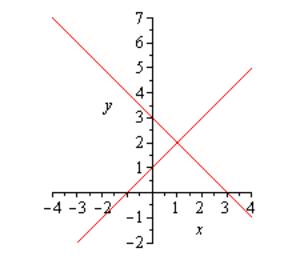
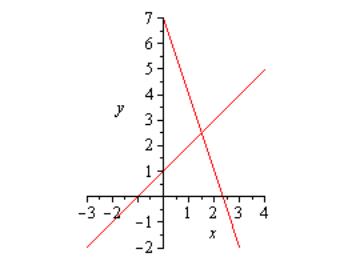
ПРИМЕР
4. ВЫЧИСЛИТЬ
УГОЛ МЕЖДУ ПРЯМЫМИ
ЛИНИЯМИ,
ИМЕЮЩИМИ СООТВЕТСТВУЮЩИЕ УГЛОВЫЕ
КОЭФФИЦИЕНТЫ:
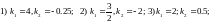
РЕШЕНИЕ.
В ПЕРВОМ ПРИМЕРЕ УГЛОВОЙ КОЭФФИЦИЕНТ
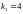 ,
,
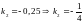 .
ТАК КАК
.
ТАК КАК
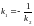 ,
ТО ПО ПРАВИЛУ 2
в) ДАННЫЕ ПРЯМЫЕ
ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ. ВО ВТОРОМ
ПРИМЕРЕ
,
ТО ПО ПРАВИЛУ 2
в) ДАННЫЕ ПРЯМЫЕ
ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ. ВО ВТОРОМ
ПРИМЕРЕ
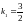 ,
,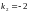 .
Тангенс острого угла вычисляем по
формуле(3)
.
Тангенс острого угла вычисляем по
формуле(3) 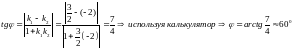
В
ТРЕТЬЕМ ПРИМЕРЕ
 .
.
УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ НА ПЛОСКОСТИ.
У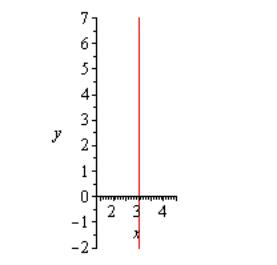 РАВНЕНИЕ
ВЕРТИКАЛЬНОЙ ПРЯМОЙ ЛИНИИ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКУ
РАВНЕНИЕ
ВЕРТИКАЛЬНОЙ ПРЯМОЙ ЛИНИИ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКУ
 ,
ИМЕЕТ ВИД
,
ИМЕЕТ ВИД
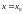 (5)
(5)
ТАК КАК СОСТОИТ ИЗ ТОЧЕК, У КОТОРЫХ АБСЦИССА ПОСТОЯННА И РАВНА (РИС.7) . ТАКАЯ ПРЯМАЯ ПАРАЛЛЕЛЬНА ОСИ ОУ.
РИС.7
УРАВНЕНИЕ НЕВЕРТИКАЛЬНОЙ ПРЯМОЙ ЛИНИИ НА ПЛОСКОСТИ.
ЕСЛИ
НЕВЕРТИКАЛЬНАЯ ПРЯМАЯ ЛИНИЯ ПРОХОДИТ
ЧЕРЕЗ ДВЕ ТОЧКИ
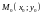 И
.
ТОГДА УГЛОВОЙ КОЭФФИЦИЕНТ ПРЯМОЙ РАВЕН
И
.
ТОГДА УГЛОВОЙ КОЭФФИЦИЕНТ ПРЯМОЙ РАВЕН
ДЛЯ ЛЮБОЙ ТОЧКИ ЛЕЖАЩЕЙ НА ДАННОЙ ПРЯМОЙ.
УМНОЖАЯ
ОБЕ ЧАСТИ РАВЕНСТВА
НА МНОЖИТЕЛЬ (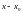 ),
ПОЛУЧАЕМ УРАВНЕНИЕ ПРЯМОЙ
),
ПОЛУЧАЕМ УРАВНЕНИЕ ПРЯМОЙ
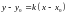 (6)
(6)
УРАВНЕНИЕ (6) НАЗЫВАЕТСЯ УРАВНЕНИЕМ ПРЯМОЙ ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКУ С УГЛОВЫМ КОЭФФИЦИЕНТОМ .
ЗАМЕЧАНИЕ. УРАВНЕНИЕ ПРЯМОЙ (6) ПОКАЗЫВАЕТ НАМ, ЧТО ПРЯМАЯ ЛИНИЯ ПРОХОДИТ ЧЕРЕЗ ТОЧКУ и ЧТО ТАНГЕНС УГЛА НАКЛОНА ПРЯМОЙ К ОСИ ОХ ЧИСЛЕННО РАВЕН УГЛОВОМУ КОЭФФИЦИЕНТУ .
У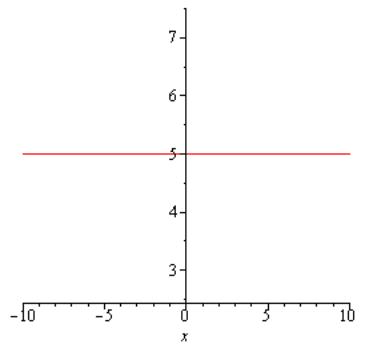 РАВНЕНИЕ
ГОРИЗОНТАЛЬНОЙ ПРЯМОЙ
РАВНЕНИЕ
ГОРИЗОНТАЛЬНОЙ ПРЯМОЙ
ЕСЛИ
УГОЛ НАКЛОНА ПРЯМОЙ РАВЕН

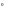 И ПОЭТОМУ
И ПОЭТОМУ
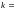 0, ТО ИЗ УРАВНЕНИЯ ПРЯМОЙ (1.6)
ПОЛУЧАЕМ УРАВНЕНИЕ
0, ТО ИЗ УРАВНЕНИЯ ПРЯМОЙ (1.6)
ПОЛУЧАЕМ УРАВНЕНИЕ
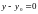 (7)
(7)
ПРЯМАЯ СОСТОИТ ИЗ ТОЧЕК, У КОТОРЫХ ОРДИНАТА ПОСТОЯННА И РАВНА . ТАКАЯ ПРЯМАЯ ПАРАЛЛЕЛЬНА ОСИ ОХ ( РИС. 8).
РИС.8
СПЕЦИАЛЬНЫЕ СЛУЧАИ ЗАДАНИЯ УРАВНЕНИЙ ПРЯМОЙ ЛИНИИ.
УРАВНЕНИЕ ПРЯМОЙ ЛИНИИ В ОТРЕЗКАХ.
ЕСЛИ
ПРЯМАЯ ЛИНИЯ ПРОХОДИТ ЧЕРЕЗ ТОЧКИ
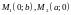 ,
ЛЕЖАЩИЕ НА ОСЯХ ОУ И ОХ
,
ЛЕЖАЩИЕ НА ОСЯХ ОУ И ОХ
СООТВЕТСТВЕННО, ТО УРАВНЕНИЕ (6) МОЖНО ПРЕОБРАЗОВАТЬ К ВИДУ
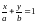 (8)
(8)
УРАВНЕНИЕ
ТАКОГО ВИДА НАЗЫВАЮТ УРАВНЕНИЕМ
ПРЯМОЙ В ОТРЕЗКАХ,
ТАК КАК ПРЯМАЯ ЛИНИЯ ОТСЕКАЕТ НА ОСЯХ
ОХ И ОУ ОТРЕЗКИ ДЛИНОЙ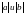 СООТВЕТСТВЕННО.
СООТВЕТСТВЕННО.
ВСЕ РАССМОТРЕННЫЕ УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ МОЖНО ПРЕОБРАЗОВАТЬ В УРАВНЕНИЕ
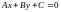 (9)
(9)
ПОЭТОМУ ЭТО УРАВНЕННИЕ НАЗЫВАЮТ ОБЩИМ УРАВНЕНИЕМ ПРЯМОЙ.
ПРИМЕР
5. ЗАПИСАТЬ
УРАВНЕНИЕ ПРЯМОЙ
ЛИНИИ
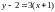 В ВИДЕ : 1)
ОБЩЕГО УРАВНЕНИЯ,
В ВИДЕ : 1)
ОБЩЕГО УРАВНЕНИЯ,
