Розділ 2. Статистичні оцінки параметрів розподілу Точкові оцінки

Точковою називають статистичну оцінку, яка визначається одним числом.

Незміщеною називають точкову оцінку, математичне сподівання якої дорівнює оцінюваному параметру при будь-якому обсягу вибірки.

Зміщеною називають точкову оцінку, математичне сподівання якої не дорівнює оцінюваному параметру.

Незміщеною оцінкою генеральної середньої (математичного сподівання) служить вибіркова середня

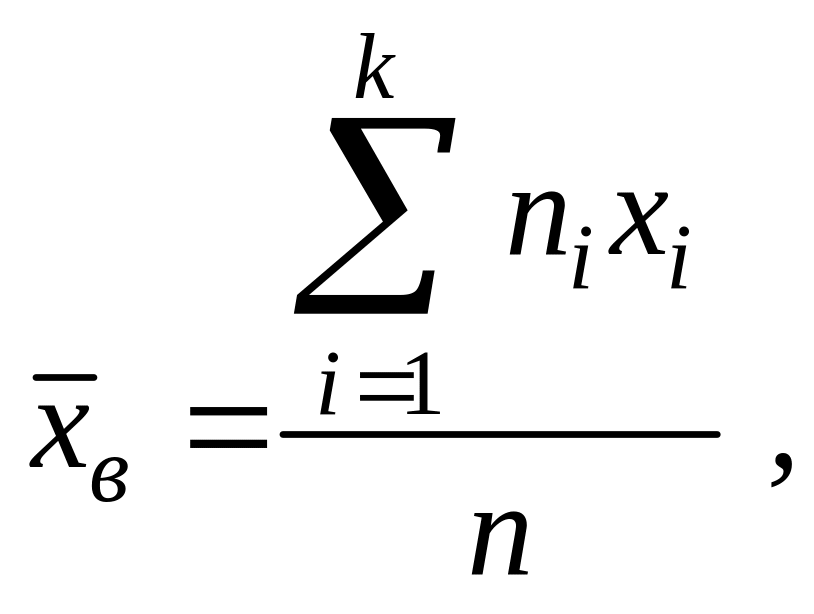
де – варіанта вибірки, – частота варіанти , – обсяг вибірки.

Зміщеною оцінкою генеральної дисперсії служить вибіркова середня

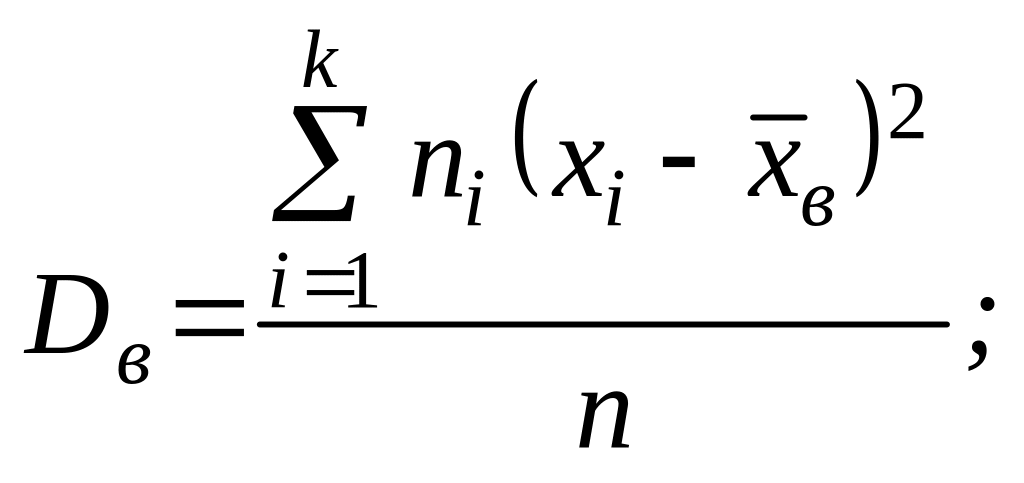
ця оцінка є зміщеною, так як

Більш зручна формула

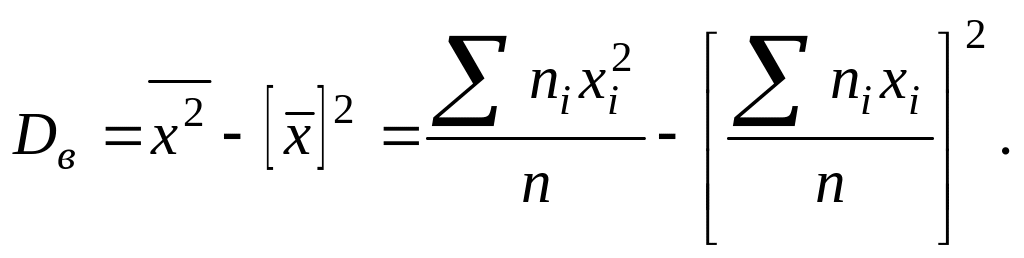
Незміщеною оцінкою генеральної дисперсії служить виправлена вибіркова дисперсія

Більш зручна формула

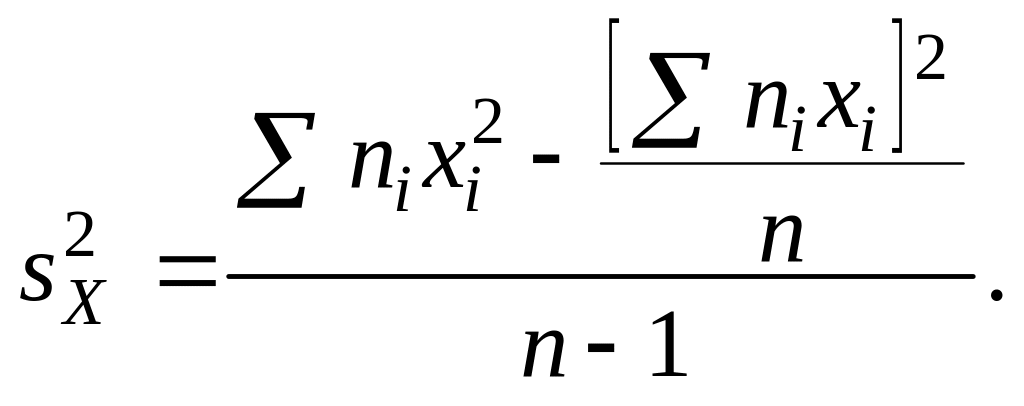
В умовних варіантах вона має вигляд

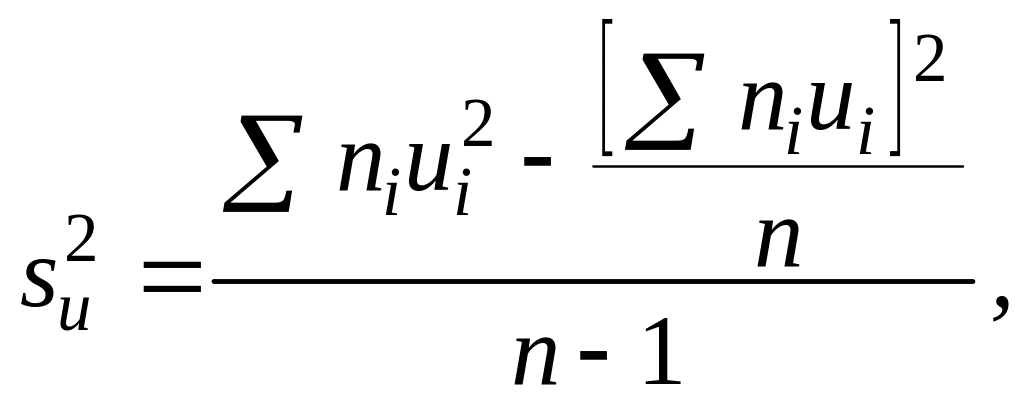
причому, якщо , то ; якщо , то .

Інтервальні оцінки

Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервалу, що покриває оцінюваний параметр.

Довірчим називають інтервал, який із заданою надійністю покриває оцінюваний параметр.

Для оцінки математичного сподівання нормально розподіленої кількісної ознаки по вибірковій середній з а в і д о м и м с е р е д н і м к в а д р а т и ч н и м в і д х и л е н н я м генеральної сукупності служить довірчий інтервал

де – точність оцінки; – обсяг вибірки; є таке значення аргументу функції Лапласа , за яким ; з а н е в і д о м и м (і обсязі вибірки )

де – виправлене середнє квадратичне відхилення, знаходять за таблицею за заданими і .

Для оцінки середнього квадратичного відхилення нормально розподіленої кількісної ознаки з надійністю за виправленим вибірковим середнім квадратичним відхиленням служать довірчі інтервали

де знаходять за таблицею за заданими і .

Методи розрахунку зведених характеристик вибірки Метод добутків обчислення вибіркових середньої та дисперсії Рівновіддалені варіанти

Нехай вибірка задана у вигляді розподілу рівновіддалених варіант і відповідних їм частот. У цьому випадку зручно знаходити вибіркові середню та дисперсію методом добутків за формулами

де – крок (різниця між двома сусідніми варіантами); – хибний нуль (варіанта, яка має найбільшу частоту);

– умовна варіанта;

– умовний момент першого порядку;

– умовний момент другого порядку.

Асиметрія та ексцес емпіричного розподілу

Асиметрія та ексцес емпіричного розподілу визначається відповідно рівностями:

тут – вибіркове середнє квадратичне відхилення; та – центральні емпіричні моменти третього та четвертого порядків:

Ці моменти у випадку рівновіддалених варіант з кроком (крок дорівнює різниці між будь-якими двома сусідніми варіантами) зручно обчислювати за формулами:

де – умовні моменти порядку; – умовні варіанти. Тут – початкові варіанти, – хибний нуль, тобто варіанта, яка має найбільшу частоту (або будь-яка варіанта, розташована приблизно в середині варіаційного ряду).

Отже, для відшукання асиметрії та ексцесу необхідно обчислити умовні моменти, що можна зробити методом добутків або методом сум.