Частина 2. Математична статистика

1. Знайти методом добутків:

а) вибіркову середню;

б) вибіркову дисперсію;

в) вибіркове середнє квадратичне відхилення за даним статистичним розподілом.

1. 	105	110	115	120	125	130	135
   	4	6	10	40	20	12	8

2. 	12,5	13,0	13,5	14,0	14,5	15,0	15,5
   	5	15	40	25	8	4	3

3. 	10,2	10,9	11,6	12,3	13,0	13,7	14,4
   	8	10	60	12	5	3	2

4. 	45	50	55	60	65	70	75
   	4	6	10	40	20	12	8

5. 	110	115	120	125	130	135	140
   	5	10	30	25	15	10	5

6. 	12,4	16,4	20,4	24,4	28,4	32,4	36,4
   	5	15	40	25	8	4	3

7. 	26	32	38	44	50	56	62
   	5	15	40	23	8	4	3

	10,6	15,6	20,6	25,6	30,6	35,6	40,6
	8	10	60	12	5	3	2

9. 	100	110	120	130	140	150	160
   	4	6	10	40	20	12	8

10. 	130	140	150	160	170	180	190
    	5	10	30	25	15	10	5

11. 	13	14	15	16	17	18	19
    	2	8	12	30	20	18	10

12. 	10	12	14	16	18	20	22
    	3	9	15	41	27	10	5

13. 	11	13	15	17	19	21	23
    	4	7	12	20	13	8	6

	10,5	11,0	11,5	12,0	12,5	13,0	13,5
	4	6	10	40	20	12	8

15. 	125	130	135	140	145	150	155
    	5	15	40	25	8	4	3

16. 	102	109	116	123	130	137	144
    	8	10	60	12	5	3	2

17. 	4,5	5,0	5,5	6,0	6,5	7,0	7,5
    	4	6	10	40	20	12	8

18. 	11,0	11,5	12,0	12,5	13,0	13,5	14,0
    	5	10	30	25	15	10	5

19. 	124	164	204	244	284	324	364
    	5	15	40	25	8	4	3

	2,6	3,2	3,8	4,4	5,0	5,6	6,2
	5	15	40	23	8	4	3

21. 	106	156	206	256	306	356	406
    	8	10	60	12	5	3	2

22. 	12	14	16	18	20	22	24
    	4	6	10	40	20	12	8

23. 	13	15	17	19	21	23	25
    	5	10	30	25	15	10	5

24. 	130	140	150	160	165	170	175
    	2	8	12	30	20	18	10

	100	120	140	160	180	200	220
	3	9	15	41	27	10	5

2. Дані спостереження значень обслідуваної ознаки зведено в таблицю. Треба скласти варіаційний ряд і знайти: 1) моду; 2) медіану; 3) вибіркову середню; 4) вибіркове середнє квадратичне відхилення; 5) коефіцієнт варіації, асиметрію; 6) ексцес.

1. 15	21	24	16	21	24	17	21	24,1	24,2
   18	18,9	21,9	25	25,1	22	19,1	19,0	22,1	24,9
   22,2	19,9	20	23	25,9	26	23,1	20	20,2	22,9
   27,1	22,9	20,8	20,9	23,9	28	23	21,1	25	26,1

2. 18,1	20,5	21,2	21	20,2	20	18,6	19,6	20,7	20,7
   19,1	19,5	20,4	21,8	22	19,4	19,3	19,8	18,4	21,7
   19	19,6	20,9	20,4	19,4	19,3	20,1	18,9	21	20
   20,1	19,3	20,1	20,9	20,4	20,8	19,7	19,6	20	20,9
   21,8	22	19,6	20,1	22	19,8	20,3	21,7	19,1	18,5

1,5	2,1	2,4	1,6	2,1	2,4	1,7	2,1	2,41	2,42
1,8	1,89	2,19	2,5	2,51	2,2	1,91	1,9	2,21	2,49
2,22	19,9	2	2,3	2,59	2,60	2,31	2	2,02	2,29
2,71	2,29	2,07	2,09	2,39	2,8	2,3	2,11	2,5	2,61

4. 150	120	160	240	210	240	170	210	241	200
   202	229	271	229	207	209	242	180	189	219
   250	251	220	191	190	231	260	259	230	200
   199	222	249	221	280	211	230	250	261

5. 151	211	161	241	211	242	172	212	243	203
   205	230	274	231	209	211	245	187	220	251
   252	221	193	192	235	262	251	274	202	200
   223	200	223	282	211	230	251	263

40,4	40,5	40,6	40,4	40,6	40,4	40,1	40,3	40,2	40,3
40,1	40,9	40,8	40,2	40,5	40,6	40,5	40,0	40,1	40,2
40,4	40,8	40,5	40,1	40,4	40,5	40,4	40,7	40,4	40,4
40,8	40,5	40,0	40,6	40,3	40,6	40,4	40,1	40,6	40,4
40,1	40,6	40,4	40,7	40,6	40,7	40,4	40,5	40,2	40,5
40,4	40,5	40,6

7. 181	205	212	210	202	200	186	196	207	193
   201	189	210	200	201	203	207	191	195	204
   218	220	194	194	204	209	296	190	217	184
   198	193	201	209	204	208	191	185	197	196
   200	209	218	220	196	201	220	198	203	217

8. 404	405	404	405	406	404	401	403	402	403
   401	403	408	402	405	406	405	400	406	403
   406	404	408	405	401	404	405	404	407	404
   404	408	405	400	401	402	404	401	406	404
   407	406	407	404	403	402	405	403	404	405

1,81	2,05	2,12	2,10	2,02	2,00	1,86	1,96	2,07	1,96
2,09	2,04	1,94	1,94	2,20	2,18	2,04	1,95	1,93	2,01
1,89	2,10	2,00	2,01	2,03	2,07	1,91	1,91	1,95	1,97
1,96	2,00	2,09	2,18	2,20	1,96	2,01	2,20	1,98	2,03
2,17	1,90	2,17	1,84	1,98	1,93	2,01	2,09	2,04	2,08

10. 4,04	4,05	4,05	4,04	4,06	4,04	4,01	4,03	4,02	4,03
    4,01	4,03	4,08	4,02	4,05	4,06	4,05	4,00	4,06	4,03
    4,06	4,08	4,05	4,01	4,04	4,04	4,05	4,04	4,07	4,04
    4,04	4,08	4,05	4,00	4,01	4,02	4,04	4,01	4,06	4,04
    4,07	4,06	4,07	4,04	4,03	4,02	4,05	4,03	4,04	4,05

4	6	5	2	3	5	7	5	5	4
5	7	7	2	3	3	3	4	3	2
1	2	4	4	5	4	6	4	3	3
7	2	7	4	3	4	5	2	5	7
4	5	5	1	6	1	6	3	1	5
4	5	7	4	3	3	5	2	5	4
3	1	6	4	5	4	5	3	2	4

12. 5	7	6	3	4	6	8	6	6	5
    6	8	8	3	4	4	3	5	4	3
    2	3	5	5	6	5	7	5	4	4
    8	3	8	5	4	5	6	3	6	8
    5	6	6	2	7	2	7	4	2	6
    5	6	8	5	4	4	6	3	5	4
    2	7	5	6	5	6	4	3	5

6	8	7	4	5	7	9	7	7	6
7	9	9	4	5	4	5	6	5	4
3	4	6	6	7	6	8	6	5	5
9	4	9	6	5	6	7	4	7	9
6	7	7	3	8	3	8	5	3	7
6	7	9	6	5	5	7	4	7	6
5	3	8	6	7	6	7	5	4	6

14. 0,4	0,6	0,5	0,2	0,3	0,5	0,7	0,5	0,5	0,4
    0,5	0,7	0,7	0,2	0,3	0,2	0,3	0,4	0,3	0,2
    0,1	0,2	0,4	0,4	0,5	0,4	0,6	0,4	0,3	0,3
    0,7	0,2	0,7	0,4	0,3	0,4	0,5	0,2	0,5	0,7
    0,4	0,5	0,5	0,1	0,6	0,1	0,6	0,3	0,1	0,5
    0,4	0,5	0,7	0,4	0,3	0,3	0,5	0,2	0,5	0,4
    0,3	0,1	0,6	0,4	0,5	0,4	0,5	0,3	0,2	0,4

0,5	0,6	0,7	0,3	0,4	0,6	0,8	0,6	0,6	0,5
0,6	0,8	0,8	0,3	0,4	0,3	0,4	0,5	0,4	0,3
0,2	0,3	0,5	0,5	0,6	0,5	0,7	0,5	0,4	0,4
0,8	0,3	0,8	0,5	0,4	0,5	0,6	0,3	0,6	0,8
0,5	0,6	0,2	0,7	0,2	0,7	0,4	0,2	0,6	0,5
0,6	0,8	0,5	0,4	0,4	0,6	0,3	0,6	0,5	0,4
0,2	0,7	0,5	0,6	0,5	0,6	0,4	0,3	0,5

16. 0,6	0,8	0,6	0,4	0,5	0,7	0,9	0,7	0,7	0,6
    0,7	0,9	0,9	0,6	0,5	0,4	0,5	0,6	0,5	0,4
    0,3	0,4	0,6	0,6	0,7	0,6	0,8	0,6	0,5	0,5
    0,9	0,4	0,9	0,5	0,5	0,6	0,7	0,4	0,7	0,9
    0,6	0,7	0,7	0,3	0,7	0,3	0,8	0,5	0,3	0,7
    0,6	0,7	0,9	0,6	0,5	0,5	0,7	0,4	0,7	0,6
    0,4	0,4	0,8	0,6	0,7	0,6	0,7	0,5	0,4	0,6

40	60	50	20	30	50	70	50	50	40
50	70	70	20	30	20	10	20	40	40
50	40	60	40	30	30	70	20	70	40
30	40	50	20	50	70	40	50	50	10
60	10	60	30	10	50	40	50	70	40
30	30	50	20	50	40	30	10	60	40
50	40	50	30	20	40	30	40	50	40

18. 50	70	60	30	40	60	80	60	60	50
    60	80	80	30	40	30	20	30	50	50
    60	50	70	50	40	40	80	30	80	50
    40	50	60	30	60	80	50	60	60	20
    70	20	70	40	20	60	50	60	80	50
    40	40	60	30	60	50	40	20	70	50
    60	50	60	40	30	50	30	40	50	40

19. 130	140	149	151	159	177	177	178	200	240
    190	190	191	189	199	200	199	208	209	189
    201	202	203	210	230	211	231	210	241	182
    201	220	190	220	180	221	220	229	180	203
    218

13,0	14,0	14,9	15,1	15,9	17,7	17,7	17,8	20,0	24,0
19,0	19,0	19,1	18,9	19,9	20,0	19,9	20,0	20,8	20,9
18,9	20,1	20,3	21,0	23,0	21,1	23,1	21,0	24,1	18,2
20,1	22,0	19,0	22,0	18,0	22,1	22,0	22,9	18,0	20,3
21,8

21. 14,0	15,0	15,0	16,1	16,9	18,7	18,7	18,8	21,0	25,0
    20,0	20,0	20,1	19,9	20,9	21,0	20,9	21,8	21,9	19,9
    21,1	21,3	21,0	24,0	22,1	24,1	22,0	25,1	19,2	21,2
    23,0	20,0	23,0	19,0	23,1	23,0	23,9	19,0	21,3	22,3

22. 15,0	16,0	16,0	17,1	17,9	19,7	19,7	19,8	22,0	26,0
    21,0	21,0	21,1	20,9	21,9	22,0	21,9	22,8	22,9	20,9
    22,1	22,3	22,0	25,0	23,1	25,1	23,0	25,1	20,2	22,2
    24,0	21,0	24,0	20,0	24,1	24,0	24,0	20,0	22,3	23,8

23. 140	150	150	181	169	187	187	188	210	250
    200	200	201	199	209	210	209	218	219	199
    211	213	210	240	221	241	220	251	192	212
    230	200	230	190	231	230	239	190	213	228

24. 150	160	160	171	179	197	197	198	220	260
    210	210	211	209	219	220	219	228	229	209
    221	223	220	250	231	251	230	261	202	222
    240	210	240	200	241	240	249	200	223	238

1,50	1,60	1,60	1,71	1,79	1,97	1,97	1,98	2,20	2,60
2,10	2,10	2,11	2,09	2,19	2,20	2,19	2,28	2,29	2,09
2,21	2,23	2,20	2,50	2,31	2,51	2,30	2,61	2,02	2,22
2,40	2,10	2,40	2,00	2,41	2,40	2,49	2,00	2,23	2,38

3. Побудувати многокутник розподілу та нормальну криву для розподілу випадкової величини за такими даними:

1. 	330-350	350-370	370-390	390-410	410-430	430-450	450-470
   	1	9	38	36	33	8	5

2. 	320-340	340-360	360-380	380-400	400-420	420-440	440-460
   	2	8	36	38	35	6	5

	310-330	330-350	350-370	370-390	390-410	410-430	430-450
	1	9	38	36	33	8	5

4. 	290-310	310-330	330-350	350-370	370-390	390-410	410-430
   	2	8	36	38	35	6	5

5. 	270-290	290-310	310-330	330-350	350-370	370-390	390-410
   	1	9	38	36	33	8	5

6. 	250-270	270-290	290-310	310-330	330-350	350-370	370-390
   	1	9	38	36	33	8	5

7. 	250-270	270-290	290-310	310-330	330-350	350-370	370-390
   	2	8	36	38	35	6	5

	230-250	250-270	270-290	290-310	310-330	330-350	350-370
	2	8	36	38	35	6	5

9. 	32,5-33,5	33,5-34,5	34,5-35,5	35,5-36,5	36,5-37,5	37,5-38,5	38,5-39,5	39,5-40,5
   	3	9	16	24	29	15	3	1

10. 	33,5-34,5	34,5-35,5	35,5-36,5	36,5-37,5	37,5-38,5	38,5-39,5	39,5-40,5	40,5-41,5
    	3	9	16	24	29	15	3	1

11. 	34,5-35,5	35,5-36,5	36,5-37,5	37,5-38,5	38,5-39,5	39,5-40,5	40,5-41,5	41,5-42,5
    	3	9	16	24	29	15	3	1

12. 	35,5-36,5	36,5-37,5	37,5-38,5	38,5-39,5	39,5-40,5	40,5-41,5	41,5-42,5	42,5-43,5
    	5	7	14	26	27	17	3	1

	36,5-37,5	37,5-38,5	38,5-39,5	39,5-40,5	40,5-41,5	41,5-42,5	42,5-43,5	43,5-44,5
	1	11	18	22	27	17	3	1

14. 	37,5-38,5	38,5-39,5	39,5-40,5	40,5-41,5	41,5-42,5	42,5-43,5	43,5-44,5	44,5-45,5
    	4	8	15	25	28	16	2	2

15. 	38,5-39,5	39,5-40,5	40,5-41,5	41,5-42,5	42,5-43,5	43,5-44,5	44,5-45,5	45,5-46,5
    	5	7	14	26	27	17	3	1

16. 	6-8	8-10	10-12	12-14	14-16	16-18	18-20	20-22
    	1	18	30	69	75	38	14	5

17. 	5-7	7-9	9-11	11-13	13-15	15-17	17-19	19-21
    	2	17	31	68	76	37	13	6

	4-6	6-8	8-10	10-12	12-14	14-16	16-18	18-20
	3	16	32	67	77	36	12	7

19. 	7-9	9-11	11-13	13-15	15-17	17-19	19-21	21-23
    	4	15	33	66	78	35	11	8

20. 	0,5-0,7	0,7-0,9	0,9-1,1	1,1-1,3	1,3-1,5	1,5-1,7	1,7-1,9	1,9-2,1
    	5	14	34	65	79	34	15	4

21. 	0,6-0,8	0,8-1,0	1,0-1,2	1,2-1,4	1,4-1,6	1,6-1,8	1,8-2,0	2,0-2,2
    	2	17	31	68	76	37	13	6

22. 	0,4-0,6	0,6-0,8	0,8-1,0	1,0-1,2	1,2-1,4	1,4-1,6	1,6-1,8	1,8-2,0
    	1	18	30	69	75	38	14	5

	0,7-0,9	0,9-1,1	1,1-1,3	1,3-1,5	1,5-1,7	1,7-1,9	1,9-2,1	2,1-2,3
	3	16	32	69	77	37	12	7

24. 	1-3	3-5	5-7	7-9	9-11	11-13	13-15	15-17
    	4	15	33	66	78	35	11	8

	2-4	4-6	6-8	8-10	10-12	12-14	14-16	16-18
	5	14	34	65	79	34	15	4

4. Знайти довірчі інтервали для оцінки математичного сподівання нормального розподілу з надійністю 0,95, знаючи вибіркову середню , об’єм вибірки , та середнє квадратичне відхилення , якщо:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

25. 

4. Задані вибіркові середні і , знайдені по вибіркам обсягом і , добутим з нормальних генеральних сукупностей і з відповідними дисперсіями і 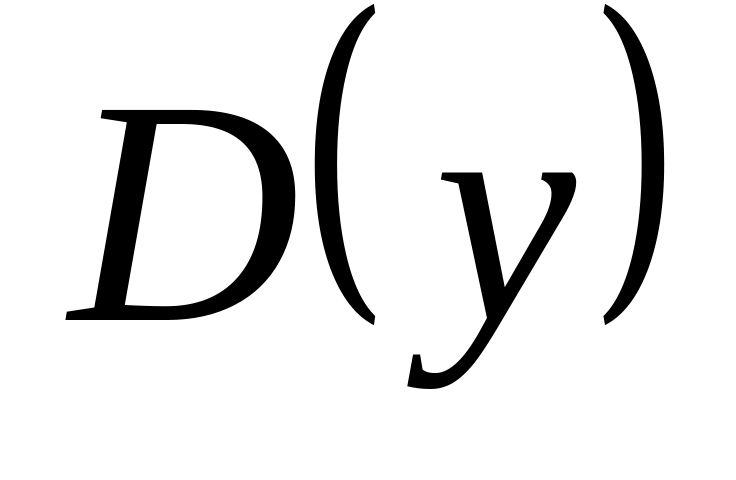. Треба при рівні значимості перевірити нульову гіпотезу за конкуруючою гіпотезою 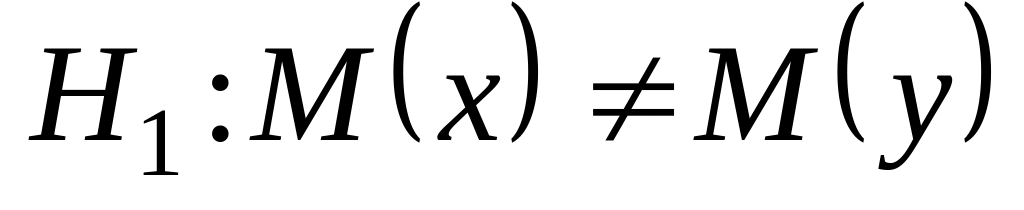, тобто встановити значимо чи не значимо відрізняються вибіркові середні, якщо:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

25. 

4. Треба при рівні значимості перевірити по критерію узгодженості Пірсона гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні частоти та теоретичні частоти :

1. 	6	10	20	27	19	12	6
   	5	14	16	25	21	12	7

2. 	4	12	18	29	17	14	6
   	5	14	15	26	18	14	8

	8	10	18	27	17	11	9
	4	15	16	25	21	12	7

4. 	4	15	16	25	21	12	7
   	5	11	22	25	21	11	5

5. 	5	13	17	25	21	12	7
   	4	15	15	28	20	14	6

6. 	7	12	16	25	21	11	7
   	5	12	18	29	20	10	6

7. 	8	12	16	27	19	12	6
   	5	17	13	25	21	12	7

8. 	6	15	16	26	19	12	6
   	5	17	13	25	21	12	7

	6	13	21	23	19	12	6
	5	14	16	25	21	13	6

10. 	5	11	20	27	19	12	6
    	6	13	16	25	20	13	7

11. 	6	9	21	27	20	11	6
    	5	13	17	25	21	12	7

12. 	2	13	15	26	22	13	9
    	3	11	14	28	21	14	9

13. 	3	11	14	28	21	13	10
    	2	13	15	26	22	15	7

14. 	3	12	15	28	23	12	7
    	3	14	16	29	20	15	3

	3	14	16	29	20	14	4
	4	12	15	28	22	12	7

16. 	4	10	18	27	23	12	6
    	3	12	19	26	22	11	7

17. 	4	11	17	26	22	13	7
    	4	10	18	27	23	11	7

18. 	4	12	18	29	17	14	6
    	5	14	15	26	18	14	8

19. 	4	13	20	26	18	12	7
    	4	15	15	28	20	14	6

20. 	7	9	20	24	22	13	5
    	7	11	18	22	19	14	9

	5	14	15	26	22	10	8
	3	14	17	30	21	9	6

22. 	7	13	18	25	20	12	6
    	4	18	15	23	22	12	7

23. 	5	13	17	26	20	13	6
    	5	16	18	24	18	13	8

24. 	4	15	17	24	19	15	6
    	4	12	22	25	17	14	6

	5	10	21	27	20	11	6
	4	14	17	26	20	12	7

4. Знайти вибіркове рівняння прямої 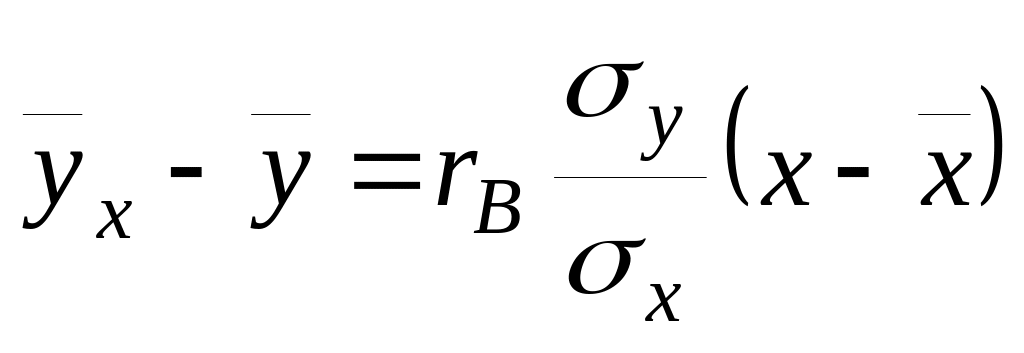регресії на за даною кореляційною таблицею:

	5	10	15	20	25	30
45	2	4	–	–	–	–	6
55	–	3	5	–	–	–	8
65	–	–	5	35	5	–	45
75	–	–	2	8	17	–	27
85	–	–	–	4	7	3	14
	2	7	12	47	29	3

2)

	10	15	20	25	30	35
40	2	4	–	–	–	–	6
50	–	3	7	–	–	–	10
60	–	–	5	30	10	–	45
70	–	–	7	10	8	–	25
80	–	–	–	5	6	3	14
	2	7	19	45	24	3

3)

	15	20	25	30	35	40
15	4	1	–	–	–	–	5
25	–	6	4	–	–	–	10
35	–	–	2	50	2	–	54
45	–	–	1	9	7	–	17
55	–	–	–	4	3	7	14
	4	7	7	63	12	7

4)

	2	7	12	17	22	27
100	1	5	–	–	–	–	6
120	–	5	3	–	–	–	8
130	–	–	3	40	12	–	55
140	–	–	2	10	5	–	17
150	–	–	–	3	4	7	14
	1	10	8	53	21	7

5)

	5	10	15	20	25	30
10	3	5	–	–	–	–	8
20	–	4	4	–	–	–	8
30	–	–	7	35	8	–	50
40	–	–	2	10	8	–	20
50	–	–	–	5	6	3	14
	3	9	13	50	22	3

6)

	12	17	22	27	32	37
25	2	4	–	–	–	–	6
35	–	6	3	–	–	–	9
45	–	–	6	35	4	–	45
55	–	–	2	8	6	–	16
65	–	–	–	14	7	3	24
	2	10	11	57	17	3

7)

	15	20	25	30	35	40
25	2	4	–	–	–	–	6
35	–	3	5	–	–	–	8
45	–	–	5	35	5	–	45
55	–	–	2	8	17	–	27
65	–	–	–	4	7	3	14
	2	7	12	47	29	3

8)

	4	9	14	19	24	29
30	3	3	–	–	–	–	6
40	–	5	4	–	–	–	9
50	–	–	40	2	8	–	50
60	–	–	5	10	6	–	21
70	–	–	–	4	7	3	14
	3	8	49	16	21	3

9)

	5	10	15	20	25	30
30	2	6	–	–	–	–	8
40	–	5	3	–	–	–	8
50	–	–	7	40	2	–	49
60	–	–	4	9	6	–	19
70	–	–	–	4	7	5	16
	2	11	14	53	15	5

10)

	10	15	20	25	30	35
20	5	1	–	–	–	–	6
30	–	6	2	–	–	–	8
40	–	–	5	40	5	–	50
50	–	–	2	8	7	–	17
60	–	–	–	4	7	8	19
	5	7	9	52	19	8

11)

	10	20	30	40	50	60
10	1	2	–	–	–	–	3
20	–	3	4	–	–	–	7
30	–	–	5	45	4	–	54
40	–	–	2	7	3	–	12
50	–	–	–	4	14	6	24
	1	5	11	56	21	6

12)

	10	15	20	25	30	35
20	2	3	–	–	–	–	5
25	–	4	3	1	–	–	8
30	–	–	5	46	7	–	58
35	–	–	1	8	4	–	13
40	–	–	–	3	7	6	16
	2	7	9	58	18	6

13)

	5	15	25	35	45	55
10	3	4	–	–	–	–	7
30	–	4	5	–	–	–	9
50	–	–	2	47	8	–	57
70	–	–	–	6	8	1	15
90	–	–	–	6	3	3	12
	3	8	7	59	19	4

14)

	6	12	18	24	30	36
5	4	5	–	–	–	–	9
15	–	5	6	–	–	–	11
25	–	–	5	48	7	–	60
35	–	–	5	4	3	–	12
45	–	–	–	–	5	3	8
	4	10	16	52	15	3

15)

	7	14	21	28	35	42
10	5	6	–	–	–	–	11
25	–	6	7	–	–	–	13
40	–	–	–	49	2	–	60
55	–	–	–	5	7	–	14
70	–	–	–	–	–	2	2
	5	12	18	54	9	2

16)

	2	12	22	32	42	52
5	1	5	–	–	–	–	6
10	–	2	3	–	–	–	5
15	–	–	7	55	1	–	63
20	–	–	5	4	7	–	18
25	–	–	–	3	3	2	8
	1	7	12	62	11	2

17)

	3	11	19	27	35	43
5	2	4	–	–	–	–	6
15	–	3	3	–	–	–	6
25	–	–	6	56	1	–	63
35	–	–	2	6	8	–	16
45	–	–	–	1	6	2	8
	2	7	11	63	15	2

18)

	4	14	24	34	44	54
5	3	3	–	–	–	–	6
25	–	4	4	–	–	–	8
45	–	–	5	55	1	–	61
65	–	–	1	5	8	–	14
85	–	–	–	2	8	1	11
	3	7	10	62	17	1

19)

	5	20	35	50	65	80
5	4	2	–	–	–	–	6
35	–	5	3	–	–	–	8
65	–	–	6	58	1	–	65
95	–	–	5	4	9	–	18
125	–	–	–	1	1	1	3
	4	7	14	63	11	1

20)

	6	16	26	36	46	56
5	5	1	–	–	–	–	6
20	–	6	2	1	–	–	9
35	–	–	8	45	2	–	55
50	–	–	4	7	7	–	18
65	–	–	–	5	4	3	12
	5	7	14	58	13	3

21)

	7	14	21	28	35	42
10	5	1	–	–	–	–	6
15	–	6	5	–	–	–	11
20	–	–	6	35	9	–	50
25	–	–	8	9	2	–	19
30	–	–	–	7	1	6	14
	5	7	19	51	11	6

22)

	7	14	21	28	35	42
10	4	2	–	–	–	–	6
25	–	5	12	–	–	–	17
40	–	–	5	45	10	–	60
55	–	–	3	8	2	–	17
70	–	–	–	2	1	1	4
	4	7	20	55	13	1

23)

	13	19	25	31	37	44
20	3	3	–	–	–	–	6
25	–	4	5	1	–	–	10
30	–	–	4	55	7	–	66
35	–	–	3	3	8	–	14
40	–	–	–	–	–	4	4
	3	7	12	59	15	4

24)

	7	14	21	28	35	42
20	2	4	–	–	–	–	6
30	–	3	6	–	–	–	9
40	–	–	3	65	–	–	68
50	–	–	–	2	11	–	13
60	–	–	–	–	–	4	4
	2	7	9	67	11	4

25)

	15	24	33	42	51	60
20	1	5	–	–	–	–	6
35	–	2	8	–	–	–	10
50	–	–	2	51	7	2	62
65	–	–	–	2	10	–	12
80	–	–	–	–	–	10	10
	1	7	10	53	17	12