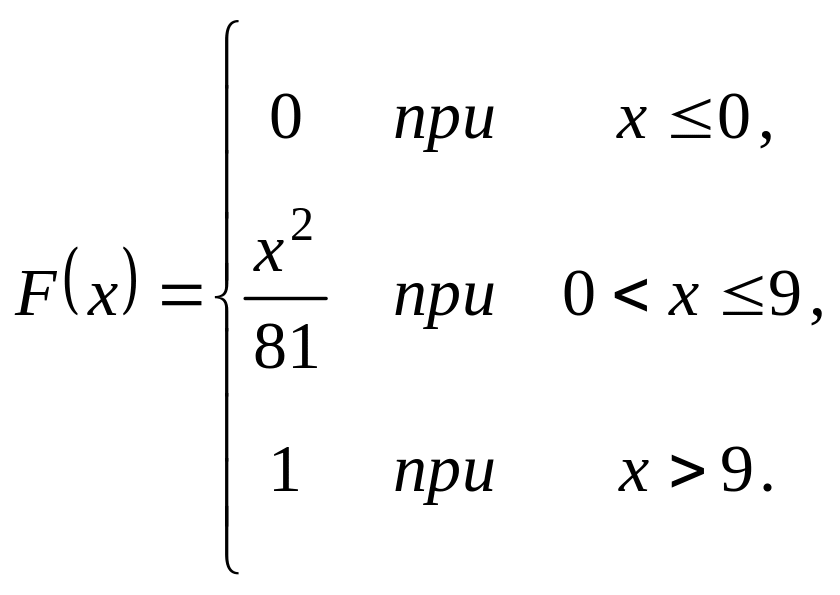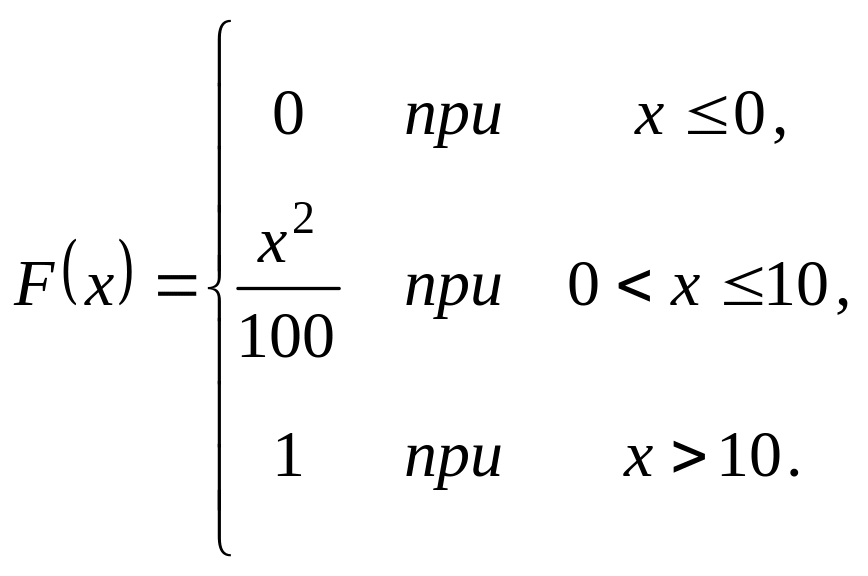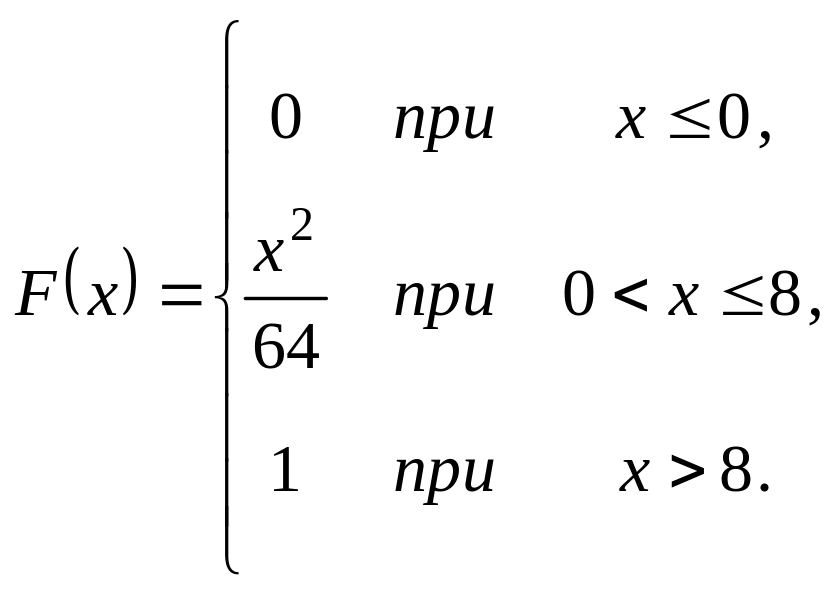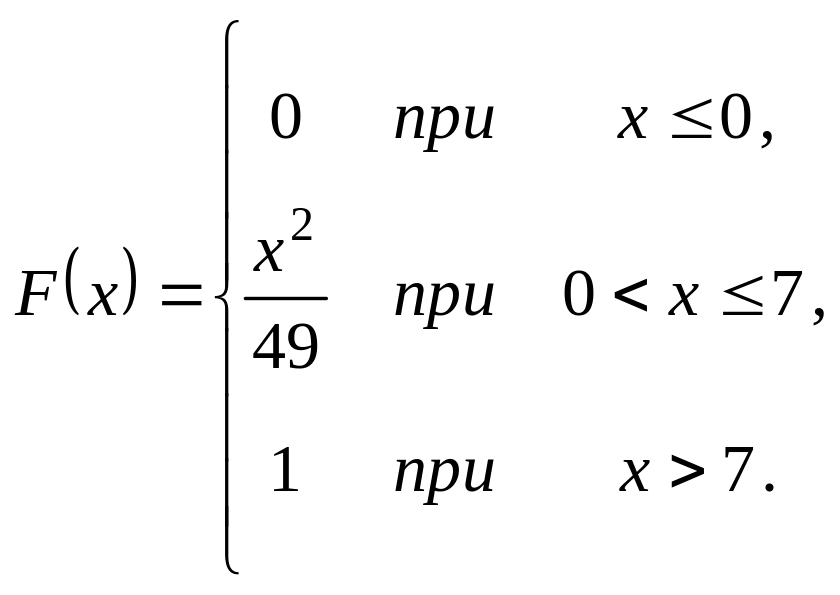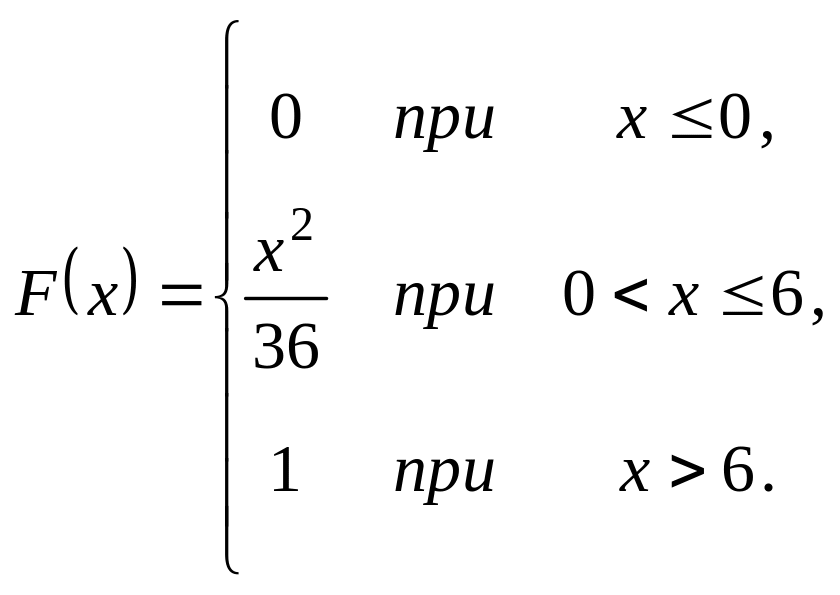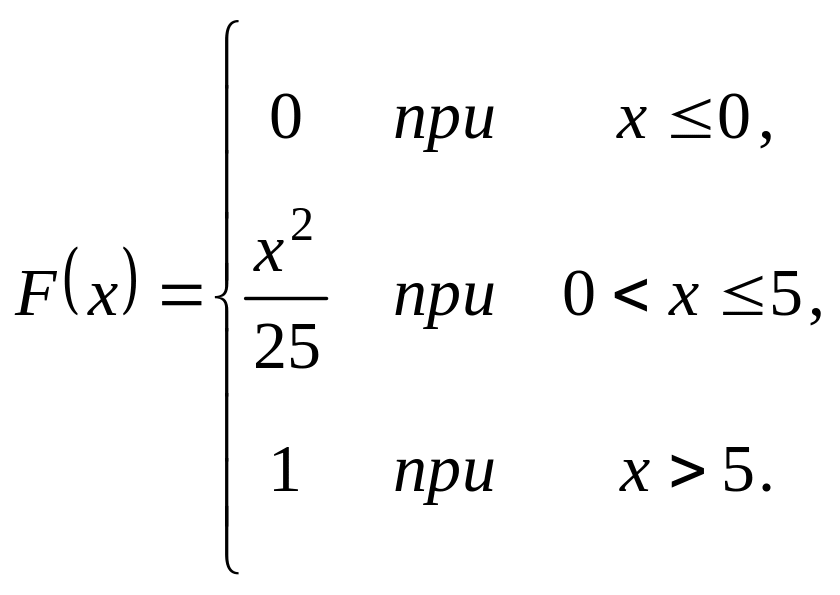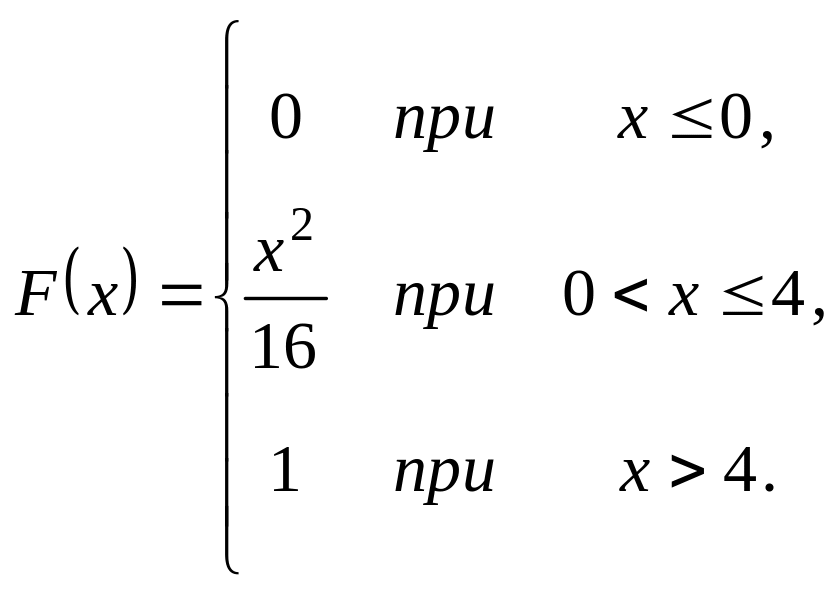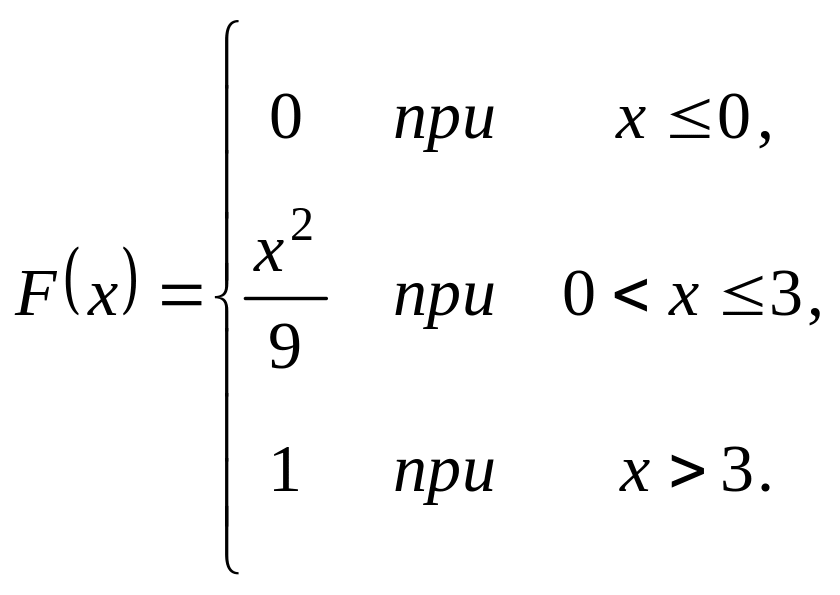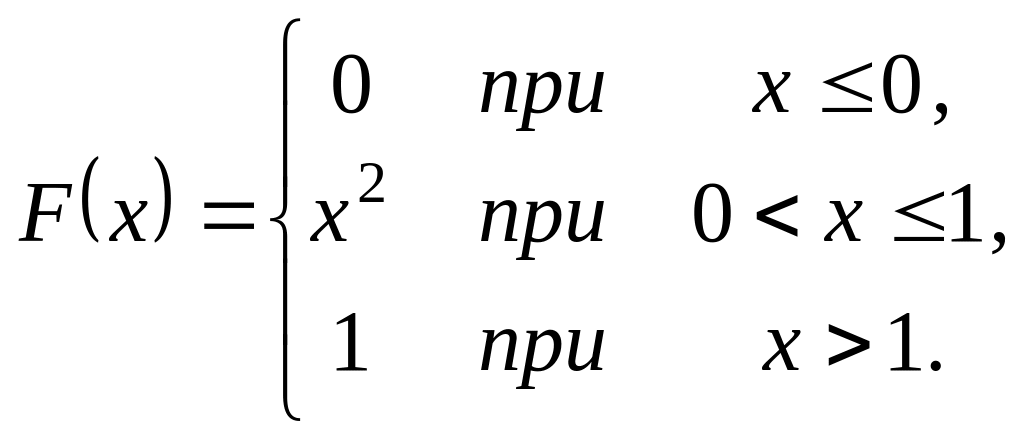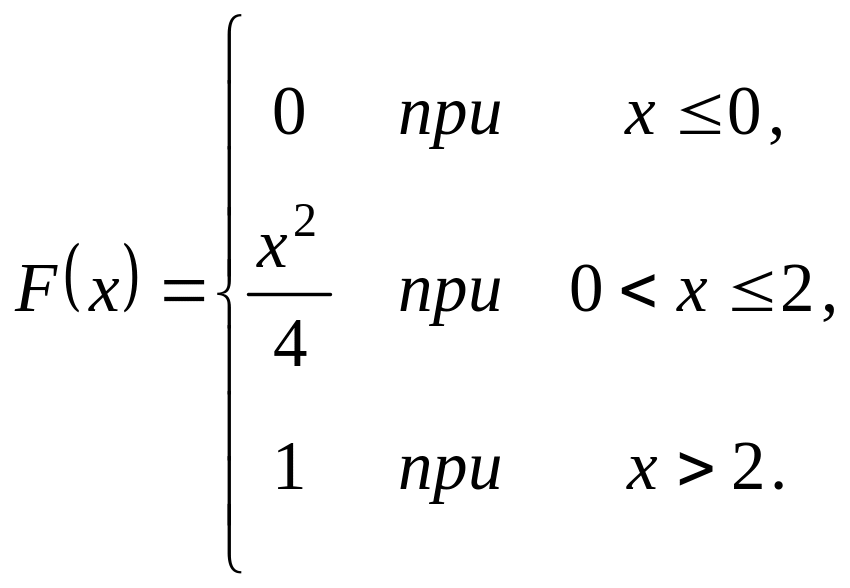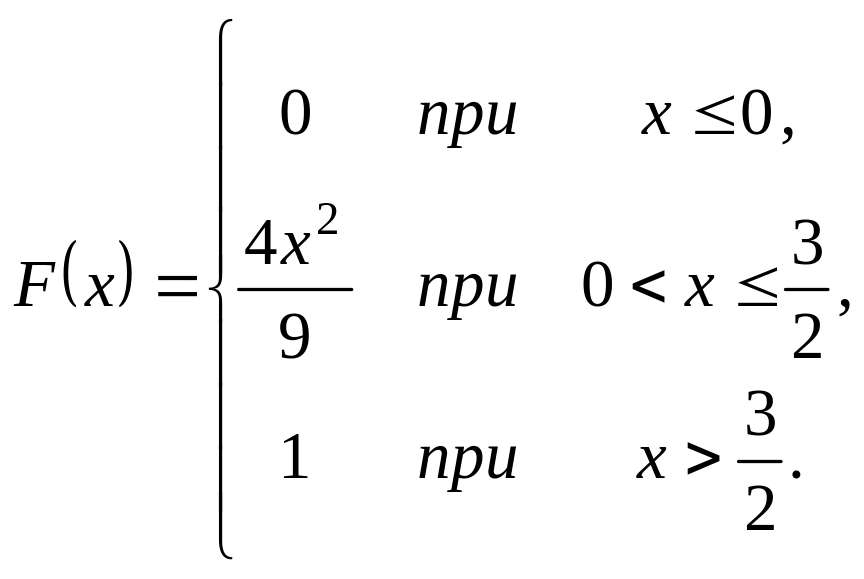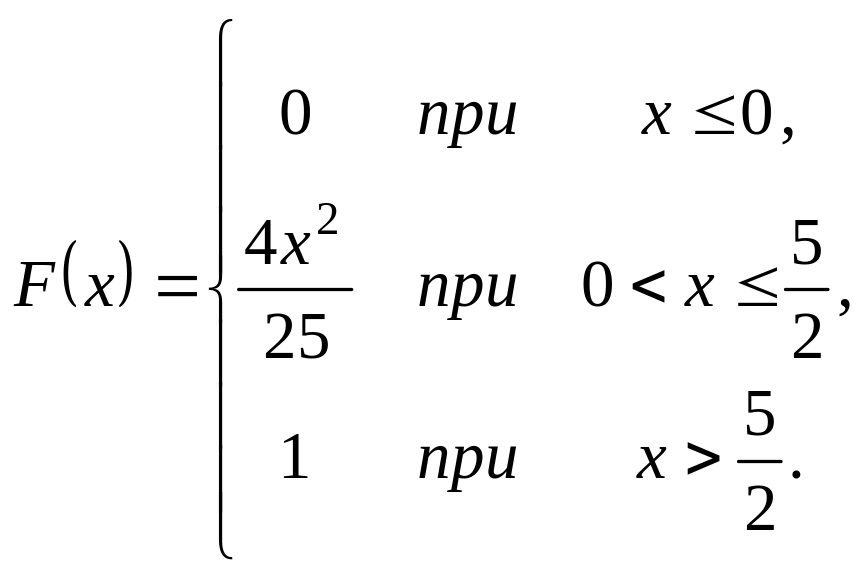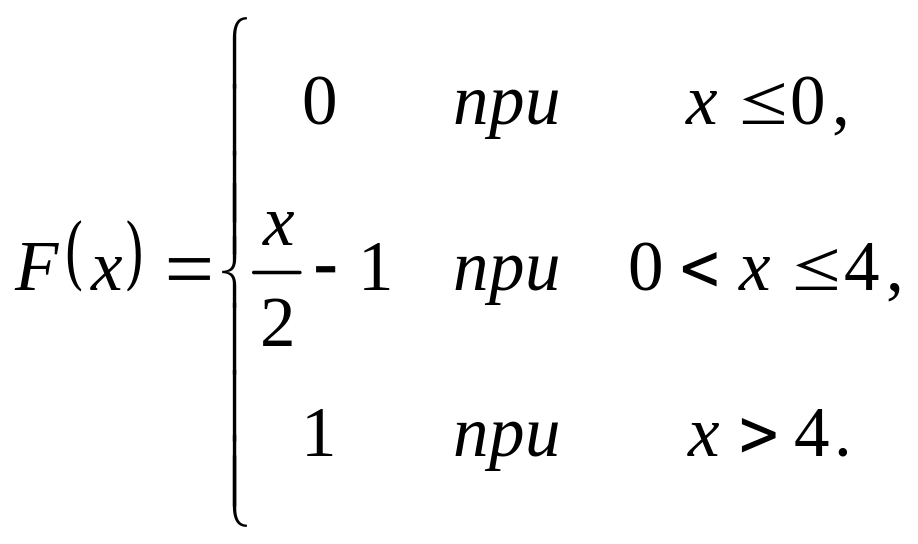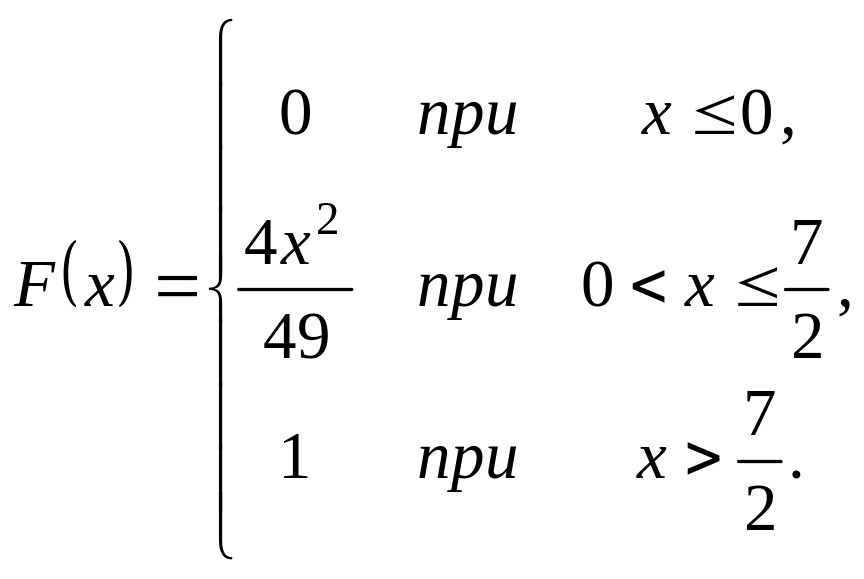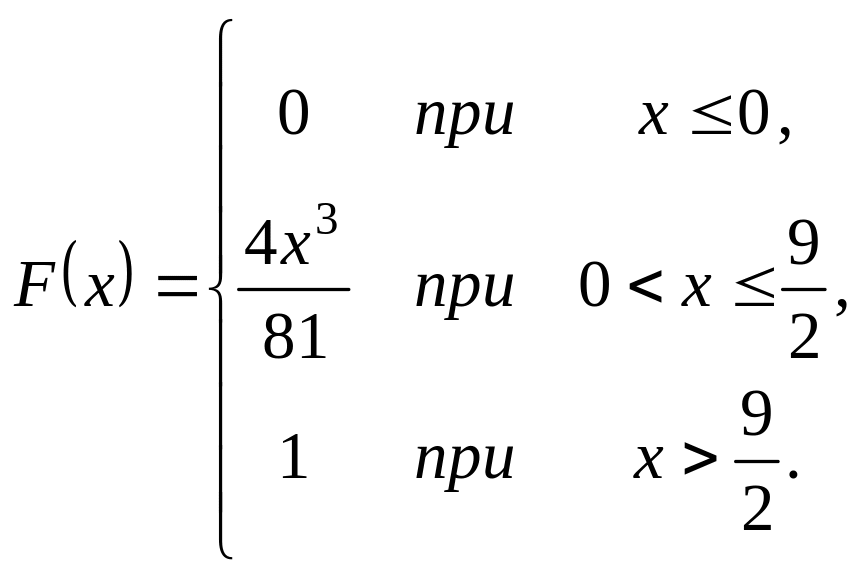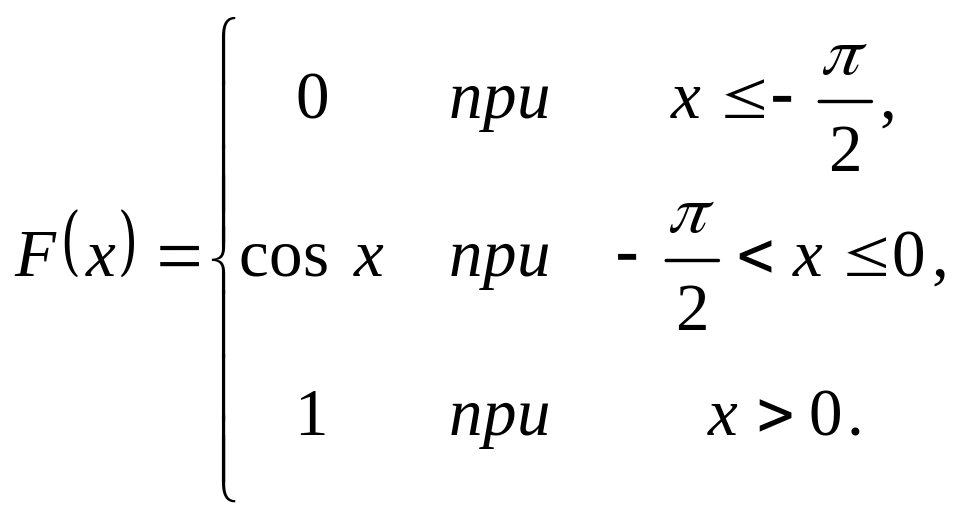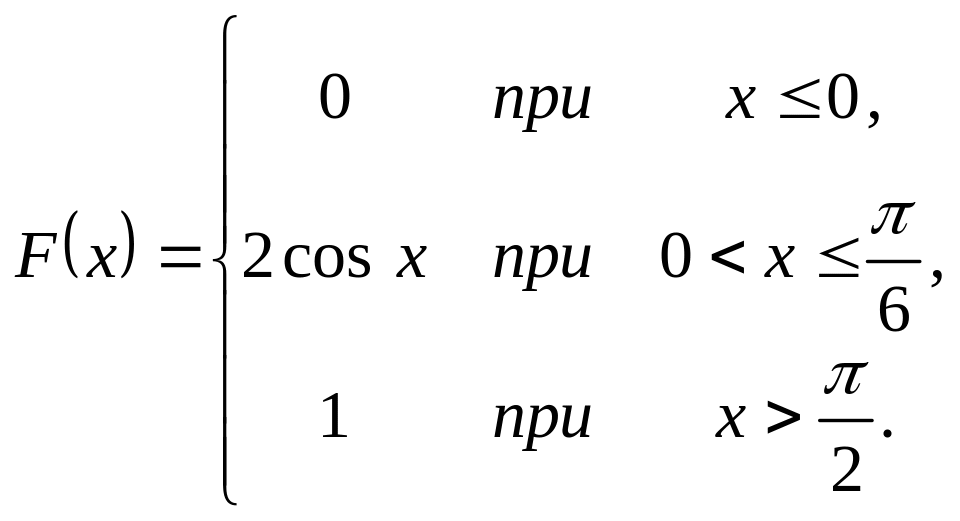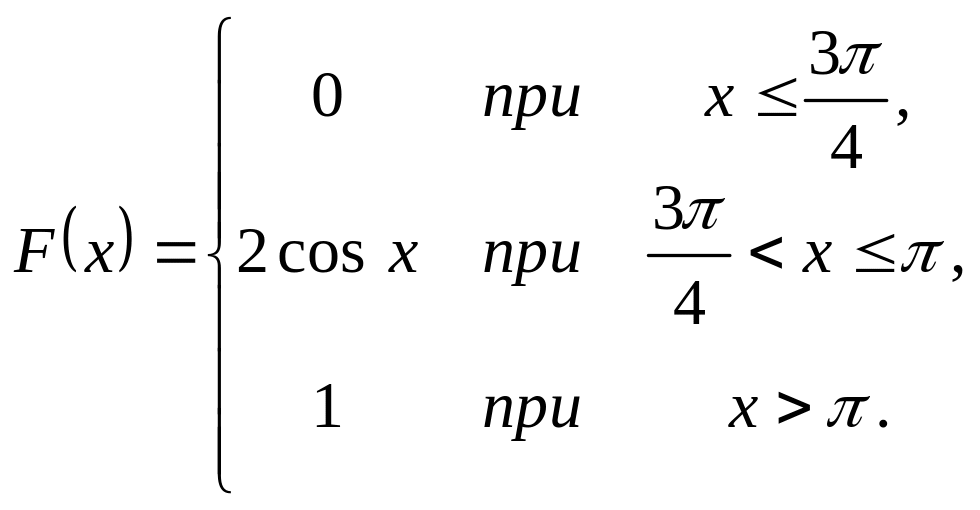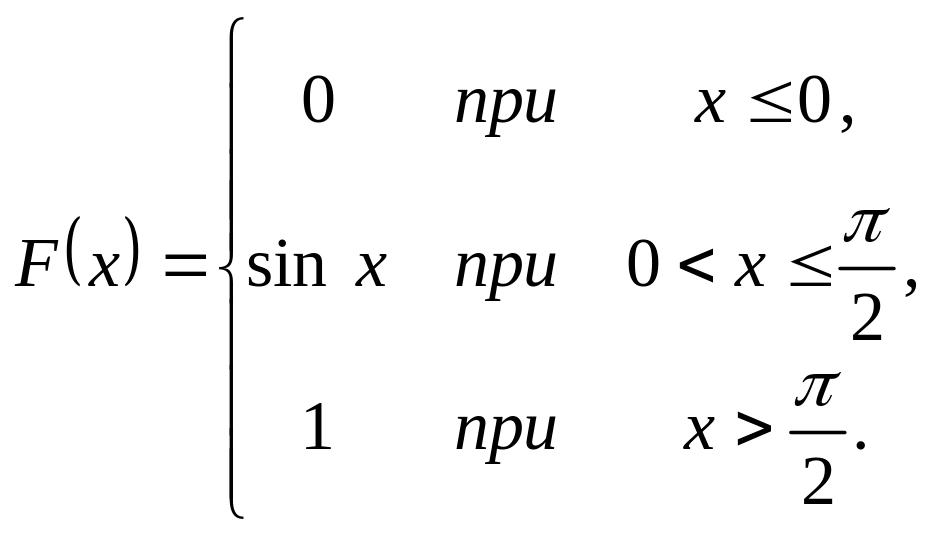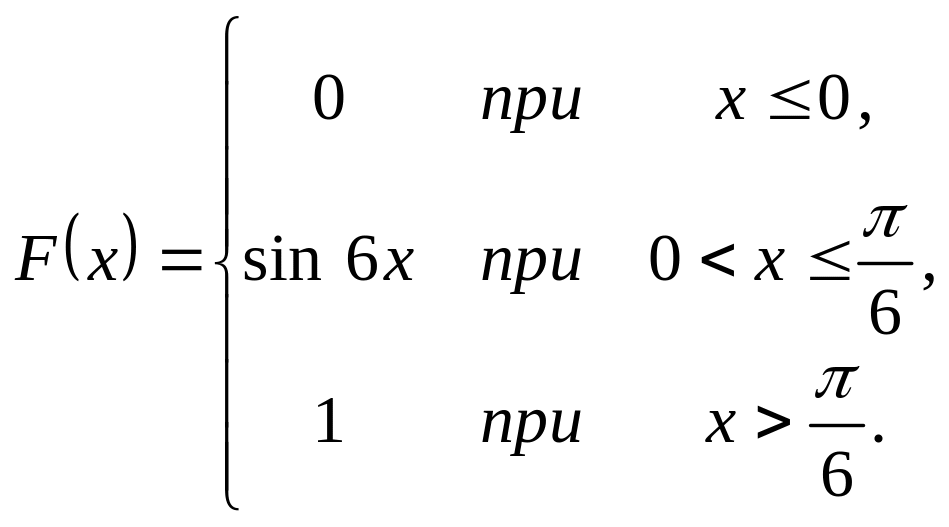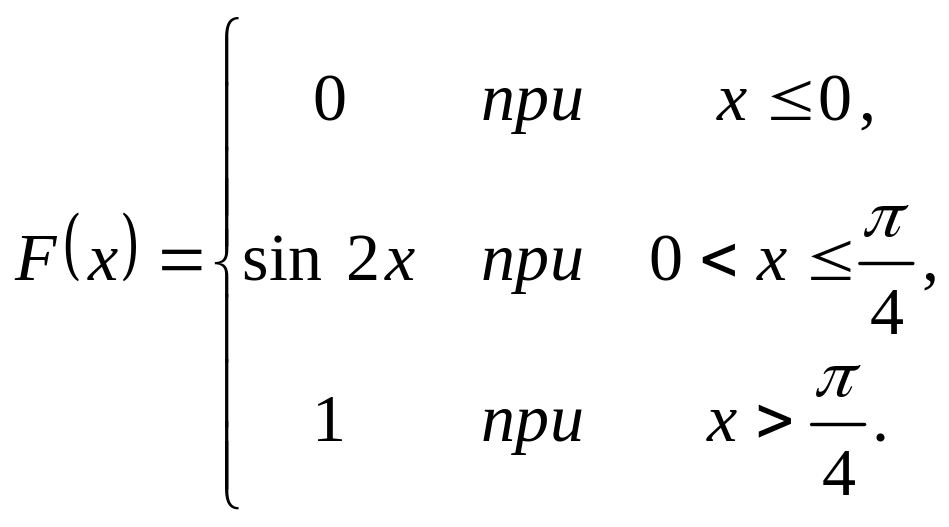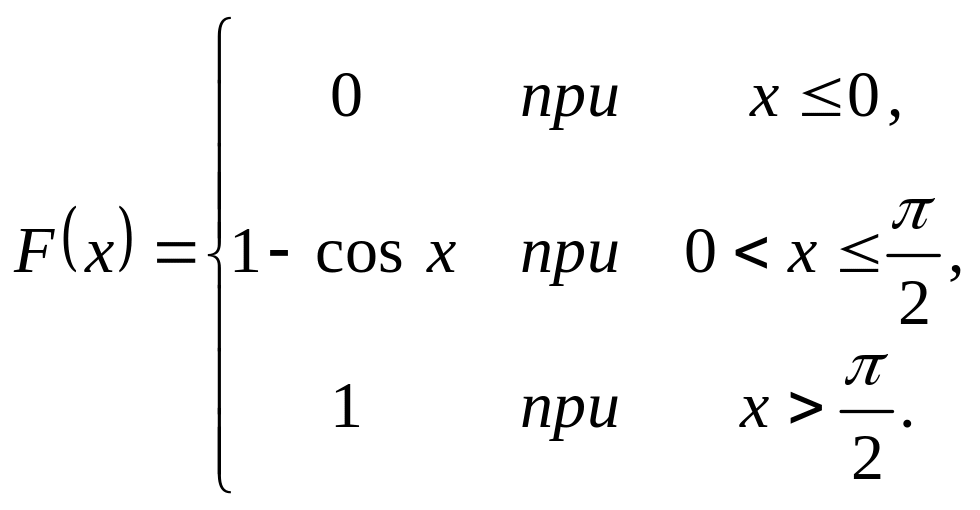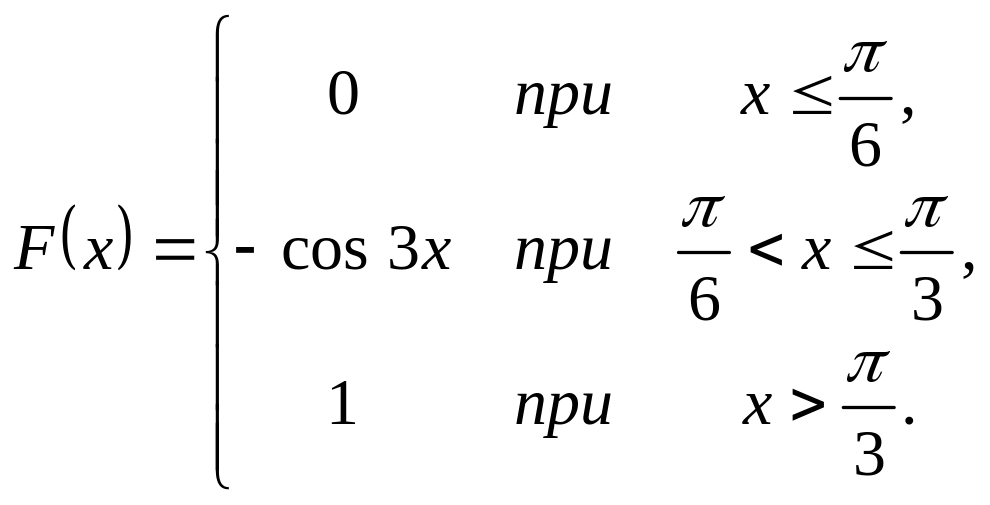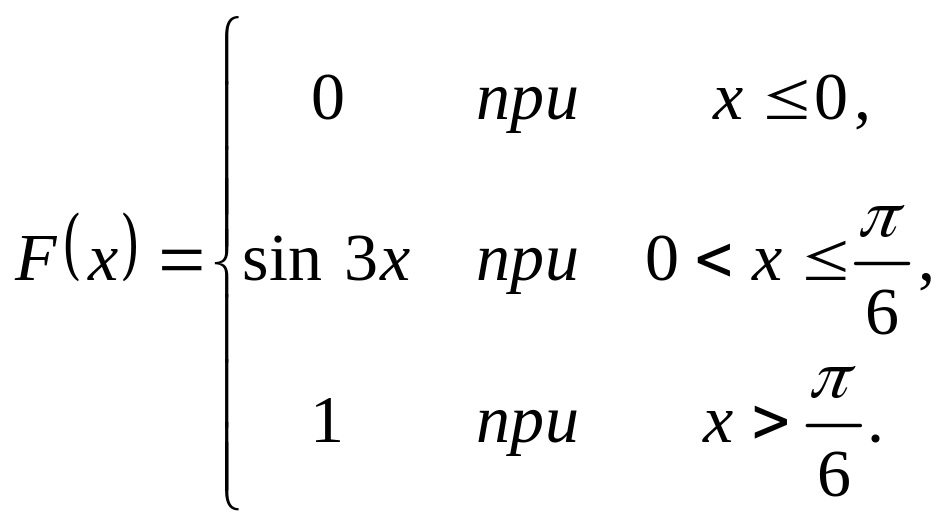- •Програма Частина 1. Теорія ймовірностей. Розділ 1. Випадкові події.
- •Розділ 2. Випадкові величини.
- •Розділ 3. Система двох випадкових величин.
- •Частина 2. Елементи математичної статистики. Розділ 1. Вибірковий метод.
- •Розділ 2. Статистичні оцінки параметрів розподілу.
- •Розділ 3. Елементи теорії кореляції.
- •Розділ 4. Статистична перевірка статистичних гіпотез.
- •Геометричні ймовірності
- •Основні теореми Теореми додавання та множення ймовірностей
- •Ймовірність появи хоча б однієї події
- •Локальна та інтегральна теореми Лапласа
- •Відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях
- •Найімовірніше число появ події в незалежних випробуваннях
- •Числові характеристики дискретних випадкових величин
- •Теоретичні моменти
- •Закон великих чисел Нерівність Чебишева
- •Теорема Чебишева
- •Функції розподілу ймовірностей випадкових величин Інтегральна функція розподілу ймовірностей випадкової величини
- •Диференціальна функція розподілу ймовірностей неперервної випадкової величини
- •Числові характеристики неперервних випадкових величин
- •Рівномірний розподіл
- •Нормальний розподіл
- •Показовий розподіл та його числові характеристики
- •Функція надійності
- •Розділ 3. Системи двох випадкових величин Закон розподілу двовимірної випадкової величини
- •Числові характеристики неперервної системи двох випадкових величин
- •Частина 2. Елементи математичної статистики Розділ 1. Вибірковий метод Статистичний розподіл вибірки
- •Емпірична функція розподілу
- •Полігон та гістограма а. Дискретний розподіл ознаки
- •Б. Неперервний розподіл ознаки
- •Розділ 2. Статистичні оцінки параметрів розподілу Точкові оцінки
- •Інтервальні оцінки
- •Методи розрахунку зведених характеристик вибірки Метод добутків обчислення вибіркових середньої та дисперсії Рівновіддалені варіанти
- •Асиметрія та ексцес емпіричного розподілу
- •Розділ 3. Елементи теорії кореляції Лінійна кореляція
- •Варіанти контрольної роботи Частина 1. Теорія ймовірностей
- •Частина 2. Математична статистика
- •Література
Розділ 3. Елементи теорії кореляції Лінійна кореляція
Якщо обидві лінії регресії на та на – прямі, то кореляцію називають лінійною.
Вибіркове рівняння прямої лінії регресії на має вигляд
![]()
де
![]() – умовна середня;
– умовна середня;
![]() і
і
![]() – вибіркові середні ознак
та
;
– вибіркові середні ознак
та
;
![]() та
та
![]() – вибіркові середні квадратичні
відхилення;
– вибіркові середні квадратичні
відхилення;
![]() – вибірковий коефіцієнт кореляції,
причому
– вибірковий коефіцієнт кореляції,
причому
![]()
Вибіркове рівняння прямої лінії регресії на має вигляд:
![]()
Якщо дані спостереження над ознаками та задані у вигляді кореляційної таблиці з рівновіддаленими варіантами, то доцільно перейти до умовних варіант
![]()
де
![]() – «хибний нуль» варіант
(новий початок відліку); в якості хибного
нуля вигідно прийняти варіанту, яка
розташована приблизно в середині
варіаційного ряду (умовимося брати в
якості хибного нуля варіанту, яка має
найбільшу частоту);
– «хибний нуль» варіант
(новий початок відліку); в якості хибного
нуля вигідно прийняти варіанту, яка
розташована приблизно в середині
варіаційного ряду (умовимося брати в
якості хибного нуля варіанту, яка має
найбільшу частоту);
![]() – крок, тобто різниця між двома сусідніми
варіантами
;
– крок, тобто різниця між двома сусідніми
варіантами
;
![]() – хибний нуль варіант
;
– хибний нуль варіант
;
![]() – крок варіант
.
– крок варіант
.
У цьому випадку вибірковий коефіцієнт кореляції
![]()
причому
доданок
![]() зручно обчислювати, використовуючи
розрахункову таблицю.
зручно обчислювати, використовуючи
розрахункову таблицю.
Величини
![]() ,
,
![]() ,
,
![]() ,
,
![]() можуть бути знайдені або методом добутків
(при великому числі даних), або безпосередньо
за формулами:
можуть бути знайдені або методом добутків
(при великому числі даних), або безпосередньо
за формулами:
![]()
Знаючи
ці величини, можна визначити, величини
![]() и
и
![]() ,
що входять у рівняння регресії за
формулами:
,
що входять у рівняння регресії за
формулами:
![]()
Для
оцінки сили лінійного кореляційного
зв'язку служить вибірковий коефіцієнт
кореляції
![]() чим ближче
чим ближче
![]() до одиниці, тим зв'язок сильніше; чим
ближче
до нуля, тим зв'язок слабший.
до одиниці, тим зв'язок сильніше; чим
ближче
до нуля, тим зв'язок слабший.
Варіанти контрольної роботи Частина 1. Теорія ймовірностей
Розвя’зати задачу.
Студент знає 45 питань програми. Кожний екзаменаційний білет складається з трьох питань. Знайти ймовірність того, що студент знає: а) всі три питання; б) тільки два питання; в) тільки одне питання екзаменаційного білету.
У кожному з двох кошиків знаходиться 5 білих і 10 чорних куль. З першого кошика переклали в другий навмання одну кулю, а потім із другого кошика витягли навмання одну кулю. Знайти ймовірність того, що куля, яку витягли, буде чорною.
Три стрільці в однакових і незалежних умовах зробили по одному пострілу по одній і тій же цілі. Ймовірність влучення у неї першим стрільцем дорівнює 0,9; другим – 0,8; третім – 0,7. Знайти ймовірність того, що: а) тільки один стрілець влучив у ціль; б) тільки два стрільці влучили в ціль; в) всі стрільці влучили в ціль.
Ймовірність того, що подія настане в кожному з однакових і незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що в 1600 випробуваннях подія настане 1200 разів.
Для сигналізації про аварію встановлено три незалежно працюючих пристрої. Ймовірність того, що при аварії спрацює перший пристрій дорівнює 0,9; другий – 0,95; третій – 0,85. Знайти ймовірність того, що при аварії спрацює: а) тільки один пристрій; б) тільки два пристрої; в) всі три пристрої.
Ймовірність настання події у кожному з однакових і незалежних випробувань дорівнює 0,02. Знайти ймовірність того, що в 150 випробуваннях подія настане 5 разів.
У партії з 1000 виробів є 10 дефектних. Знайти ймовірність того, що серед 50 виробів, взятих навмання із цієї партії, рівно три вироби будуть дефектними.
Ймовірність настання події у кожному з однакових і незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що в 125 випробуваннях подія настане не менше 75 і не більше 90 разів.
На трьох верстатах з однаковими і незалежними умовами готуються деталі одного і того ж найменування. На першому верстаті виготовляють 10%, на другому – 30%, на третьому – 60% усіх деталей. Ймовірність того, що кожна деталь буде бездефектною дорівнює 0,7, якщо вона виготовлена на першому верстаті, 0,8 – якщо на другому верстаті і 0,9 – якщо на третьому верстаті. Знайти ймовірність того, що навмання взята деталь буде бездефектною.
Два брати знаходяться у складі двох спортивних команд по 12 осіб у кожній. У двох кошиках є 12 білетів із номерами від 1 до 12. Члени кожної команди виймають навмання білети з визначеного кошика (без повернення). Знайти ймовірність того, що обидва брати витягнуть білет із номером 6.
З трьох гармат провели залп по цілі. Ймовірність попадання при одному пострілі з першої гармати дорівнює 0,8; для другої та третьої гармати ця ймовірність відповідно дорівнює 0,7 і 0,9. Знайти ймовірність того, що: а) тільки один снаряд влучить у ціль; б) тільки два снаряди влучать у ціль; в) всі снаряди влучать у ціль; г) хоча б один снаряд влучить у ціль.
Три стрільці зробили залп по цілі. Ймовірність влучення у ціль першим стрільцем дорівнює 0,7; для другого і третього стрільців ця ймовірність відповідно дорівнює 0,8 і 0,9. Знайти ймовірність того, що: а) тільки один стрілець влучить у ціль; б) тільки два стрільці влучать у ціль; в) усі три стрільці влучать у ціль; г) хоча б один стрілець влучить у ціль.
Студент знає 50 з 60 питань програми. Знайти ймовірність того, що студент знає 2 питання, що знаходяться у його екзаменаційному білеті.
Дві команди з 10 спортсменів виконують жеребкування для присвоєння номерів учасникам змагань. Два брати входять у склад різних команд. Знайти ймовірність того, що обидва брати будуть значитись під номером 5.
Два стрільці зробили по одному пострілу в мішень. Ймовірність влучення в мішень кожним стрільцем дорівнює 0,8. Знайти ймовірність того, що: а) обидва стрільці влучать у мішень; б) обидва стрільці не влучать у мішень; в) тільки один стрілець влучить у мішень; г) хоча б один стрілець влучить у мішень.
Ймовірність хоча б одного влучення у мішень при двох пострілах дорівнює 0,96. Знайти ймовірність трьох влучень у мішень.
Експедиція видавництва відправила газети у два поштових відділення. Ймовірність своєчасної доставки газет у кожне відділення пошти дорівнює 0,9. Знайти ймовірність того, що: а) обидва поштові відділення одержать газети своєчасно; б) обидва поштові відділення одержать газети із запізненнями; в) тільки одне відділення одержить газети своєчасно; г) хоча б одне відділення одержить газети своєчасно.
У кожному з двох кошиків знаходиться 2 чорних і 8 білих куль. З першого кошика навмання взята куля і перекладена в другий кошик, після чого з другого кошика навмання витягнули кулю. Знайти ймовірність того, що куля, витягнута з другого кошика, буде чорною.
Дві перфокартощиці набили однакові комплекти перфокарт. Ймовірність того, що перша перфокартощиця зробить помилку дорівнює 0,05; для другої перфокартощиці ця ймовірність дорівнює 0,1. При перевірці перфокарт виявилась помилка. Знайти ймовірність того, що помилилася перша перфокартощиця.
Ймовірність появи події у кожному з незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що в 100 випробуваннях подія настане не менше 70 і не більше 80 разів.
Ймовірність появи події у кожному з незалежних випробувань дорівнює 0,2. Знайти ймовірність того, що подія настане 20 разів в 100 випробуваннях.
Ймовірність появи події у кожному з незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що подія настане 130 разів в 144 випробуваннях.
У кожному з двох кошиків міститься 4 чорних і 6 білих куль. З другого кошика навмання витягли кулю і переклали в перший, після чого з першого кошика взяли кулю. Знайти ймовірність того, що ця куля біла.
Ймовірність появи події у кожному з незалежних випробувань дорівнює 0,8. Скільки потрібно провести випробувань, щоб із ймовірністю 0,95 можна було чекати, що відхилення відносної частоти появи події від її ймовірності не більше ніж 0,02.
Ймовірність появи події у кожному з незалежних випробувань дорівнює 0,2. Проведено 900 випробувань. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності не більше ніж на 0,04.
Дискретна випадкова величина може набувати тільки два значення:
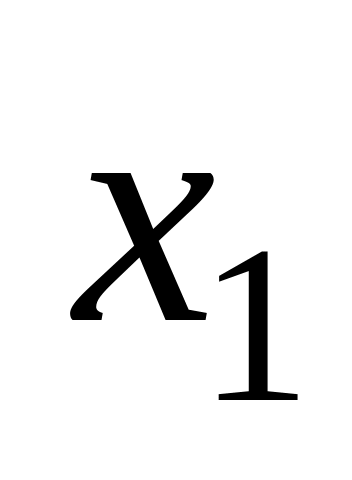 та
та
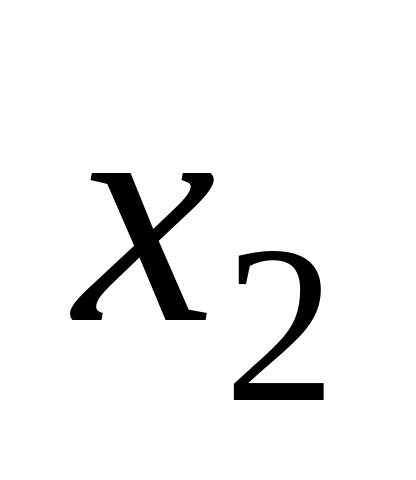 ,
причому
,
причому
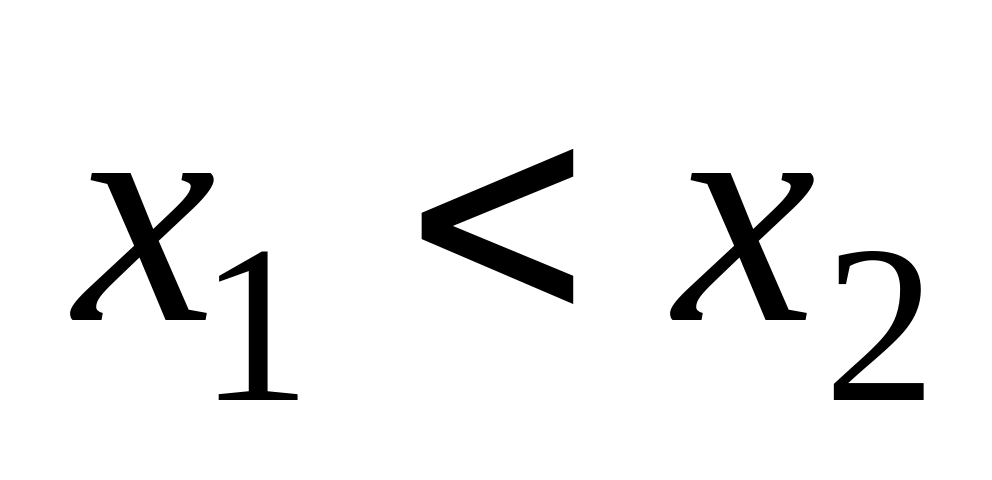 .
Відома ймовірність
.
Відома ймовірність
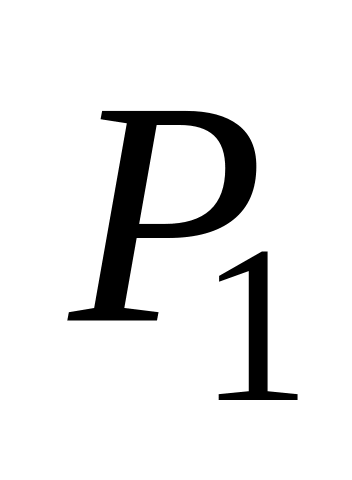 можливого значення
,
математичне сподівання
можливого значення
,
математичне сподівання
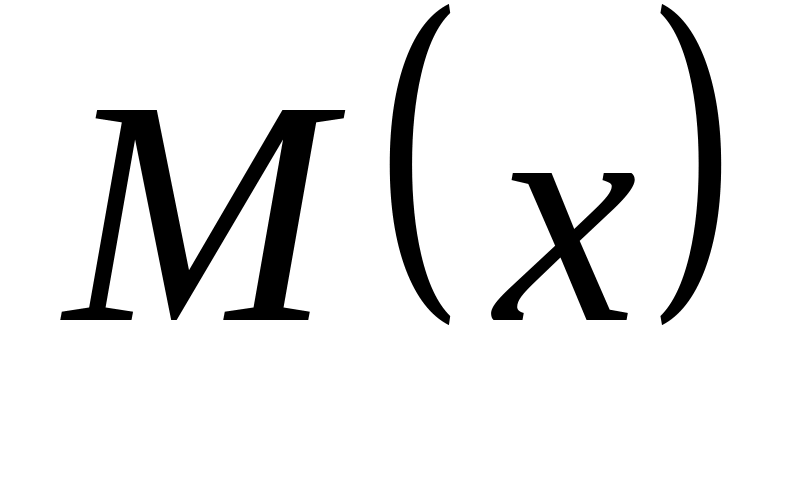 та дисперсія
та дисперсія
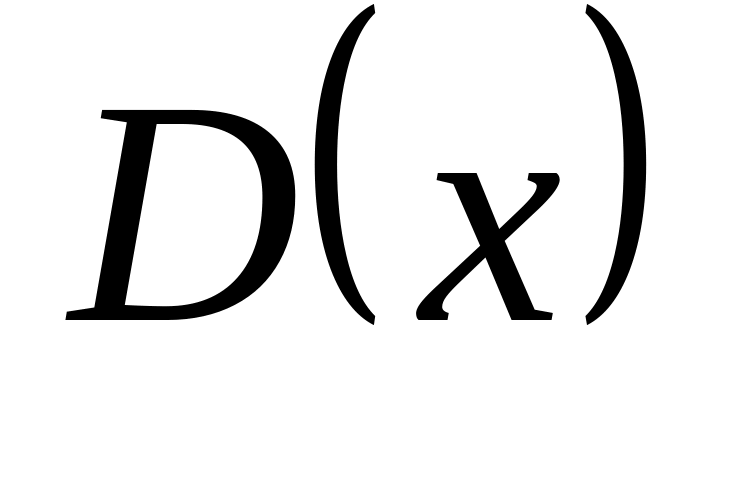 .
Знайти закон розподілу цієї випадкової
величини:
.
Знайти закон розподілу цієї випадкової
величини:
Випадкова величина задана інтегральною функцією розподілу
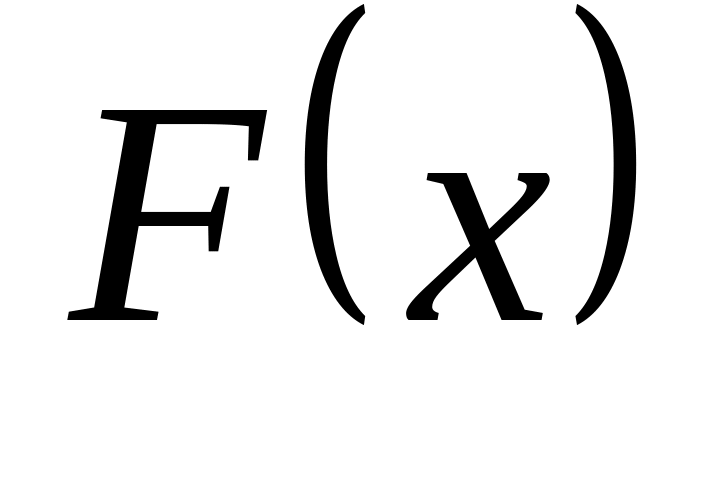 .
Треба: а) знайти диференціальну
функцію
.
Треба: а) знайти диференціальну
функцію
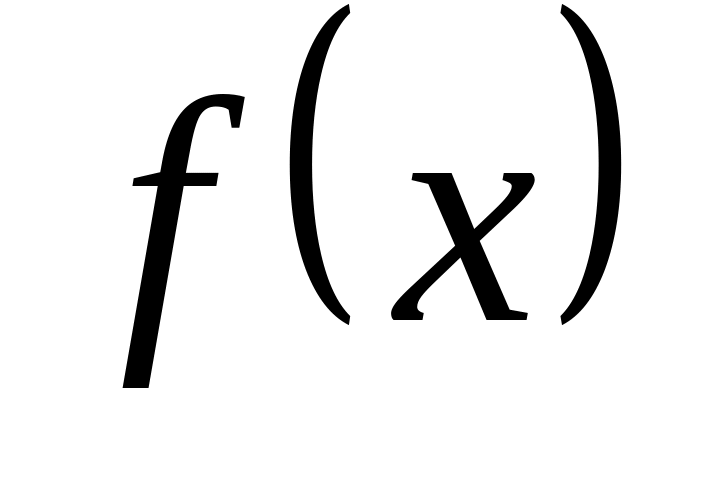 (щільність ймовірності); б) математичне
сподівання та дисперсію; в) побудувати
графіки диференціальної та інтегральної
функцій.
(щільність ймовірності); б) математичне
сподівання та дисперсію; в) побудувати
графіки диференціальної та інтегральної
функцій.
Дискретна випадкова величина задана трьома значеннями , ,
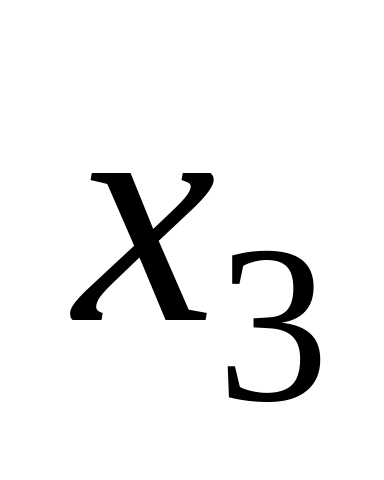 з відповідними ймовірностями
з відповідними ймовірностями
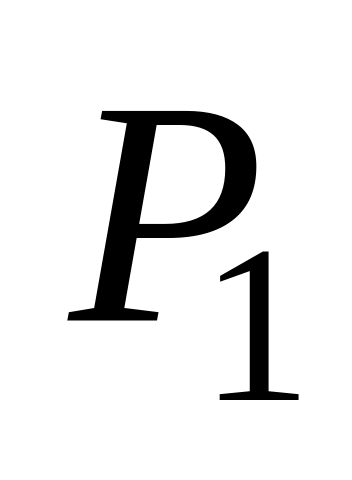 ,
,
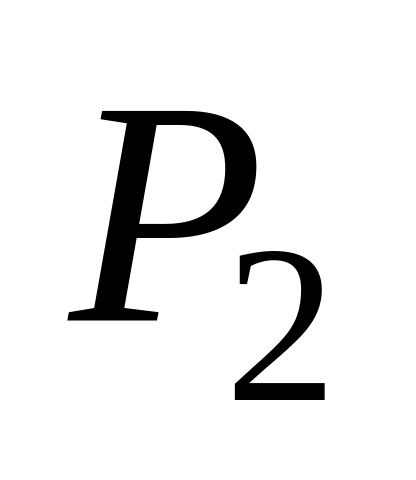 ,
,
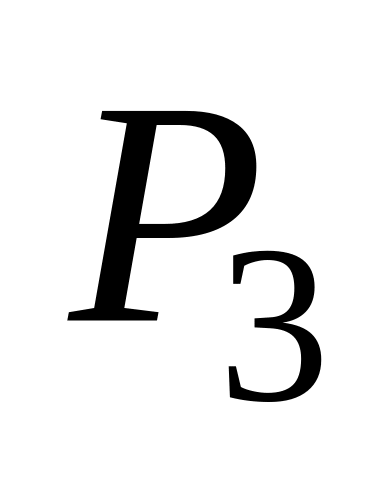 .
Знайти початкові і центральні моменти
розподілу 1-го, 2-го, 3-го і 4-го порядку:
.
Знайти початкові і центральні моменти
розподілу 1-го, 2-го, 3-го і 4-го порядку:
Випадкова величина задана диференціальною функцією розподілу
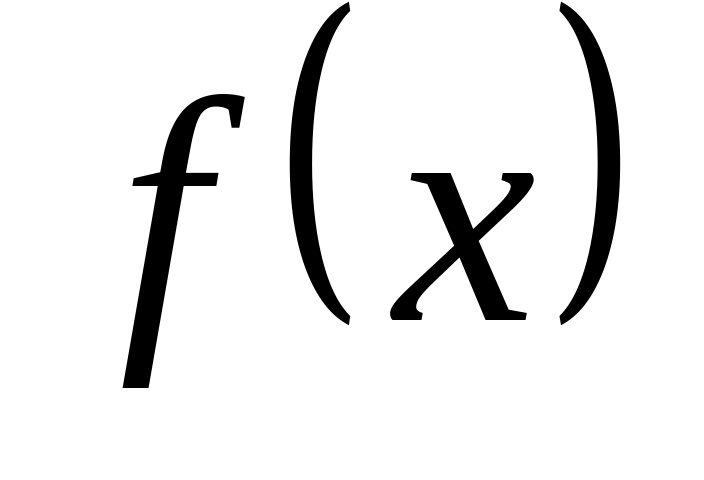 на інтервалі
на інтервалі
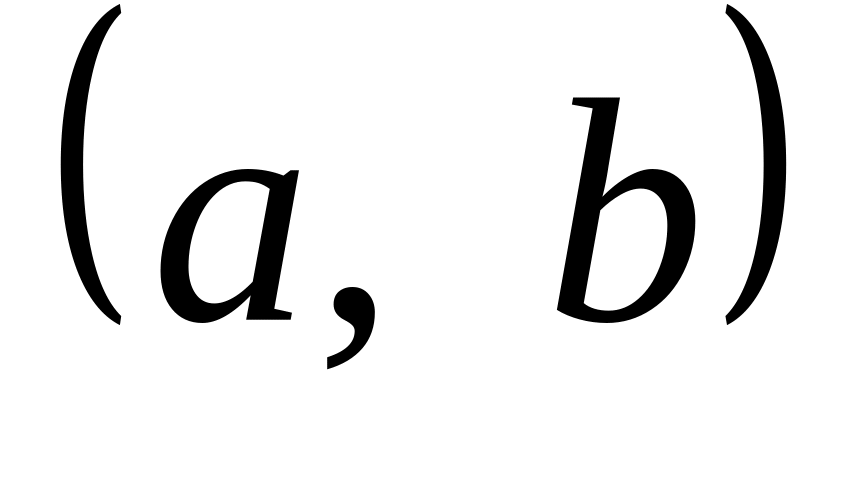 ,
поза цим інтервалом
,
поза цим інтервалом
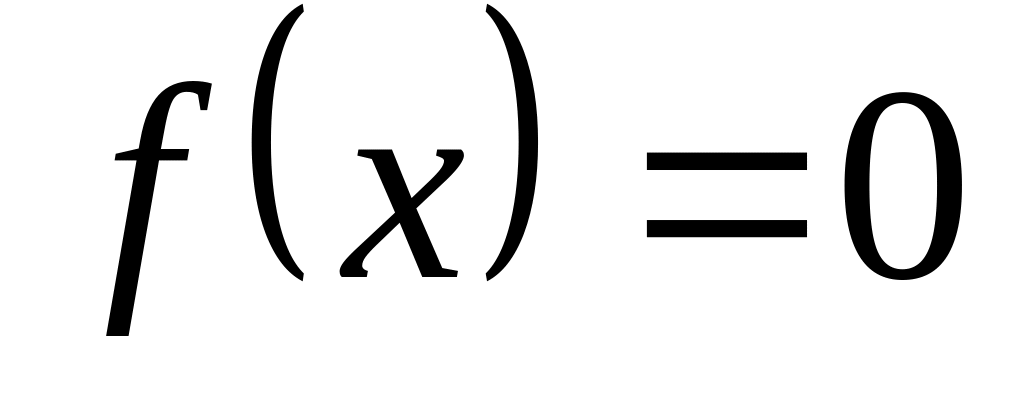 .
Знайти початкові та центральні моменти
першого, другого і третього порядків,
якщо:
.
Знайти початкові та центральні моменти
першого, другого і третього порядків,
якщо:
Відомі математичне сподівання і середнє квадратичне відхилення нормально розподіленої випадкової величини . Знайти ймовірність попадання цієї величини в заданий інтервал
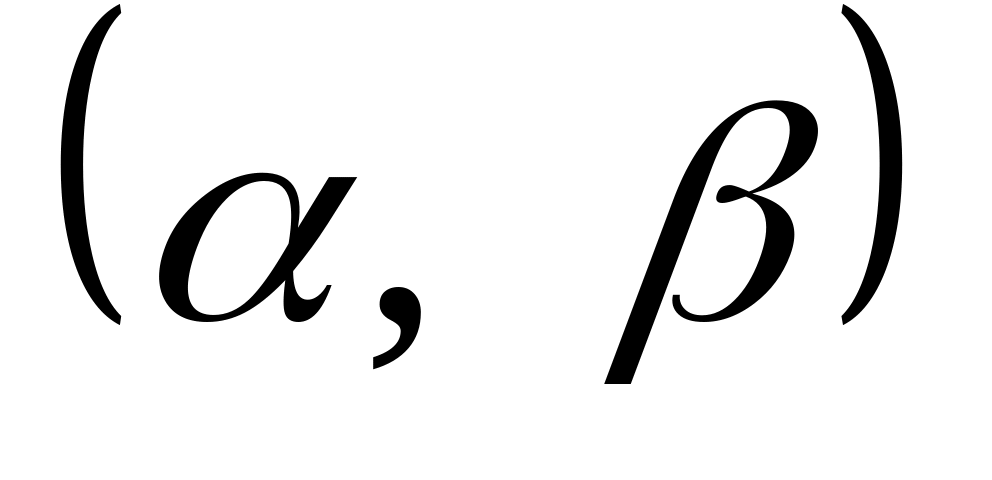 :
: