6.2 Общая схема проведения расчетов
Для проведения расчетов необходимо составить карту проведения экспериментов (табл.6.2), которая является расширенной формой матрицы планирования экспериментов, и куда заносятся результаты поставленных опытов и рассчитанные значения некоторых статистических показателей.
1. Рассчитывают построчные средние.
,
где n - общее число экспериментов;
m - число повторных опытов (серий).
Таблица 6.2
-
Пример карты проведения экспериментов для двух переменных.
?
опыта
Входы
Выходы
Построчные средние
Построчные
дисперсии
X1
X2
X1X2
y1
...
ym
1
-1
-1
+1
y11
...
y1m
2
+1
-1
-1
y21
...
y2m
3
-1
+1
-1
y31
...
y3m
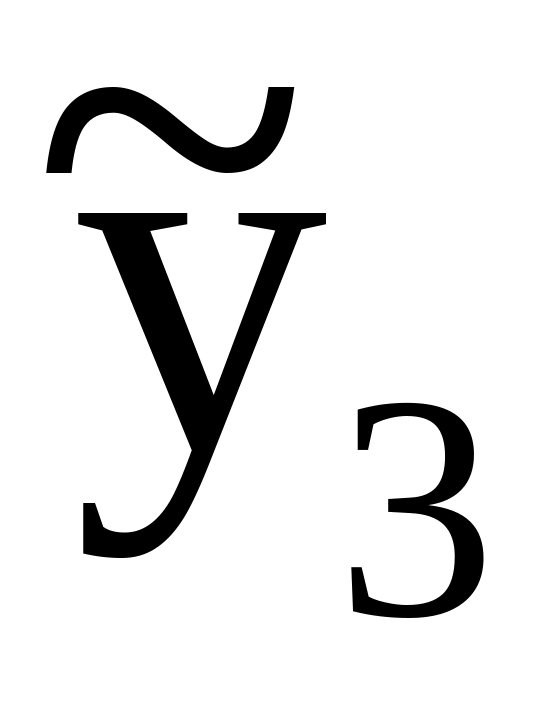
4
+1
+1
+1
y41
...
y4m
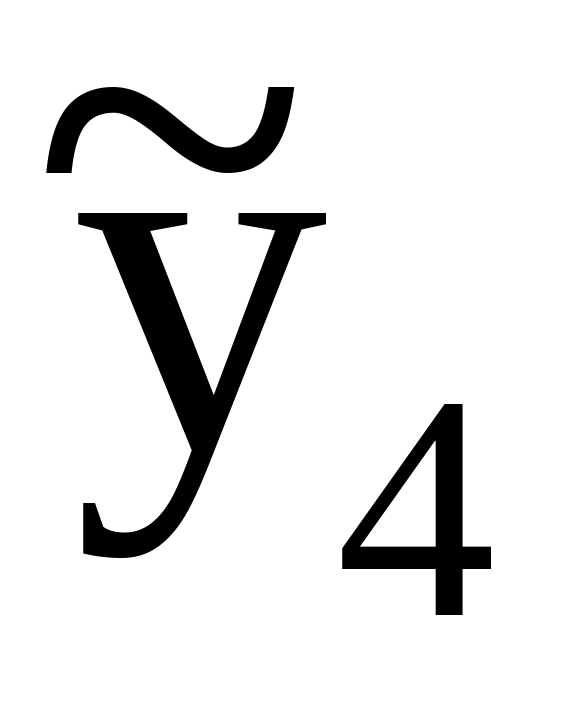
2. Определяются построчные дисперсии (дисперсии воспроизводимости). Проверка воспроизводимости осуществляется с использованием критерия Кохрена (Кочрена). Проверка воспроизводимости является важнейшей предпосылкой, лишь при выполнении которой результатам опытов и полученным на их основе закономерностям можно доверять.
2.1. Определяются построчные дисперсии:
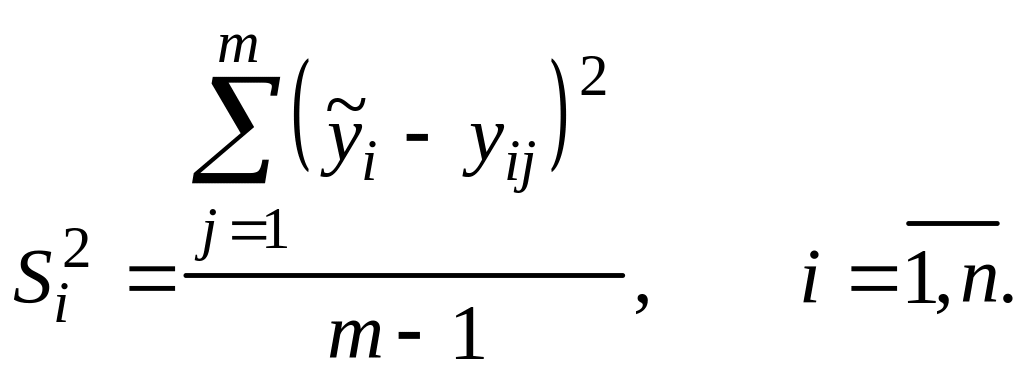
2.2.Определяется
сумма построчных дисперсий:
2.3. Определяется
максимальная из построчных дисперсий:
2.4. Проверяется
воспроизводимость опытов по критерию
Кохрена:
2.5. Определяется табличное значение критерия Кохрена Hтабл, выбираемое в зависимости от числа опытов n, числа повторных опытов (число серий) m, и уровня значимости p (надежности). Опыты считаются равноточными, если: H < Hтабл. В случае неравноточности опытов необходимо увеличить число повторных экспериментов или повысить их точность.
3. Определяются коэффициенты уравнения регрессии.
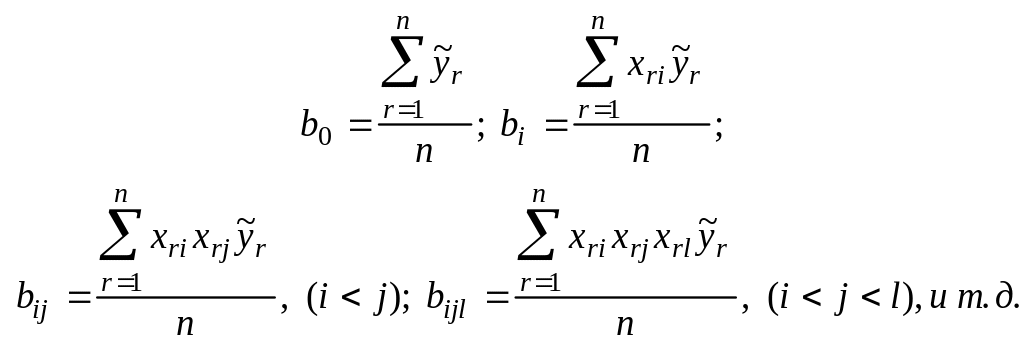
Индекс любого
коэффициента
показывает компонент уравнения регрессии,
множителем которого он является.
В формулах
суммирования у кодированной переменной
первый
индекс r - есть
номер опыта (строки) в карте проведения
эксперимента, второй индекс i
- номер кодированной переменной.
Например,
-
значение кодированной переменной
в третьем опыте, равное, например, (+1)
(см. табл.5.2).
Коэффициент b0 по физическому смыслу соответствует опыту с поддержанием всех варьируемых факторов на средних (нулевых) уровнях.
4. Определяется значимость коэффициентов регрессии.
Для этого требуется рассчитать следующие показатели.
4.1. Дисперсия эксперимента:
;
4.2. Усредненная
дисперсия эксперимента с учетом
повторности опытов:
4.3. Определяют дисперсию и среднюю квадратичную ошибку коэффициентов регрессии:
4.4. Определяется область значимости значений коэффициентов регрессии: b=t*b , где t - табличное значение критерия Стьюдента, выбираемое в зависимости от числа степеней свободы: f2=n*( m-1 ) и выбранного уровня значимости (обычно 0.05).
4.5 Определяются значимые и незначимые коэффициенты в уравнении регрессии.
Коэффициент
- значим, если его абсолютная величина
больше параметра b,
определяющего границы области значимости
коэффициентов:
,
то есть коэффициент должен быть больше
ошибки его определения, взятой с
определенным запасом.
После того как выявлены все значимые и незначимые коэффициенты уравнения регрессии, можно выписать в явном виде собственно уравнение регрессии. Для этого удаляются все незначимые компоненты уравнения регрессии, определяя тем самым уравнение регрессии в кодированных переменных с полученным численными значениями значимых коэффициентов. При необходимости перехода от кодированных переменных к натуральным, следует подставить в полученное уравнение соотношения связи между этими переменными.