3.5 Управление модельным временем

3.5.1 Виды представления времени в модели

При разработке ИМ необходимо соотносить между собой три представления времени:

- реальное время, в котором происходит функционирование системы (например, работа лаборатории в течение недели);

- модельное (или системное) время, в масштабах которого организуется работа модели;

- компьютерное время, то есть затраты времени на проведение имитации.

С помощью механизма модельного времени решаются следующие задачи:

• отображается переход моделируемой системы из одного состояния в другое;

• производится синхронизация работы компонент модели;

• изменяется масштаб времени «жизни» исследуемой системы;

• производится управление ходом модельного эксперимента;

• моделируется квазипараллельная реализация событий в модели.

Выбор метода реализации механизма модельного времени зависит от назначения модели, ее сложности, характера исследуемых процессов, требуемой точности и т.д.

Наиболее известны два метода учета модельного времени: с постоянным шагом и по особым состояниям.

3.5.2 Изменение времени с постоянным шагом

Для данного метода отсчет системного времени ведется через фиксированные, выбранные исследователем интервалы времени t. События в модели считаются наступившими в момент окончания этого интервала. Погрешность в измерении временных характеристик зависит от величины шага моделирования t.

Метод с постоянным шагом следует использовать тогда, когда:

• события появляются регулярно, их распределение по времени – равномерно;

• число событий велико и моменты их появления близки;

• невозможно заранее определить моменты появления событий.

Р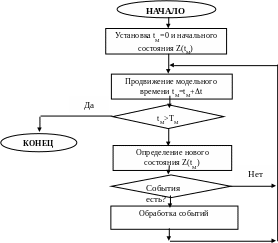 ис.3.3 Моделирование с постоянным шагом

В общем виде алгоритм моделирования с постоянным шагом приведен на рис. 3.3 (t_М – текущее значение модельного времени, T_M – заданный интервал моделирования).

Пример. Пусть событие состоит в том, что летящий самолет пересекает рубеж, расстояние до которого R. Если объект движется равномерно, по его пройденный путь S=S+V*t. Событие наступает, если S>R, а момент наступления события t=n*t, где n –номер шага моделирования, на котором условие стало истинным.

При моделировании с постоянным шагом результат моделирования напрямую зависит от величины шага. Если шаг будет очень большим, то результат, скорее всего, будет неверным: момент окончания очередного шага очень редко будет совпадать с реальным моментом пересечения самолетом заданного рубежа.

Влияние величины шага на точность моделирования показано на рис.3.4.

В ыбор величины шага моделирования является важным и непростым делом. Универсальной методики не существует, но можно использовать один из следующих подходов:

1) принимать величину шага равной средней интенсивности возникновения различных событий;

2) выбирать величину t равной среднему интервалу между наиболее частыми (или важными) событиями.

3.5.3 Моделирование по особым состояниям

При таком подходе системное время изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события. В этом случае события обрабатываются в порядке их наступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности.

Для реализации моделирования по особым состояниям требуется разработка специальной процедуры планирования событий (так называемого календаря событий).

Если известен закон распределения интервалов между событиями, то такое прогнозирование труда не составляет: достаточно к текущему значению модельного времени добавить величину интервала, полученную с помощью соответствующего датчика.

Пусть, например, за летящим самолетом наблюдает диспетчер. Он вводит информацию о нем, причем интервалы между вводом соседних сообщений являются случайной величиной, распределенной по нормальному закону с заданными параметрами (рис.3.5).

Рис.3.5 Пример возникновения случайных событий

Если же момент наступления события определяется некоторыми логическими условиями, то необходимо сформулировать эти условия и проверять их для каждого последующего шага моделирования. Сложность в реализации механизма времени по особым состояниям связана, в первую очередь, с корректным описанием таких условий. Трудности еще более возрастают, если в системе фигурируют несколько типов взаимосвязанных событий.

Моделирование по особым состояниям (событиям) целесообразно использовать, если:

• события распределяются по времени неравномерно или интервалы между ними велики;

• предъявляются повышенные требования к точности определения взаимного положения событий на оси времени;

• необходимо учитывать наличие одновременных событий.

Схема алгоритма моделирования по особым состояниям приведена на рис. 3.6.

Вернемся к примеру с летящим самолетом. Дополним его условием: необходимо подсчитать число сообщений, которые успеет ввести диспетчер в течение заданного интервала времени моделирования.

Что здесь понимать под особым состоянием? На практике вместо состояний рассматривают события, определяющие смену состояний. Для этого примера – событие это ввод очередного сообщения. Если интервалы между сообщениями подчиняются нормальному закону с параметрами M и S, то очередное i-ое значение модельного времени определяется как t_M(i)=t_M(i-1)+norm(M,S), где norm(M,S) – генератор случайных чисел, распределенных по нормальному закону.

В ыводы:

выбор механизма изменения модельного времени определяет технологию реализации имитационной модели;

на выбор метода моделирования влияет целый ряд факторов, но определяющим является тип моделируемой системы: для дискретных систем, события в которых распределены во времени неравномерно, более удобным является изменение модельного времени по особым состояниям;

если в модели должны быть представлены компоненты реальной системы, работа которых измеряется в разных единицах времени, то они должны быть предварительно приведены к единому масштабу.