7. Матричное моделирование в анализе межотраслевых связей

Межотраслевой баланс производства и распределения продукции является результатом развития балансового метода анализа и планирования народного хозяйства. Межотраслевой баланс позволяет проверить сбалансированность народно-хозяйственного плана, соблюдение установленных пропорций развития различных отраслей народного хозяйства, а также межотраслевых и внутриотраслевых пропорций.

Структуру межотраслевого баланса можно представить в виде табл. (матрицы) 7.1.

Строки табл. 7.1. показывают распределение выпуска каждого вида продукции. Каждая строка характеризуется следующим балансом:

Выпуск данного вида продукции

=

Промежуточный спрос

+

Конечный спрос,

что математически может быть записано как

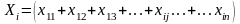(7.1)

Промежуточный спрос есть часть общего спроса, представляющая собой закупки данного вида продукции отраслями 1, 2, 3, и т. д. в качестве исходных материалов, то есть в качестве промежуточных продуктов. Напротив конечный спрос есть часть спроса, представляющая закупки конечных продуктов – потребительских или инвестиционных.

Таблица 7.1

Таблица межотраслевого баланса

Отрасли Покупатели сектора спроса Отрасли Продавцы сектора предло- жение

1

2

3

... j ...

n

Конечный спрос (продукция) Потребление, инвестиции, экспорт, импорт (со знаком «-», и т. д.)

Валовая продукция

1. 2. 3. ... i ... n

x11 x21 x31 . . . . xn1

x12 x22 x32 . . . . xn2

x13 x23 x33 . . . . xn3

... ... ... . . . . ...

x1n x2n x3n . . . . xnn

y1 y2 y3 . . . . yn

x1 x2 x3 . . . . xn

Добавленная стоимость

Оплата труда Чистый доход (прибыль, амортизац. отчисл., налоги и т.д.)

k1 l1

k2 l2

k3 l3

... ...

kn ln

Валовая продукция

x1

x2

x3

...

xn

Столбцы таблицы показывают структуру затрат, или структуру используемых ресурсов, необходимых для каждой отрасли. Для столбцов устанавливается следующий баланс:

Расходы отрасли

=

Промежуточные затраты

+

Добавленная стоимость,

что в математической записи выглядит как

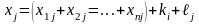. (7.2)

Промежуточные затраты представляют собой исходные материалы, закупленные отраслью у секторов 1, 2, 3, и т. д. Добавленная стоимость есть факторные затраты отрасли, т.е. вновь созданная стоимость, распадающаяся на доход работающих по найму (заработную плату) и предпринимательской (чистый) доход (прибыль).

Для строк и столбцов таблицы межотраслевого баланса имеют место следующие тождества:

Выпуск отрасли = Расходы отрасли

Общая сумма конечного спроса = Общая сумма добавленной стоимости,

которые математически записывается так

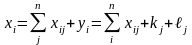, (7.3)

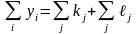. (7.4)

Для доказательства соотношения (7.4) достаточно сложить почленно правое и левое части уравнений (7.2), (7.1), образующих системы. В результате получим два равенства

,

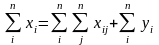
а отсюда следует выражение (7.4).

Таблица межотраслевого баланса позволяет изучать структуру потоков ресурсов, однако, для понимания функционирования экономики, в частности эффекта распространения (мультипликации) необходим еще один шаг, заключающийся в построении таблиц коэффициентов прямых затрат и коэффициентов полных затрат.

Коэффициент прямых затрат определяется как объем ресурса i, необходимый для производства единицы продукции j, т. е.

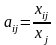(7.5)

После подстановки 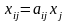, получаем

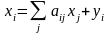(7.6)

Система уравнений, составленная из уравнений вида (7.6), позволяет сформулировать как минимум три типа задач межотраслевого баланса:

1) Известны коэффициенты прямых материальных затрат 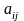и объемы конечного продукта всех отраслей (или спроса); найти объемы производства (валовой продукции) 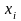каждой отрасли;

2) При заданных объемах валовой продукции (объемах производства) всех отраслей и известных коэффициентах прямых материальных затрат, найти объемы конечной продукции всех отраслей.

3) Известны коэффициенты прямых материальных затрат , заданы объемы валовой продукции части отраслей и объемы конечной продукции остальных отраслей; найти объемы чистой продукции первой и валовую продукцию вторых отраслей.

Решение системы уравнений межотраслевого баланса в матричной форме возможно при использовании матрицы полных материальных затрат, которая может быть представлена в виде

[E_n-A]^-1 = B =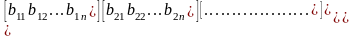 . (7.7)

Матрица B называется обратной матрицей Леонтьева или, по аналогии с кейнсианской концепцией мультипликатора, матричным мультипликатором, или мультипликатором Леонтьева. Экономический смысл ее элементов 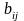заключается в следующем: коэффициент показывает потребность в валовом выпуске продукции отрасли для производства единицы конечной продукции отрасли .

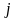Введенные раньше коэффициенты прямых затрат характеризуют непосредственно затраты продукции i отрасли на производство единицы продукции j отрасли. Но кроме прямых затрат на производство продукции j отрасли осуществляются и так называемые косвенные затраты которые учитываются в коэффициенте смысл их будет ясен, если рассмотреть такой пример.

Пусть одним из видов продукции пищевой промышленности является хлеб. Для производства хлеба необходимы мука, электроэнергия и многое другое, что непосредственно используется при выпечке хлеба. Это прямые затраты продукции при выпечке хлеба. Но при производстве муки необходимы затраты другой продукции – зерна, электроэнергии и др. Эти затраты – прямые при производстве муки и косвенные при производстве хлеба, причем их называют косвенными затратами первого порядка. В свою очередь, для производства зерна необходимы семена, машины и др. Это прямые затраты при производстве зерна, но косвенные при производстве муки (причем косвенные затраты первого порядка) и также косвенные при производстве хлеба (их называют косвенными затратами второго порядка) (рис. 7.9).

Рис. 7.9. Схематическое изображение потребности в ресурсах при производстве хлеба

Приведенную схему косвенных затрат при производстве хлеба можно продолжить и дальше, причем практически она продолжается неограниченно.

Таким образом, в сущности есть мультипликатор, показывающий эффект распространения спроса, первоначальным источником которого является спрос на конечную продукцию. В практических расчетах косвенными затратами высоких порядков можно пренебречь вследствие их малости, поэтому значения полных затрат получаются приближенными.

Косвенные затраты вычисляются следующим образом.

Пусть имеется матрица коэффициентов прямых затрат в натуральном или стоимостном выражении

A = (a_ij)_n×n (7.8)

Для производства единицы продукции отрасли j необходимо затра­тить набор продуктов а^j = (a_1j, a_2j,.., a_nj), который формально описыва­ется j-м столбцом матрицы А. Но для производства этого набора необ­ходимо непосредственно затратить набор продуктов, который мы обозначим через а^j(1).

а^j(1)= Aa_j (7.9)

Элементы вектора затрат а^j(1) называются коэффициентами косвен­ных затрат первого порядка соответствующих продуктов на производ­ство единицы продукта j.

Матрица A⁽¹⁾, составленная из столбцов а^j(1)j=1,2,..п, называется матрицей косвенных затрат первого порядка. Очевидно, что

A⁽¹⁾ = AхA=A². (7.10)

Косвенными затратами второго порядка называются прямые затраты, необходимые для обеспечения косвенных затрат первого порядка, т. е.

а^j(2)=Aа^j(1) ,

или в матричной форме

A⁽²⁾ = AхA⁽¹⁾ = A³ (7.11)

где A⁽²⁾ — матрица коэффициентов косвенных затрат второго порядка.

Продолжая по аналогии, назовем косвенными затратами порядка т прямые затраты на обеспечение косвенных затрат порядка (т - 1). Очевидно, что матрицу коэффициентов косвенных затрат т-го поряд­ка получим, умножив матрицу А на матрицу А^m-1

A^(m)=А×A^(m-1)=A^m+1 (7.12)

Для вычисления матрицы полных затрат используются итерационный метод. Идея этого метода заключается в следующем. Если предположить, что матрицы E_n и A − есть матрицы первого порядка, содержащие по одному элементу, то матрицей обратной матрице [E_n-A] = [1-a] будет матрица вида

[E_n-A]^-1 = .

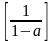Элемент этой матрицы – число 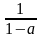можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии, первый член которой равен 1, а знаменатель прогрессии равен «a»:

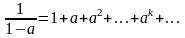(7.13)

Аналогично вычисляются приближенно элементы матрицы [E_n-A]^-1n порядка, то есть с учетом (7.7) и (7.13)

B = [E_n-A]^-1 = E_n + A+A² + A³ +A⁴ …+A^m +… (7.14)

Правая часть выражения (7.14.) есть сумма неограниченного числа матриц. Чтобы вычислить приближенно элементы матрицы полных затрат, достаточно взять сумму первых k членов ряда (7.14.).

Матрицы A², A³ и т. д. вычисляются последовательно, учитывая, что

A^m+1 = A^mA. Отсюда и название метода – метод последовательных приближений, или итерационный метод.

Определим теперь полные затраты как сумму прямых и косвенных затрат всех порядков.

B = E_n + A+A⁽¹⁾ + A⁽²⁾ + A⁽³⁾ +…+A^(m-1) +… (7.15)

Выражение (7.14) легко преобразуется в (7.15) с учетом (7.12).

Строго говоря, полные материальные затраты, определенные выше, не являются в действительности полными, т. е. не учитывают всех ма­териальных затрат. Это происходит в основном по двум причинам. Bо-первых, элементы матрицы А не учитывают прямых материальных затрат на восстановление основных фондов. Во-вторых, при расчете не учитываются косвенные материальные затраты, необходимые для воспроизводства рабочей силы.

Коэффициенты прямых и полных материальных затрат имеют важ­ное значение для характеристики структуры технико-экономических связей и для анализа эффективности общественного производства со стороны затрат овеществленного труда. С этой точки зрения и матри­ца А, и матрица B несут одну и ту же информацию, но в разной форме. Существенное отличие коэффициентов полных затрат от коэффици­ентов прямых затрат состоит в том, что они являются не отраслевыми, а народнохозяйственными показателями и формируются с учетом тех­нологических связей между отраслями.

Задачи для самостоятельного решения

Задача 7.1

Пусть в некотором производстве используется четыре вида продуктов: A, B, C, D, причем для производства каждого продукта используется только три из имеющихся четырех продуктов, а в производстве каждого из этих продуктов не участвует. Коэффициенты прямых затрат приведены в таблице для каждого варианта. Используя данные таблиц, составленным по вариантам выполнить следующие задания.

Задание 1. Вычислить коэффициенты полных материальных затрат продукта В на производство единицы продукта А, учитывая при этом косвенные затраты только первых двух порядков.

Задание 2. Вычислить коэффициенты полных затрат: а) продукта А; б) продукта С; в) продукта D на производство единицы продукта А, учитывая при этом косвенные затраты только первых двух порядков.

Вариант 1(А)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.1	0.3	0.4
B	0.2	0	0.4	0.1
C	0.5	0.1	0	0.3
D	0.1	0.6	0.2	0

Вариант 2 (Б)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.2	0.3	0.3
B	0.1	0	0.5	0.1
C	0.3	0.1	0	0.3
D	0.2	0.6	0.1	0

Вариант 3 (В)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.5	0.3	0.1
B	0.3	0	0.4	0.1
C	0.5	0.1	0	0.3
D	0.1	0.3	0.2	0

Вариант 4 (Г)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.4	0.2	0.3
B	0.1	0	0.4	0.4
C	0.5	0.1	0	0.2
D	0.1	0.3	0.2	0

Варианты 5 (Д)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.6	0.1	0.1
B	0.2	0	0.4	0.1
C	0.5	0.2	0	0.2
D	0.1	0.1	0.4	0

Варианты 6 (Е, Ё)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.4	0.1	0.1
B	0.2	0	0.3	0.1
C	0.5	0.2	0	0.1
D	0.1	0.1	0.4	0

Вариант 7-8 (Ж, З)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.4	0.1	0.2
B	0.2	0	0.4	0.1
C	0.4	0.3	0	0.2
D	0.1	0.1	0.4	0

Вариант 9 (И)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.1	0.3	0.4
B	0.2	0	0.4	0.1
C	0.5	0.1	0	0.3
D	0.1	0.6	0.2	0

Вариант 10 (К)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.6	0.1	0.1
B	0.4	0	0.4	0.1
C	0.55	0.1	0	0.25
D	0.1	0.1	0.4	0

Вариант 11 (Л)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.35	0.15	0.1
B	0.15	0	0.3	0.1
C	0.2	0.08	0	0.25
D	0.1	0.1	0.4	0

Вариант 12-13 (М, Н)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.2	0.6	0.4
B	0.18	0	0.4	0.1
C	0.13	0.09	0	0.3
D	0.1	0.6	0.2	0

Вариант 14-15 (О, П)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.1	0.3	0.4
B	0.2	0	0.5	0.2
C	0.5	0.16	0	0.3
D	0.1	0.2	0.05	0

Вариант 16-17 (Р, С)

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0,4	0.2	0.2
B	0.2	0	0,2	0.3
C	0.5	0.13	0	0,07
D	0.3	0.6	0.2	0

Вариант 18-19 (Т, У).

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.4	0.2	0.3
B	0,36	0	0.4	0.42
C	0.5	0,12	0	0.2
D	0.19	0.04	0,1	0

Вариант 20-21 (Ф, Х).

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.2	0.24	0.36
B	0.05	0	0. 7	0.4
C	0.19	0.04	0	0.19
D	0.1	0.3	0.2	0

Вариант 22-26 (Ц, Ч, Ш, Щ, Э, Ю, Я).

Затрачиваемый продукт	Выпускаемый продукт
	A	B	C	D
A	0	0.4	0.12	0.3
B	0.1	0	0.2	0.25
C	0.5	0.5	0,	0.07
D	0.15	0.19	0.4	0,