Контрольные вопросы

1. Что такое генерация и рекомбинация, равновесные и неравновесные носители?

2. Как можно рассчитать концентрацию неравновесных носителей?

3. Закон действующих масс для равновесных и неравновесных носителей.

4. Время жизни носителей заряда. Как его рассчитать при малом и большом уровне возбуждения?

5. Как определить время жизни носителей заряда при нескольких механизмах рекомбинации?

6. Перечислите и кратко охарактеризуйте основные типы рекомбинации.

7. Что такое центры захвата (центры прилипания) и рекомбинационные ловушки?

8. Поясните физику процесса фотопроводимости.

9. Какими параметрами характеризуется стационарная фотопроводимость?

10. Частотный метод измерения времени жизни.

11. Принцип действия экспериментальной установки.

12. Охарактеризуйте возможные погрешности частотного метода измерения.

Литература

1 Спиридонов О.П. Физические основы твердотельной электроники.-М.: Высшая школа, 2008.-190с.

2 Шалимова К. В. Физика полупроводников. – М.: Энергоатомиздат, 1985.

3. Павлов Л. П. Методы измерения параметров полупроводниковых материалов. – М.: Высшая школа, 1987.

Лабораторная работа № 4 Исследование термоэлектронной эмиссии металлов

Цель работы: освоение экспериментальной методики исследова­ния термоэлектронной эмиссии металлов; проверка правильности экспоненциального закона термоэмиссии; определение работы выхода и термоэлектронной постоянной методом прямой Ричардсона.

Теоретическое введение

Потенциальный барьер на границе металл-вакуум. В модели металла Зоммерфельда свободные электроны находятся в потенциальном “ящике” с плоским дном и высотой U₀ . Свободные электроны заполняют этот ящик до уровня Ферми . Чтобы покинуть металл, электрон должен совершить работу по преодолению потенциального барьера, которую называют работой выхода.

Введённое таким образом понятие работы выхода не является определённым, поскольку не указывает на начальный отсчёт этой величины. Так как в металле электроны даже при Т=0 К обладают некоторой энергией, максимальное значение которой равно энергии Ферми, то целесообразно эту энергию взять за начало отсчёта. Термодинамической работой выхода называют работу по переводу электрона с уровня Ферми на уровень вакуума

(1)

Более полным является следующее определение: работа выхода электрона Ф определяется минимальной энергией, необходимой для перемещения его с поверхности Ферми в металле при температуре, равной абсолютному нулю, в точку пространства, где поле практически равно нулю. Поскольку электрическое поле создаётся как объемными, так и поверхностными атомами, то обе составляющие работы выхода следует учитывать.

Рассмотрим более реалистичную конфигурацию потенциального барьера. При выходе электрона за пределы твёрдого тела на него действует возвращающая сила со стороны нескомпенсированного положительного заряда (рисунок 1,а). Расчет силы взаимодействия может быть проведён методом

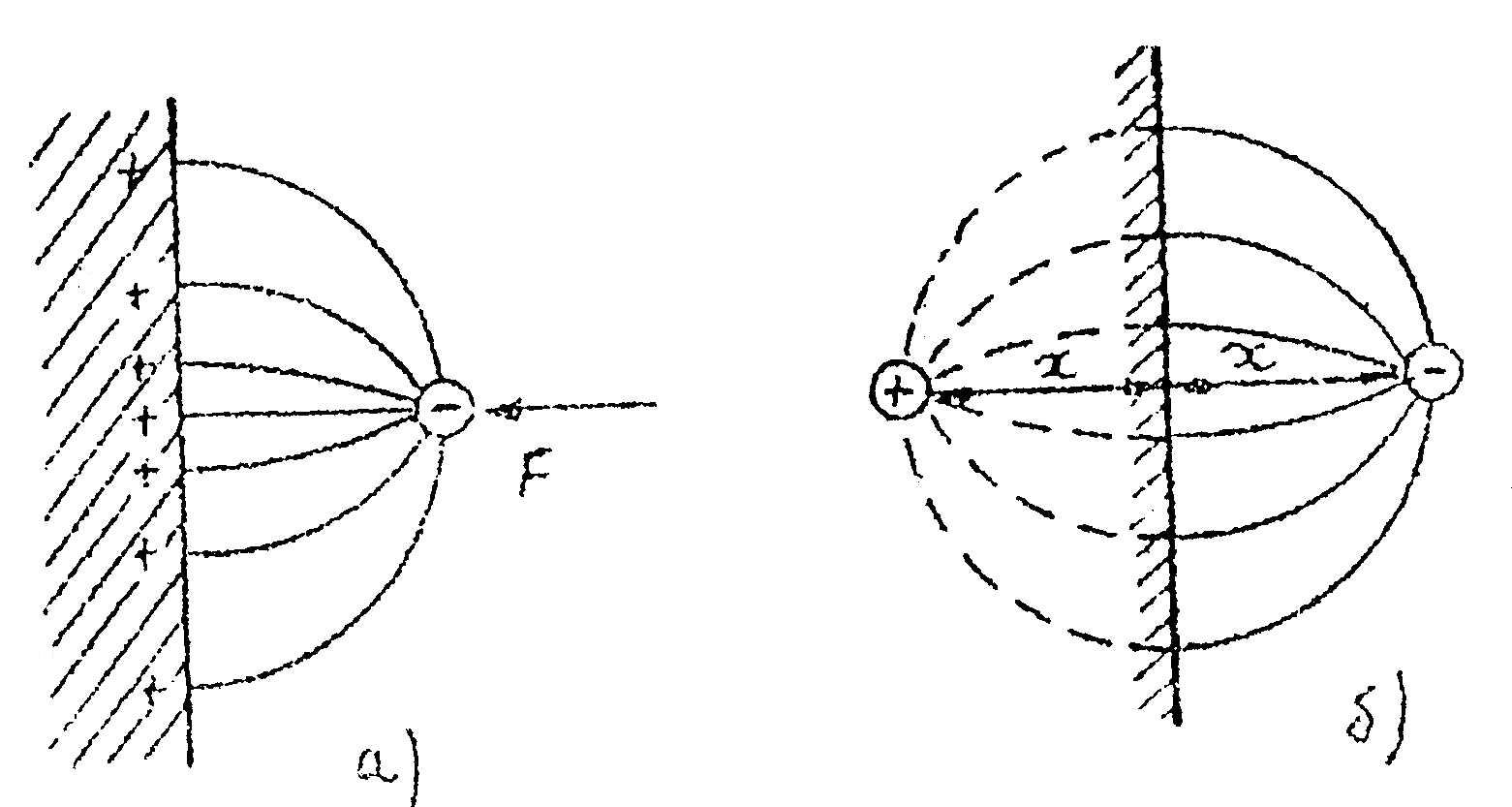
Рисунок1- К расчету формы потенциального барьера

у поверхности металла

зеркального отображения, суть которого в том, что распределённый по всей поверхности заряд заменяется точечным положительным зарядом, находящимся по другую сторону на таком же расстоянии от поверхности, что и рассматриваемый электрон ( рисунок 1,б ). Сила, действующая на электрон, в соответствии с законом Кулона

(2)

Потенциальная энергия электрона равна работе по перемещению его из данной точки на бесконечность и определяется как интеграл от силы

(3)

Полученная потенциальная энергия равна нулю при , что соответствует минимально возможной энергии свободного электрона в вакууме, и называется уровнем вакуума. Функция (3) описывает форму потенциального барьера, существующего у поверхности и препятствующего выходу электронов из металла ( рисунок 2 ).

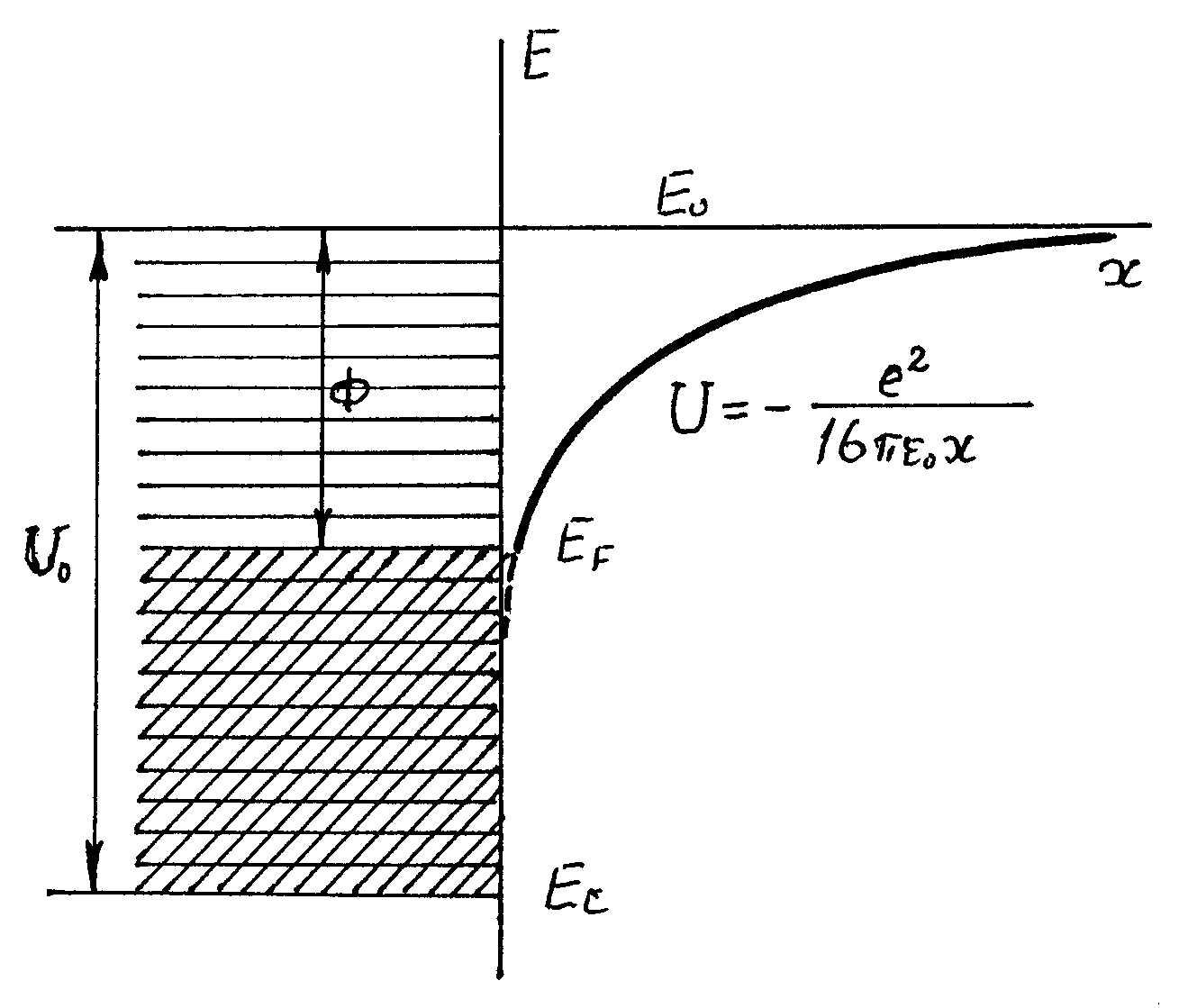
Рисунок 2 - Потенциальный барьер на границе металл-вакуум

При отсчёте потенциальной энергии электрона от дна зоны проводимости потенциальная энергия электрона в вакууме вблизи границы раздела металл – вакуум имеет вид

(4)

Соотношения (3) и .4) справедливы при x > 0,3 нм. Точная форма барьера при x < 0,3 нм зависит от конкретной поверхности металла. В традиционных теориях электронной эмиссии в приближении свободных электронов принимается, что (3) и (4) справедливы вплоть до точки x_c, когда U(x_c) = 0.

Влияние электрического поля на работу выхода. Силы зеркального отображения, существующие у поверхности металла и препятствующее выходу из него электронов, могут быть ослаблены внешним электрическим полем, если поле является ускоряющим, т.е. если его силовые линии направлены к поверхности катода. Это приводит к снижению потенциального барьера и соответственно к уменьшению работы выхода.

Для количественного анализа рассмотрим плоский металлический катод, у поверхности которого действует сила зеркального отображения и сила электрического поля . Эти силы направлены навстречу друг другу и в точке

(5)

взаимно компенсируются, что следует непосредственно из равенства этих сил. Силы кристаллической решётки препятствуют выходу электрона только до точки x_m, а при больших расстояниях поле будет ускоряющим. Потенциальная энергия будет определяться суммой энергий в поле решетки (3) и во внешнем поле (рисунок 3)

(6)

Точка х_m соответствует максимуму потенциальной энергии и определяет наибольшую высоту потенциального барьера. Из рисунка 3 видно, что снижение потенциального барьера равно

( 7)

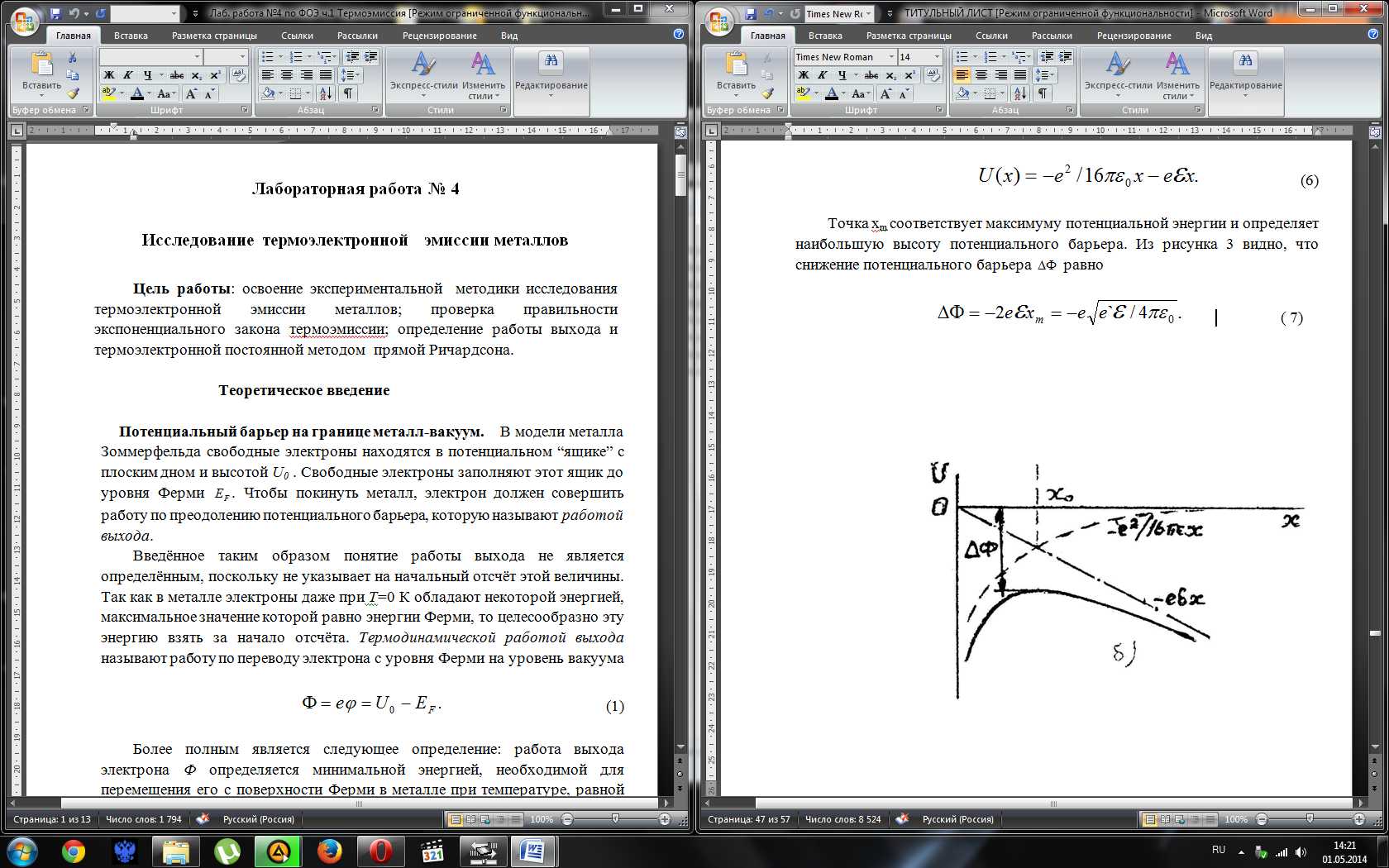
Рисунок 3 –Изменение потенциальной энергии

у поверхности металла

Такое снижение потенциального барьера при наличии ускоряющего поля называют эффектом Шоттки, а уменьшение работы выхода по (7) – шоттковским снижением работы выхода.

Сущность термоэлектронной эмиссии. Термоэлектронной эмиссией называется испускание электронов нагретыми телами. Источником энергии возбуждения электронов служит энергия тепловых колебаний решетки. У нагретых тел "хвост" фермиевской функции f_F(E) распределения электронов по энергиям заметно простирается в область, где E>E_F. Термоэмиссия из металлов оказывается возможной благодаря тому, что при температуре часть электронов в состоянии термодинамического равновесия имеет энергию, достаточную для того, чтобы покинуть металл (рисунок 4).

Основной задачей теории собственно термоэлектронной эмиссии является вычисление величины j_T - плотности максимально возможного для данной поверхности при данной температуре термоэмиссионного тока, называемого также током насыщения. Величина j_T полностью определяется температурой и свойствами металла – эмиттера.

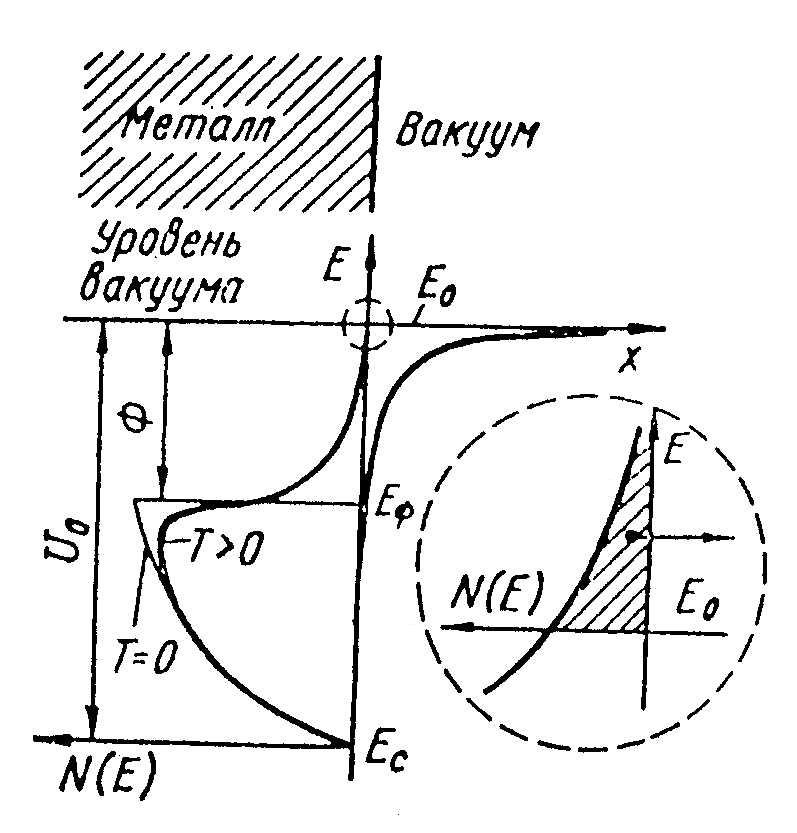
Рисунок 4 - Энергетическая диаграмма электронов

у поверхности металла

Плотность тока термоэлектронной эмиссии можно определить, зная состояние электронного газа внутри эмиттера. Для этого надо вычислить поток электронов, падающих изнутри эмиттера на его границу с вакуумом, и рассмотреть прохождение электронов через эту границу. Расчёт для модели металла как “ящика” с плоским дном, заполненного идеальным электронным газом, подчиняющимся статистике Максвелла-Больцмана приводит к уравнению

, (8)

где =120 10⁴ А/(м²К²).

Выражение (8) называют уравнением Ричардсона – Дешмана (иногда уравнением Ричардсона–Лауэ–Дэшмана или просто уравнением Ричардсона). Постоянную А₀ называют универсальной термоэмиссионной постоянной или термоэмиссионной постоянной Зоммерфельда.

При учете тонких эффектов термоэмиссионная константа должна, вообще говоря, зависеть от свойств металла и отличаться от А₀.

Для практического применения формулу Ричардсона – Дешмана (8) записывают в виде

(9)

где А – термоэмиссионная константа для данного эмиттера, которую иногда называют, чтобы отличить от А₀, ричардсоновской термоэлектронной постоянной. Экспериментальные значения констант А и j некоторых металлов приведены в таблице 1.

Таблица 1- Константы термоэлектронной эмиссии по методу прямой Ричардсона

Металл	j,В	А, 104А/м2К2	Металл	j,В	А, 104А/м2К2
Cr	4,60	48	Pt	5,32	32
Fe	4,48	26	Ta	4,19	55
Mo	4,20	55	W	4,52	60
Ni	4,61	30	LaB6	2,66	29

Расхождение в значениях А и А₀ можно объяснить неучетом ряда факторов, влияющих на процесс эмиссии: зависимость термодинамической работы выхода от температуры, отражение электронов от границы потенциального барьера и др. Учет этих факторов позволяет точнее рассчитать величину А, но отличия расчетного значения от экспериментального сохраняются.

Для определения постоянных А и φ уравнения термоэмиссии при­меняют различные методы: метод прямой Ричардсона, метод полного тока, калориметрический метод, конденсаторный метод и др.

Метод прямой Ричардсона. Разделим обе части уравнения (9) на Т² и прологарифмируем. Получим

(10)

или

(11)

Эти соотношения представляют уравнения прямой ln (j_T/T²)=f(11600/T) и

lg (j_T/T²)=f(5040/T) и носят название прямая Ричард­сона (рисунок 5).

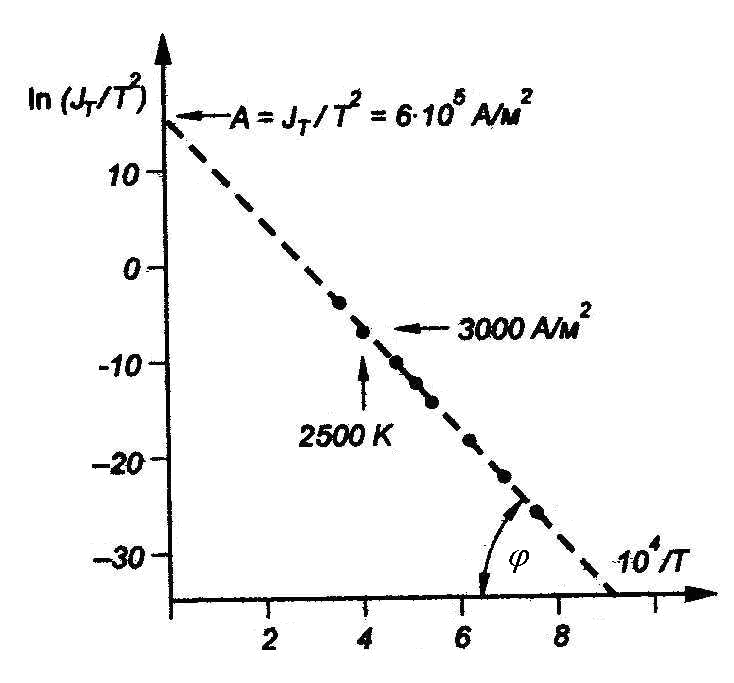
Рисунок 5 – Прямая Ричардсона

Тангенс угла наклона прямой к оси абсцисс ра­вен φ, а длина отрезка ординат, отсекаемого продолжением этой прямой, определяет величину lnA или lgA, что позволяет вычислить А. Расположение экспериментальных точек на прямой подтверждает экспоненциальный характер зависимости тока эмиссии от температуры в соответствии с уравнением (9).

На практике иногда предпочитают пользоваться уравнением пря­мой Ричардсона в виде

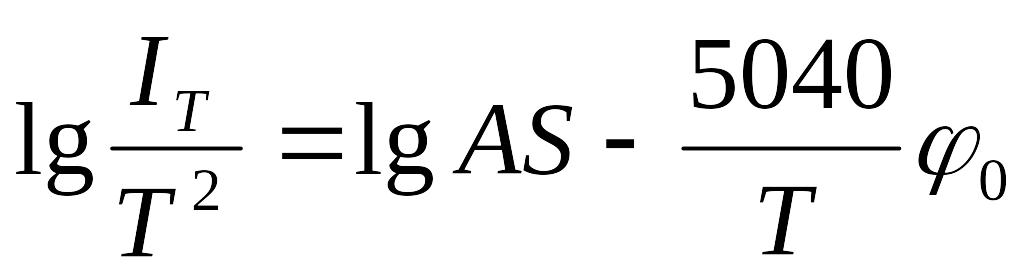, (12)

где I_T=j_TS – ток, а S - площадь эмиттера.

Достоинство метода прямых Ричардсона в том., что определяемая величина работы выхода φ₀ не искажена влиянием коэффициента прозрачности < D>. Однако она не равна истинной работе выхода катода φ и содержит ошибку ∂φ=αТ₀ , где α – температурный коэффициент работы выхода. Для металлов |α|=10^-5 В/К, так что при Т=1000 К, ∂φ=0,01 В, а значит достаточно малая. Для полупроводников |α|= (10^-4÷10^-3)В/К, так что |∂φ| (0,1-1)В, и этот метод нецелесообразно применять. Следовательно, для металлов φ₀ практически равно φ, и в уравнениях (10) и (11) вместо φ₀ записано φ.

Определение тока насыщения. При расчете постоянных А и φ требуется знать ток I_T или плотность j_T тока насыщения. Эти величины можно определить различными способами. Простой способ определения тока насыщения I_T - по перегибу вольтамперной характеристики.. Если для повышения достоверности опытов экспериментальные данные подвергаются статистической обработке, то целесообразно довести число экспериментальных точек на прямой Ричардсона до 12 – 15, т.е. снять и построить 12-15 вольт-амперных характеристик Для сокращения объема работы и времени, затрачиваемого на проведение эксперимента, поступают следующим образом. Снимают вольт-амперную характеристику при максимальном для данного эксперимента напряжении накала, что соответствует максимальной температуре катода. Строят график вольт-амперной характеристик и методом касательных находят точку перегиба. Отмечают значение напряжения V^*_a . Устанавливают напряжение на аноде V_a= V^*_а и определяют анодный ток при различных напряжениях накала от V_{н мин} до V_{н макс} .При этом полагают, что I_a(V_a= V^*_а) = I_T. В обоих способах определения тока эмиссии I_T имеется небольшая ошибка, вызванная неучетом эффекта Шоттки.

Более точное определение плотности тока насыщения j_Т возможно по графику Шоттки (рисунок 6). Прямолинейные участки графиков

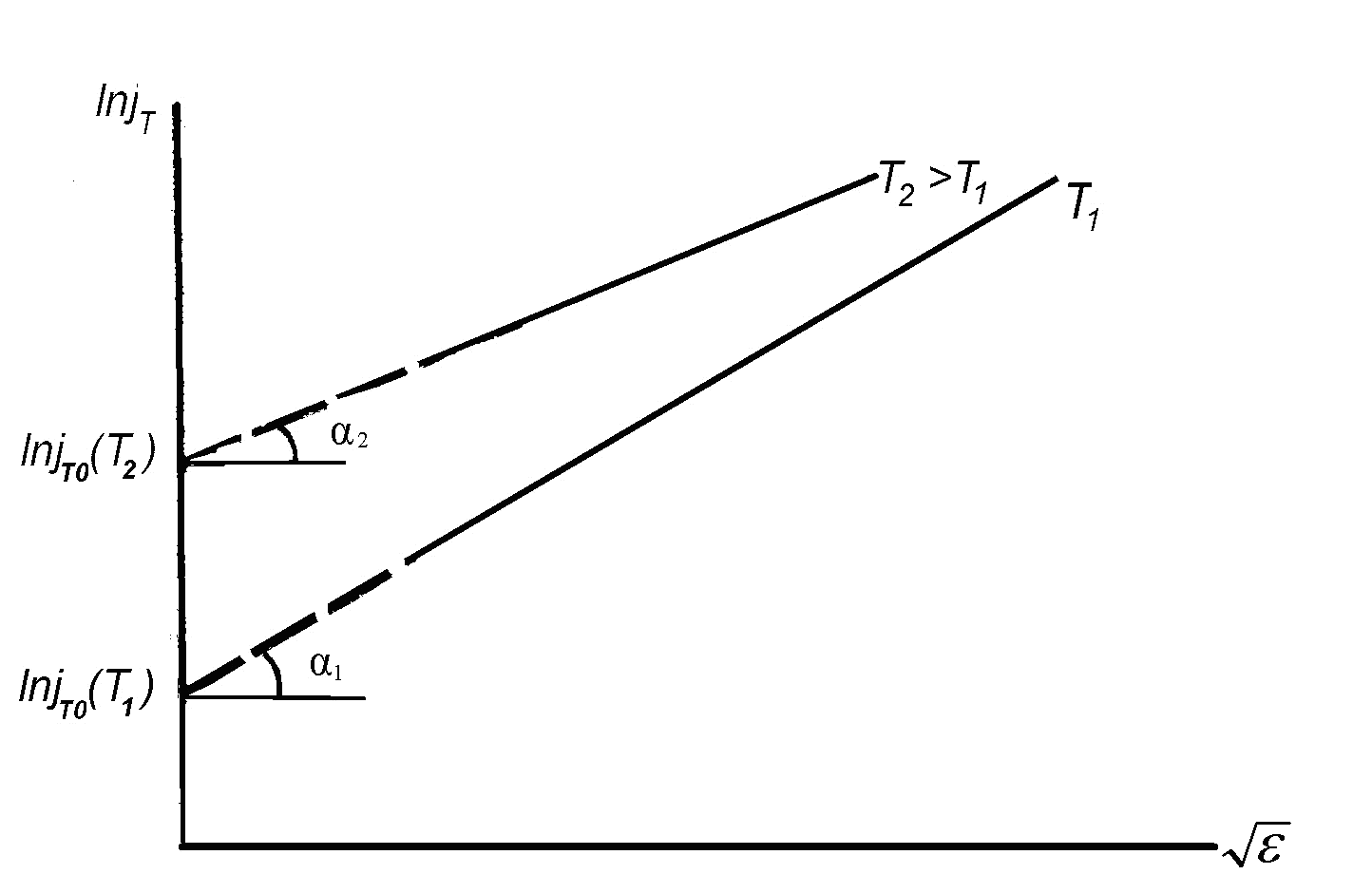
Рисунок 6- Прямые Шоттки для двух температур катода

соответствуют уравнению

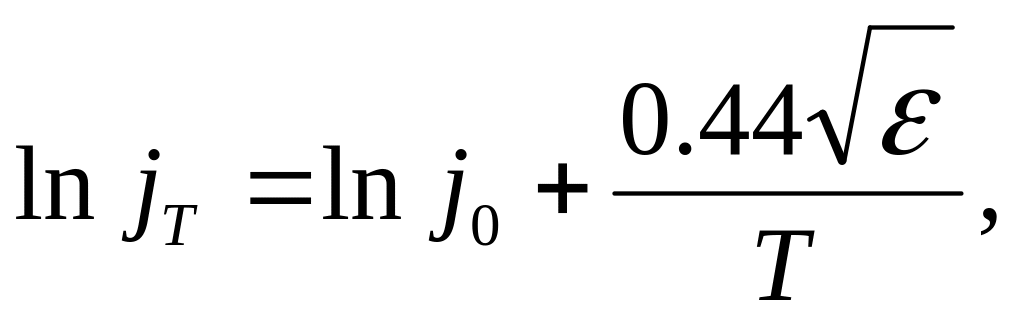(13)

где j₀- плотность тока при напряженности поля ε = 0, а

(14)

для цилиндрической системы электродов. Здесь r_k и r_a радиусы катода и анода соответственно. Отрезок j_o, отсекаемый продолжением прямолинейного участка графика Шоттки от оси ординат, и есть значение плотности тока насыщения при ε = 0.

Определение температуры катода. В данной работе температура катода определяется по методу баланса мощностей. Подводимая к катоду мощность накала Р_н=I_нV_н отводится путем излучения и теплопроводностью по держателям катода. Теплопроводность по газу и конвективная составляющая отсутствуют, так как катод находится при низком давлении. При высоких температурах и достаточно большой длине катода теплопроводностью по держателям можно пренебречь. Тогда вся мощность будет отводиться только излучением в соответствии с законом Стефана-Больцмана и можно записать

Р_н= I_нV_н=πd_kl_kεσT⁴, (15)

где d_к,l_к – диаметр и длина катода соответственно,

σ = 5,67*10^-8 – постоянная Стефана- Больцмана,

ε – степень черноты нити катода, зависящая от качества обрабатываемой поверхности и в незначительной степени от температуры.

Из этого соотношения можно определить температуру катода

T=( Р_н/ πd_kl_kεσ)^1/4 (16)

Экспериментальная установка

В работе используется специальный вакуумный прибор с коаксиальными цилиндрическими электродами (анод и охранные кольца) и вольфрамовым прямонакальным катодом. Параметры указываются преподавателем.

Схема измерений приведена на рисунке 7. Анодное напряжение

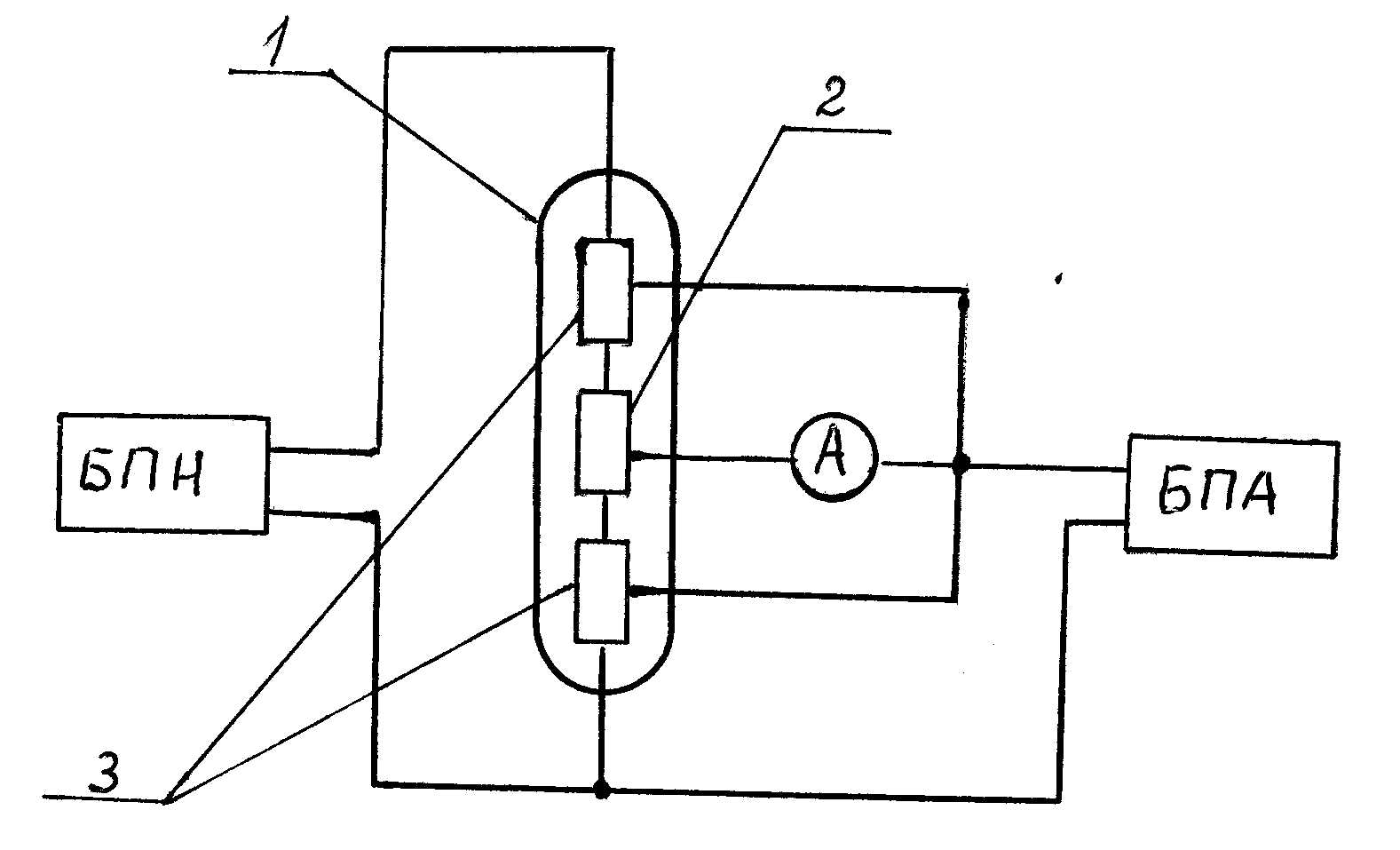
Рисунок7-Схема включения лампы с охранными кольцами:

1 – корпус лампы, 2 – анод, 3 – охранные кольца

подается от источника питания, регулируется потенциометром R1 и контролируется вольтметром PV1. Анодный ток измеряется мультиметром типа В7-16А. Амперметр РА2 и вольтметр PV2 служат для определения мощности, расходуемой на нагрев катода, что необходимо при расчете его температуры.

Проведение эксперимента

1. Собрать (проверить) схему для проведений измерений согласно рисунку 7.

2. Снять вольт-амперные характеристики исследуемой лампы при трех значениях напряжения накала (минимальном, среднем и максимальном (уточняются у преподавателя).

3. Построить график вольт-амперной характеристики для опыта с наибольшим напряжением накала и определить V^*_a.

4. Установить найденное значение V^*_a на аноде экспериментального прибора.

5. Определить значения I_T при разных Р_н (10-12 значений).

6. Результаты работы показать преподавателю.

7. Выключить установку.

Обработка результатов

1. Построить зависимости I_а=f(V_а) по данным пункта 2 и определить значения I_T методом касательных.

2. Рассчитать по формуле (16) значения температуры катода для всех значений мощности накала и построить график j_T=f(Т). Степень черноты катода принять равным 0,3.

3. Рассчитать и построить для трех значений тока накала (пункт 2)

графики Шоттки и определить j₀. Сравнить с полученными по перегибу ВАХ значениями.

4. Построить прямую Ричардсона lg (j_T/T²)=f(5040/T), и определить значения А и φ₀.

5. Сравнить с табличными значениями и указать вероятные источники погрешности.

Контрольные вопросы

1. Нарисуйте потенциальный барьер на границе металл-вакуум и объясните причины его появления.

2. Поясните понятие полной и эффективной работы выхода.

3. Напишите и поясните уравнение термоэмиссии металлов.

4. Как определяется температура катода в данной работе? Назовите причины погрешности используемого метода.

5. Поясните способы определения тока насыщения I_T и источники погрешности.

6. Поясните метод прямой Ричардсона и назовите погрешности определения констант А и φ₀.

Литература

1. Сушков А.Д. Вакуумная электроника: Физико-технические основы. – СПб.: Издательство «Лань», 2004. –464 с.

2. Фридрихов С.А., Мовнин С.М. Физические основы электронной техники.- М.: Высшая школа, 1982. – 608с.

3. Соболев В.Д. Физические основы электронной техники. – М.: Высшая школа, 1979. – 376 с.