Министерство образования и науки РФ

Северо-Кавказский горно-металлургический институт (ГТУ)

Кафедра Электронных приборов

Методические указания к лабораторным работам

по дисциплине

ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОНИКИ

Ч.1

для направления подготовки (специальности)

210100 Электроника и наноэлектроника

Составитель:

В.В.Перепелицын

Владикавказ 2013 Содержание

Лабораторная работа №1. Определение энергии активации и температурного коэффициента сопротивления полупроводника

Лабораторная работа № 2. Определение концентрации и параметров электронного переноса полупроводника методом Холла ……………………………………………………………………………

Лабораторная работа №3. Определение времени жизни неравновесных носителей заряда …………………………………….

Лабораторная работа № 4. Исследование термоэлектронной эмиссии металлов………………………………………………………

Список рекомендуемой литературы………………………………

Структура отчета………………………………………………….

Лабораторная работа №1 Определение энергии активации и температурного коэффициента сопротивления полупроводника

Цель работы: экспериментальное определение несколькими методами энергии активации, коэффициента температурной чувствительности и температурного коэффициента сопротивления полупроводника по температурной характеристике образца.

Теоретическое введение

Собственные и примесные полупроводники. Все вещества по электрофизическим свойствам могут быть разделены на три больших класса: металлы, полупроводники и диэлектрики. Одна из систем классификации веществ - по величине удельного электрического сопротивления. У металлов оно находится в пределах 10^-8 - 10^-6 Омм. Вещества с удельным сопротивлением более 10⁸ Омм относятся к диэлектрикам. А вещества с удельным сопротивлением от 10^-6 до 10⁸ Омм отнесены к полупроводникам. По этому параметру четко выраженной границы между металлами, полупроводниками и диэлектриками не существует, а потому значения удельного сопротивления не могут служить в качестве однозначного критерия для классификации веществ. Поэтому у разных авторов эти границы несколько отличаются.

С учетом ряда других факторов для полупроводников можно принять следующее определение: полупроводники - это такие материалы, удельное сопротивление которых при комнатной температуре лежит в пределах от 10^-6 до 10⁸ Омм, сильно зависит от структуры вещества, вида и количества примеси и от внешних условий: температуры, освещения, электрического и магнитного полей.

Механизм электропроводности чистых одноатомных полупроводников, например кремния и германия, легко понять из следующих модельных представлений: при абсолютном нуле в полупроводниках валентная зона заполнена, а зона проводимости свободна (рисунок 1, а). Поэтому при Т = 0 К собственный полупроводник, как и диэлектрик, обладает нулевой проводимостью.

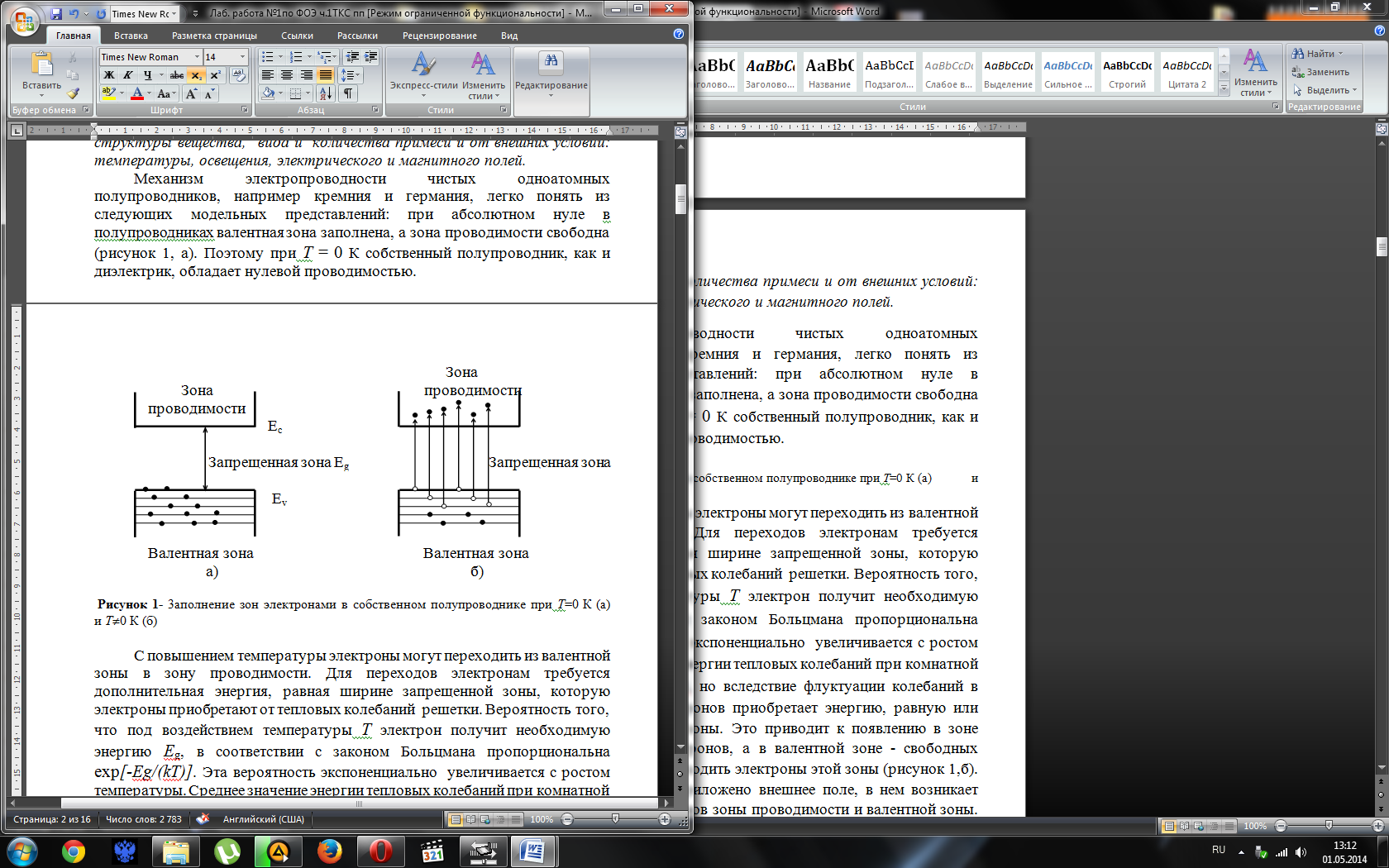
Рисунок 1- 3аполнение зон электронами в собственном полупроводнике при Т=0 К (а) и Т0≠ К (б)

С повышением температуры электроны могут переходить из валентной зоны в зону проводимости. Для переходов электронам требуется дополнительная энергия, равная ширине запрещенной зоны, которую электроны приобретают от тепловых колебаний решетки. Вероятность того, что под воздействием температуры Т электрон получит необходимую энергию E_g, в соответствии с законом Больцмана пропорциональна exp[-Eg/(kT)]. Эта вероятность экспоненциально увеличивается с ростом температуры. Среднее значение энергии тепловых колебаний при комнатной температуре E = kT = 26 мэВ, но вследствие флуктуации колебаний в решетке некоторая часть электронов приобретает энергию, равную или больше ширины запрещенной зоны. Это приводит к появлению в зоне проводимости свободных электронов, а в валентной зоне - свободных уровней, на которые могут переходить электроны этой зоны (рисунок 1,б). Если же к такому кристаллу приложено внешнее поле, в нем возникает направленное движение электронов зоны проводимости и валентной зоны. Это приводит к появлению электрического тока. Кристалл становится проводящим. Чем уже запрещенная зона и выше температура кристалла, тем больше электронов переходит в зону проводимости и тем более высокую электропроводность приобретает кристалл.

Анализ поведения электронов в валентной зоне при действии внешнего поля приводит к выводу, что суммарный ток всех электронов валентной зоны, имеющей одно вакантное состояние, эквивалентен току, обусловленному движением одной частицы с положительным зарядом +e, помещенной в это состояние. Такую фиктивную частицу называют дыркой. Дырке следует приписать положительную эффективную массу, численно равную отрицательной эффективной массе электрона у потолка валентной зоны.

Рассмотрим теперь механизм электропроводности полупроводника из атомов IV группы, в решетке которого один из атомов заменен атомом элемента V группы, например мышьяка в решетке кремния. Полупроводник, имеющий примеси, называют примесным, а его электропроводность, обусловленную наличием в кристалле примеси - примесной. В решетке кремния четыре валентных электрона мышьяка вместе с четырьмя электронами ближайших атомов кремния участвуют в образовании ковалентной связи. Пятый электрон мышьяка, не принимающий участия в образовании ковалентной связи, слабо связан с атомом мышьяка. При низких температурах пятый электрон локализован около атома мышьяка, но при повышенных температурах он отщепляется от примеси и свободно перемещается по кристаллу. Атом мышьяка, отдавший электрон, превращается в положительный ион.

Наряду с ионизацией примеси может происходить и ионизация атомов основного вещества. Но в области низких температур доминирующим процессом будет ионизация атомов примеси. Свободных электронов в зоне проводимости будет больше, чем дырок в валентной зоне. Электроны будут играть доминирующую роль в проводимости полупроводника, поэтому их называют основными носителями заряда, а дырки - неосновными носителями заряда. Такой полупроводник называют электронным, донорным или n-типа.

Наличие примеси в кристалле полупроводника будет характеризоваться появлением локальных уровней, лежащих в запрещенной зоне. Так как для ионизации атома мышьяка требуется меньшая энергия E_d, чем для разрыва ковалентных связей кремния, то энергетический уровень донорной примеси E_d должен располагаться в запрещенной зоне в непосредственной близости к краю зоны проводимости E_d ≈0,01 эВ (рисунок 2,а).

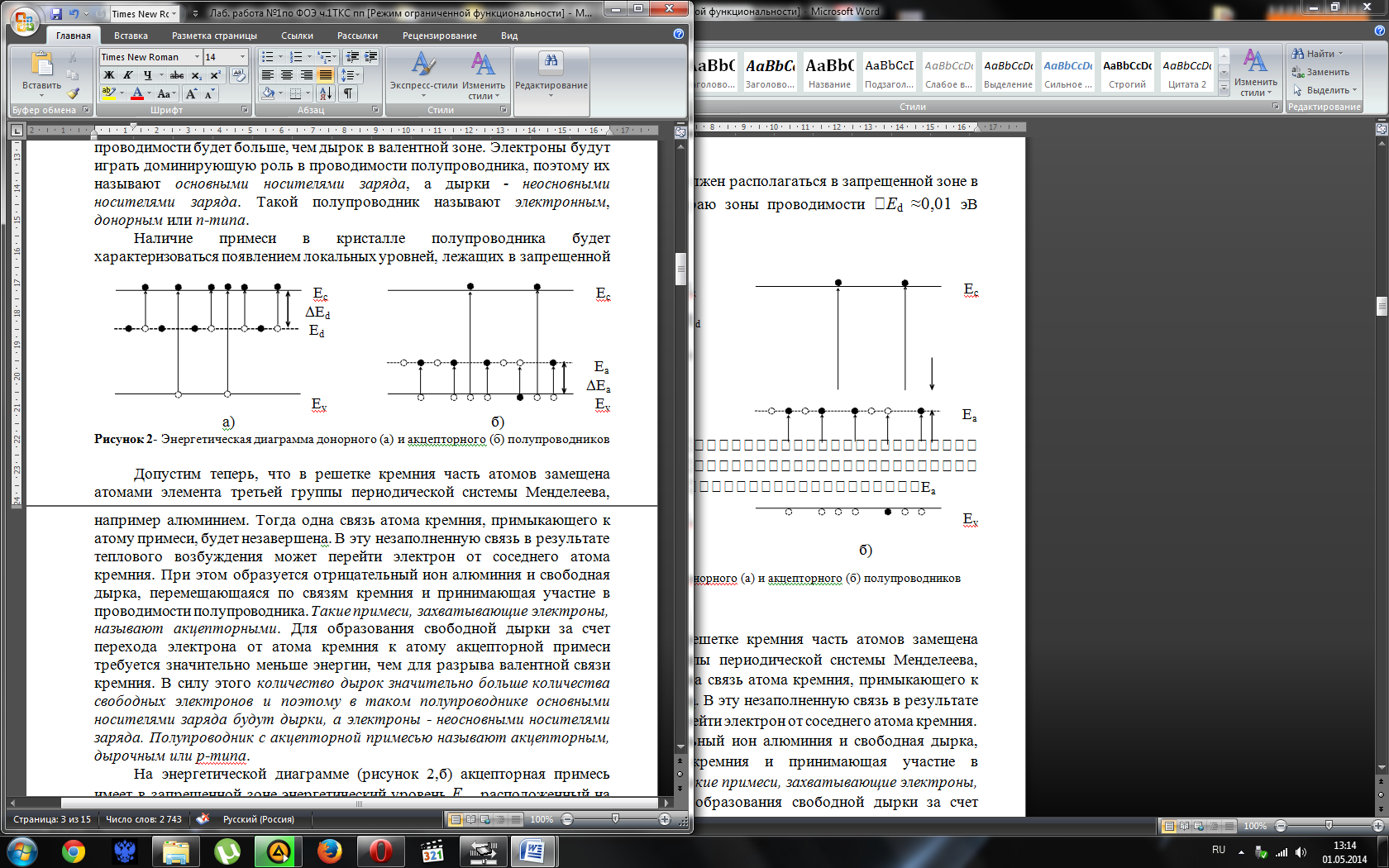
Рисунок 2- Энергетическая диаграмма донорного (а) и акцепторного (б) полупроводников

Допустим теперь, что в решетке кремния часть атомов замещена атомами элемента третьей группы периодической системы Менделеева, например алюминием. Тогда одна связь атома кремния, примыкающего к атому примеси, будет незавершенa. В эту незаполненную связь в результате теплового возбуждения может перейти электрон от соседнего атома кремния. При этом образуется отрицательный ион алюминия и свободная дырка, перемещающаяся по связям кремния и принимающая участие в проводимости полупроводника. Такие примеси, захватывающие электроны, называют акцепторными. Для образования свободной дырки за счет перехода электрона от атома кремния к атому акцепторной примеси требуется значительно меньше энергии, чем для разрыва валентной связи кремния. В силу этого количество дырок значительно больше количества свободных электронов и поэтому в таком полупроводнике основными носителями заряда будут дырки, а электроны - неосновными носителями заряда. Полупроводник с акцепторной примесью называют акцепторным, дырочным или р-типа.

На энергетической диаграмме (рисунок 2,б) акцепторная примесь имеет в запрещенной зоне энергетический уровень E_a , расположенный на небольшом расстоянии над потолком валентной зоны E_a≈0,01 эВ. При ионизации акцепторной примеси происходит переход электрона из валентной зоны на уровень E_a , а в валентной зоне появляется вакантная ковалентная связь - дырка, которая и является свободным носителем заряда.

В полупроводнике могут одновременно присутствовать как донорная, так и акцепторная примеси.

Концентрация носителей заряда в полупроводниках. Возникновение свободных носителей заряда в полупроводниках обусловлено "отрывом" электрона от основного или примесного атома. Чтобы такой процесс произошел, необходимо передать электрону достаточно большую порцию энергии E_a , которую принято называть энергией активации. В статистической физике показывается, что вероятность получения частицей коллектива порции энергии E_a при средней тепловой энергии kT пропорциональна exp (-E_a / kT)

. (1)

Следовательно, число свободных электронов (или электронно - дырочных пар в собственном полупроводнике) N, создаваемых каждую секунду в единице объема полупроводника, равняется

, (2)

где K - коэффициент пропорциональности, различный для разных полупроводников. Поэтому концентрации электронов n и дырок p в различных полупроводниках будут описываться похожими на (2) соотношениями.

Строгий вывод соотношений для собственного полупроводника (полупроводника i-типа) приводит к формуле

, (3)

где N_c и N_v - эффективная плотность состояний в зоне проводимости и в валентной зоне соответственно. Следовательно, для собственного полупроводника энергия активации проводимости E_a = E_g / 2 .

В системе СИ после подстановки констант в выражения для N_c и N_v получим

, (4)

где m_n , m_p и m - эффективные массы электрона, дырки и масса свободного электрона соответственно.

Таким образом, концентрация носителей заряда в невырожденном собственном полупроводнике зависит от температуры T, ширины запрещенной зоны E_g , значений эффективных масс электронов m_n и дырок m_p. Температурная зависимость собственной концентрации носителей заряда при E_g>>kT определяется в основном экспоненциальным членом в соотношении (4).

Для практики всегда удобнее использовать линейные зависимости как более простые для построения графиков и анализа. Экспоненциальные зависимости "выпрямляют" путем логарифмирования.

Логарифмический масштаб позволяет не только "выпрямить" экспоненту, но и отразить изменения функции в существенно большем интервале, чем при линейном масштабе. Зависимость ln n_i = f (1/T) будет практически линейной (рисунок 3), так как

. (5)

Строго говоря, первый член равенства (5) зависит от температуры, как это видно из (4). Но эта зависимость по сравнению со вторым членом настолько слабая, что в ограниченном интервале температур ее можно не учитывать. По наклону прямой легко определить ширину запрещенной зоны, так как угловой

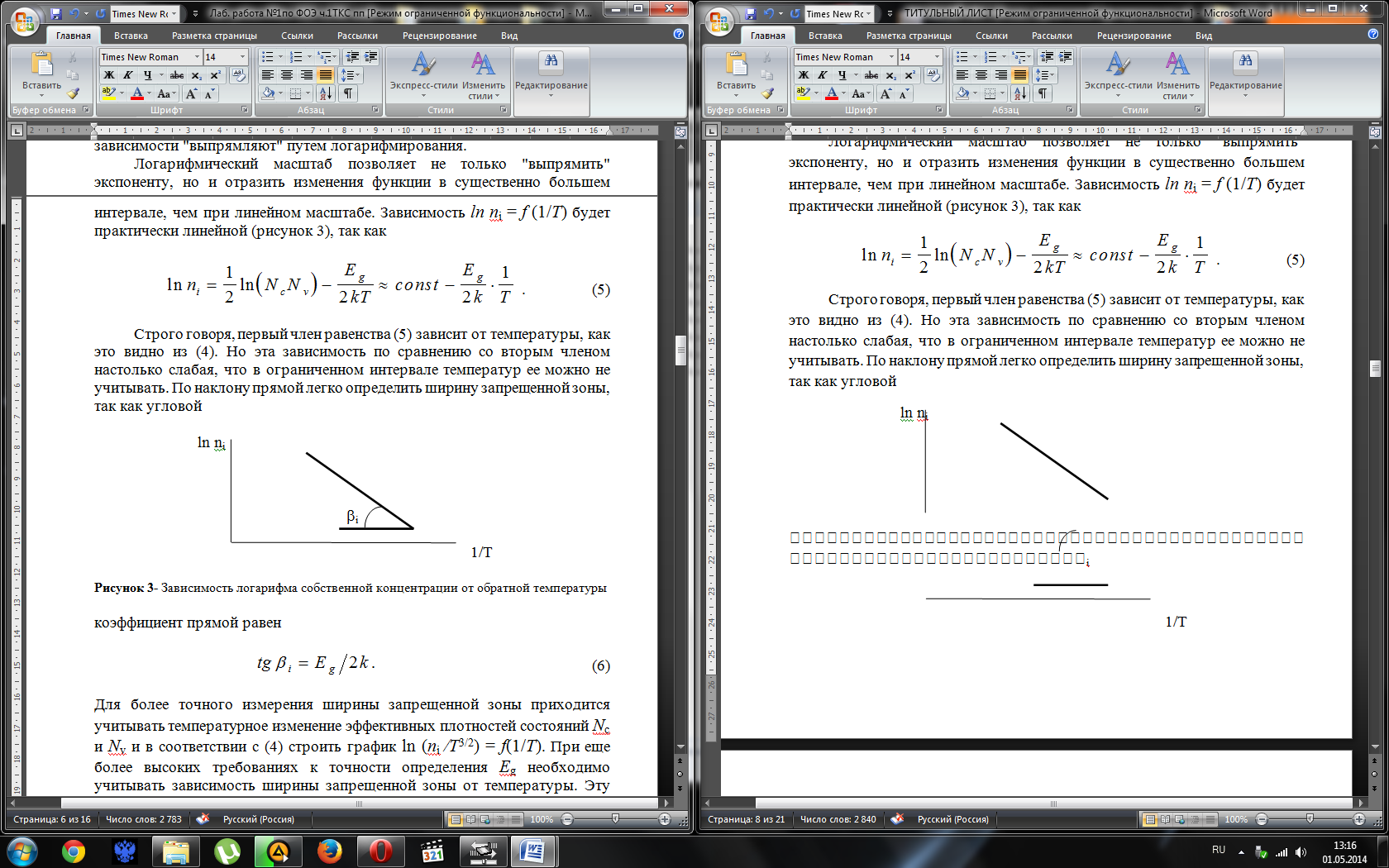
Рисунок 3- Зависимость логарифма собственной концентрации от обратной температуры

коэффициент прямой равен

(6)

Для более точного измерения ширины запрещенной зоны приходится учитывать температурное изменение эффективных плотностей состояний N_c и N_v и в соответствии с (4) строить график ln (n_i ∕T^3/2) = f(1/T). При еще более высоких требованиях к точности определения E_g необходимо учитывать зависимость ширины запрещенной зоны от температуры. Эту зависимость для германия и кремния в диапазоне температур 175 - 350 K можно описать линейным законом вида:

, (7)

где E_g0 - экстраполированная ширина запрещенной зоны при 0 K, a  = dE_g / dT < 0 - температурный коэффициент изменения ширины запрещенной зоны. Для германия, кремния и арсенида галлия он равен 3,910^-4; 2410^-4 и 4310^-4 эВ/К соответственно.

Рассмотрим теперь электронный (донорный) полупроводник. Процесс образования свободных носителей заряда проанализируем сначала качественно. При очень низких температурах, близких к 0 К, средняя тепловая энергия kT электронов мала. Поскольку энергия активации примеси (энергия ионизации) E_d обычно много меньше ширины запрещенной зоны E_g , то электроны в зону проводимости будут переходить только с уровня донора E_d. Равновесная концентрация этих "примесных" электронов в зоне проводимости определится из выражения, аналогичного формуле (3)

, (8)

где N_d - концентрация атомов донорной примеси.

В формуле (8) в показателе экспоненты стоит величина E_d , а не E_g , как в формуле (3), определяющей концентрацию собственных носителей.

При повышении температуры T до значения, при котором kT > E_d, все примесные атомы оказываются ионизованными и концентрация примесных электронов просто равняется N_d . Это явление носит название "примесное истощение". Условную температуру, при которой начинается участок примесного истощения, часто обозначают T_s и называют температурой истощения примеси.

Дальнейшее повышение температуры приводит к ионизации атомов полупроводника, т.е. к переходу электронов из валентной зоны в зону проводимости. Поскольку концентрация этих атомов много больше концентрации донорных атомов, то при высокой температуре большая часть электронов в зоне проводимости обусловлена валентными электронами, и концентрация определяется соотношением (3). Температура, при которой наступает собственная проводимость у донорного полупроводника, обычно обозначается как T_i . Из физических соображений очевидно, что температура T_i тем ниже, чем меньше ширина запрещенной зоны E_g и ниже концентрация примеси N_d.

График логарифма концентрации от обратной температуры в электронном (донорном) полупроводнике представлен на рисунке 4.

На графике цифрой 1 обозначена область слабой ионизации примеси. Концентрация электронов на начальном участке этой области в соответствии с приближенным соотношением (8) может быть описана выражением

. (9)

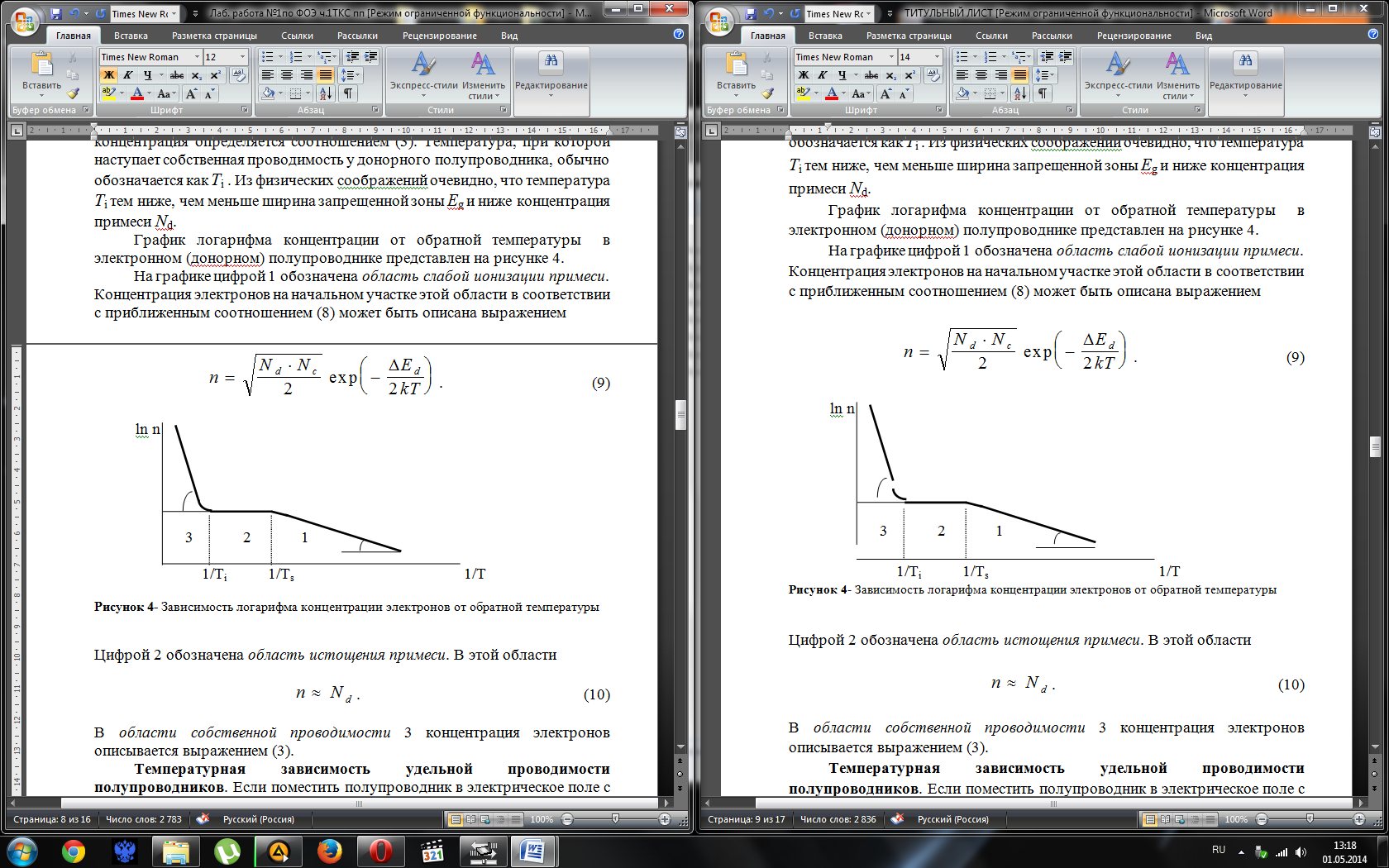
Рисунок 4- Зависимость логарифма концентрации электронов от обратной температуры

Цифрой 2 обозначена область истощения примеси. В этой области

. (10)

В области собственной проводимости 3 концентрация электронов описывается выражением (3).

Температурная зависимость удельной проводимости полупроводников. Если поместить полупроводник в электрическое поле с напряженностью , то через него будет протекать ток, который называют дрейфовым. Плотность этого тока определяется законом Ома в дифференциальной форме

, (11)

где  - удельная электрическая проводимость (электропроводность) полупроводника. В полупроводнике в общем случае удельная проводимость имеет две составляющие - электронную _n и дырочную _p т.е.

. (12)

Строгая теория для невырожденного электронного газа в полупроводнике приводит к выражению для плотности тока:

, (13)

где

, (14)

_n - подвижность электронов (скорость дрейфа в электрическом поле единичной напряженности);

< > - усредненное время релаксации, зависящее при изотропном рассеянии лишь от энергии.

Сравнивая (13) с (11), находим:

. (15)

Аналогично для дырочного полупроводника

, (16)

где < ' > - время релаксации дырок.

При изучении зависимости проводимости (сопротивления) от температуры необходимо знать зависимость = f (). Теория приводит к следующим выводам. При рассеянии носителей тепловыми колебаниями решетки _тк ~ T^-3/2 для невырожденного и для вырожденного газа. При рассеянии на ионизованных примесях _i ~ T^3/2. Подвижность носителей при наличии нескольких типов дефектов может быть описана выражением

, (17)

где _i - подвижность носителей заряда в кристалле с i-м типом дефектов.

Зависимость подвижности от температуры в невырожденных примесных полупроводниках показаны на рисунке 5.

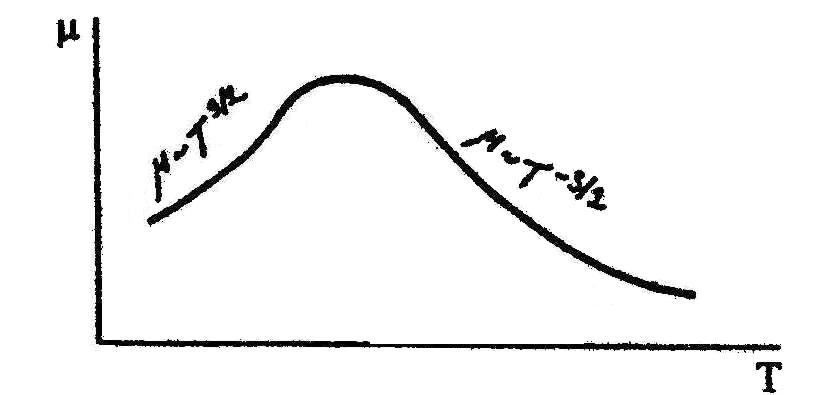
Рисунок 5- Зависимость подвижности от температуры в невырожденном полупроводнике

При высоких температурах преобладает рассеяние носителей заряда тепловыми колебаниями решетки и ~ T^-3/2, а при низких температурах определяющим является рассеяние на ионах примеси и ~ T^3/2 .

Рассмотрим теперь собственный полупроводник. В соответствии с (12), (15) и (16) для электропроводимости можно записать

. (18)

Подставив выражение (3) в (18) и обозначив через ₀ коэффициент перед экспонентой, получим

. (19)

Величина ₀ зависит от вида полупроводника и слабо зависит от температуры. После логарифмирования (19) приходим к линейной зависимости ln_i от 1/T (рисунок 6.):

, (20)

близкой к зависимости ln n_i = f (1/T). Из графика (рисунок 6) можно найти ln₀ и ширину запрещенной зоны полупроводника E_g = 2k tg _i .

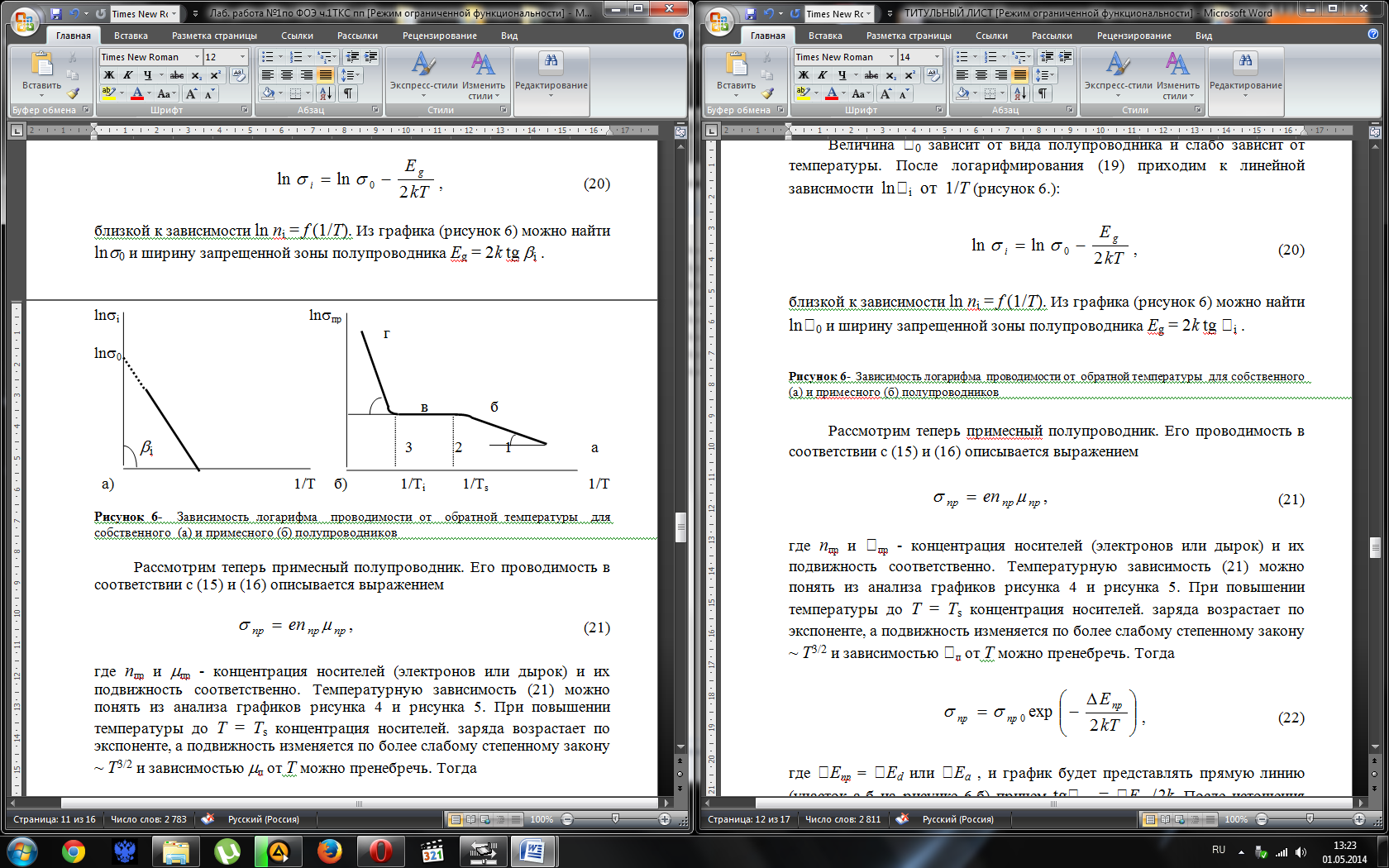
Рисунок 6- Зависимость логарифма проводимости от обратной температуры для собственного (а) и примесного (б) полупроводников

Рассмотрим теперь примесный полупроводник. Его проводимость в соответствии с (15) и (16) описывается выражением

(21)

где n_пр и _пр - концентрация носителей (электронов или дырок) и их подвижность соответственно. Температурную зависимость (21) можно понять из анализа графиков рисунка 4 и рисунка 5. При повышении температуры до T = T_s концентрация носителей. заряда возрастает по экспоненте, а подвижность изменяется по более слабому степенному закону ~ T^3/2 и зависимостью _п от Т можно пренебречь. Тогда

, (22)

где E_пр = E_d или E_a , и график будет представлять прямую линию (участок а-б на рисунке 6,б) причем tg_пр = E_пр/2k. После истощения примесных уровней в интервале температур T_s < T < T_i концентрация не изменяется и зависимость _пр(T) определяется лишь температурной зависимостью подвижности _пр(T). Так как в этой области _пр~T^-3/2, то проводимость на участке б-в будет падать пропорционально T^-3/2.

При T > T_i проводимость снова возрастает по экспоненциальному закону за счет собственной проводимости полупроводника (участок в-г):

(23)

и

. (24)