3.1.3. Заповнення зон електронами
Електропровідність твердих тіл залежить від взаємного розташування зони провідності і валентної зони. Саме за характером енергетичних діаграм тверді тіла більш чітко розділяють на провідники (метали), напівпровідники і діелектрики (ізолятори ) На рис. 1.6. зображені спрощені діаграми енергетичних рівнів металу, власного напівпровідника і діелектрика. В металах зона провідності і валентна зона перекриваються, і електрони валентної зони можуть легко переходити в зону провідності незалежно від температури тіла. В зоні провідності електрони належать всьому кристалу і вільно всередині нього переміщуються. Провідний стан для металу є звичайним.
На відміну від металів при нульовій температурі у діелектриків і напвіпровідників зона провідності порожня і електропровідність відсутня.
З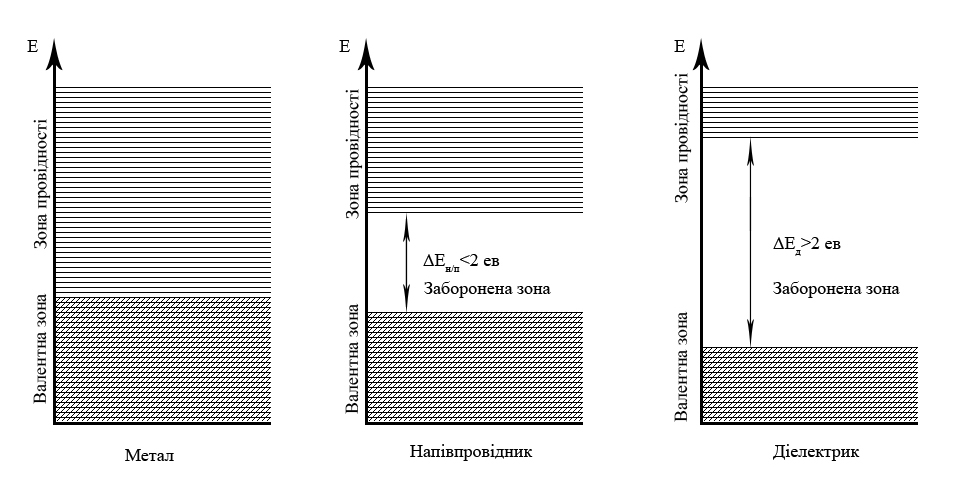
агальне
число дозволених значень енергії в
кристалі перевищує число валентних
електронів. Енергетично найбільш
вигідними рівнями є самі низькі. Але
оскільки, у відповідності з принципом
Паулі, на одному рівні не може одночасно
знаходитись більше двох електронів (з
протилежно направленими спінами), тому
електрони в кристалі навіть при Т=0 К
займають широкий діапазон енергій. В
металі вони заповнюють нижню частину
загальної зони дозволених рівнів від
нуля до деякого максимального значення
Еф
–
рівня Фермі, а верхня частина залишається
незаповненою.
Рис. 1.6.
В напівпровідниках і діелектриках електрони заповнюють всі рівні нижніх зон, а верхні зони залишаються вільними. При підвищенні температури електрони з нижньої зони можуть перейти у верхню.
Введення домішок у власний напівпровідник, тобто речовин, які відрізняються від основної речовини кристалу, приводить до появи в забороненій зоні додаткових, «локальних» енергетичних рівнів.
Дозволені енергетичні стани можуть бути заповнені електронами, або залишатись вільними.
Розподіл електронів за енергією в кристалах з виродженим електронним газом описується статистикою Фермі-Дірака і має вигляд:
,
де
-
число електронів в одиниці об’єму,
повна енергія яких знаходиться в границях
від Е до Е+dЕ;
- число квантових станів в одиниці
об’єму,
- функція Фермі, яка виражає ймовірність
того, що квантовий стан з енергією Е
зайнятий електроном;
-
стала Больцмана, Т – температура тіла.
Для металів
(3.1)
Розрахунки
за формулою (3.1) дають значення
від кількох електрон-вольт для
лужноземельних елементів до 15 еВ і
більше для важких елементів (W,
Pt,
Ni
…).
На
рис. 1.7. наведений графік функції
при Т=0 К і Т
0,
з якого видно, що навіть при низьких
температурах велика кількість електронів
має достатньо високу внутрішню енергію.
Рис. 1.7.
Підвищення температури змінює розподіл електронів за енергією тільки біля рівня Фермі. І тільки ці електрони можуть переходити на більш високі незайняті енергетичні рівні. Електрони, які займають низькі енергетичні рівні, не можуть зразу перейти на високі рівні, томі що вони зайняті іншими електронами. Тільки значне підвищення температури дозволить приймати участь у цьому процесі всім електронам. Але для більшості металів така температура вища їх температури плавлення, тому в реальних емітерах далеко не всі електрони переходять на більш високі рівні.
Розрахунки показують, що в металах електрони з достатньо великими значеннями енергії розподіляються за максвелівським законом
В напівпровідниках (власних і легованих домішками), в яких електронний газ знаходиться у невиродженому стані, закон розподілу електронів за енергією також масвелівський.