3. Приклади розв’язування задач

Приклад 1.1

Чому дорівнює поверхневий натяг бензолу, якщо він піднімається на 0,0367 м в трубці радіусом 1,84∙10^-4м; густина бензолу 880 кг/м³, густиною повітря можна нехтувати.

Поверхневий натяг при умові, що крайовий кут змочування дорівнює нулю, можна визначити за рівнянням

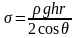
 = (880∙9,81∙1,84∙10^-4∙0,0367)/2 = 29,2 мДж/м²

Приклад 1.2

Обчисліть поверхневий натяг розчину масляної кислоти за методом Ребіндера, якщо тиск бульбашки при проскакуванні її через воду дорівнює 1,23 кПа, а через розчин масляної кислоти 1,01 кПа. Поверхневий натяг води при температурі досліду дорівнює 72,75 мН/м.

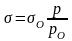
 = 72,75∙10^-3∙1,01∙10³/1,23∙10³ = 59,7 мН/м

Приклад 1.3

За допомогою сталагмометра Траубе отримані наступні результати: середнє число краплин води 54,7. Середнє число краплин досліджуваного розчину дорівнює 88,2. Температура досліду 17,5^оС. Густина розчину 1131 кг/м³, а поверхневий натяг води при даній температурі 72,38 мН/м, густина води 998,5 кг/м³. На основі цих даних обчисліть поверхневий натяг розчину.

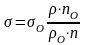
 = 72,38∙10^-3∙1131∙54,7/(998,5∙88,2) = 50,9 мН/м

Приклад 1.3

Поверхневий натяг рідкої міді при 1535^оС дорівнює 1,30 Н/м, температурний коефіцієнт поверхневого натягу -3,1∙10^-4, знайдіть поверхневу ентальпію рідкої міді.

H_s = U_s =  – T(d/dT)

H_s = 1,30 – 1808(-3,1∙10^-4) = 1,86 Н/м

Приклад 1.4

Розрахуйте роботу адгезії ртуті до скла при 293 К, якщо відомий крайовий кут змочування 130^0.. Поверхневий натяг ртуті 475 мДж/м². зайдіть коефіцієнт розтікання ртуті на поверхні скла.

Wa = (1 + cos ) = 475∙10^-3(1 – 0.64) = 171∙10^-3 Дж/м²

Wk = 2∙ = 2∙475∙10^-3 = 950∙10^-3 Дж/м²

f = Wa – Wk = 171∙10^-3 – 950∙10^-3 = -779∙10^-3 Дж/м²

Отже ртуть по поверхні скла не розтікається.

Приклад 1.6

Обчисліть надлишковий тиск всередині крапель бензолу, рівноважних з парою, якщо питома поверхня системи становить 6∙10⁸ м^-1, а поверхневий натяг бензолу 28,87 мДж/м² при 293 К .

p = 2/r

S_пит = 6D = 6/d = 3/r; r = 3/ S_пит

p = 2∙28,87∙10^-3/(3/6∙10⁸) = 11,6∙10⁶ Н/м²

Приклад 1.7

Визначте енергію Гіббса поверхні крапель водяного туману масою m = 4 г при 298 К, якщо поверхневий натяг води σ =72,7 мДж/м², густина води ρ= 0,998 г/см3, дисперсність частинок D = 5∙10⁷ м^-1

Енергія Гіббса поверхні визначається за рівнянням:

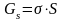
Питома поверхня дисперсної системи: 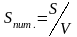для частинок сферичної форми набуває вигляд:

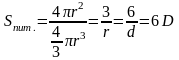
Звідки: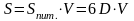

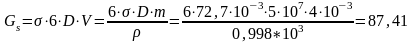Дж.

Приклад 1.8

Дві вертикальні пластинки частково занурені в рідину на відстані 1мм одна від одної. Кут змочування пластинок становить 30⁰. Поверхневий натяг рідини 65 мДж/м², різниця густин рідини та повітря 1 г/см³.

Обчисліть надлишковий тиск в рідині і силу взаємного притягання пластин, якщо їх розміри 5∙на 5 см.

Надлишковий тиск в рідині між паралельними пластинками розраховують за рівнянням

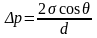= 2,65∙10^-3∙0,87/1∙10^-3 = 113 Па

При змочуванні поверхні пластинок надлишковий тиск зменшує внутрішній тиск у рідині, що призводить до її підняття порівняно з рівнем в посудині і появи сили, що стискає пластини.

F = p∙S = 113,1∙0,05∙0,05 = 0,28Н

Приклад 1.9

Обчисліть тиск насиченої пари над краплями води з дисперсністю 0,1 нм^-1 при температурі 293К. Тиск парів води над плоскою поверхнею при цій температурі 2338 Па, густина води 998 кг/м³, поверхневий натяг 72,7 мДж/м².

Вплив кривизни поверхні на тиск насиченої пари виражається рівнянням Кельвіна

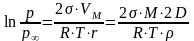
ln(p/p_∞) = (2∙0,0727∙18∙10^-3∙2∙10⁸)/(8,314∙293∙988) = 0,21

p/p_∞ = exp(0.21) =1,23; p = 1,23∙2338 = 2875 Па