3. Внутрішня енергія поверхні. Залежність поверхневого натягу від температури

Для процесів що відбуваються на поверхні внутрішня енергія одиниці поверхні U_s дорівнює:

U_s =  + TS_s =  + q_s ( 1.0),

де q_s – теплота утворення одиниці поверхні.

З врахуванням S_s = -(∂G_s/∂T)_p = -(∂/∂T)_p можна записати рівняння Гіббса - Гельмгольца для поверхневого шару:

U_s =  -T(∂/∂T)_p ( 1.0)

де (∂/∂T) = a – температурний коефіцієнт поверхневого натягу.

Рівняння температурної залежності поверхневого натягу має вигляд:

 = _o + a(T – T_o) ( 1.0)

4. Адгезія, когезія, змочування і розтікання

Взаємодію між поверхнями конденсованих тіл різної природи називають адгезією або прилипанням. Адгезійні взаємодії виникають при контакті двох конденсованих тіл, якщо відстань між ними співмірна з міжмолекулярною.

Притягання молекул і атомів всередині окремої фази називають когезією або злипанням. Це явище обумовлене міжмолекулярними силами притягання.

Рис. 1. Взаємодія між тілами різної природи.

Для системи, що складається з двох конденсованих тіл 2 і 3, що знаходяться у газовій фазі 1, з поверхневими натягами _2,1 i _3,1 , роботу адгезії W_a можна вирахувати за рівнянням Дюпре:

W_a = -G = G_поч-G_кін=_3,1+_2,1-_3,2 ( 1.0),

а роботу когезії W_K – за рівнянням:

W_K=2 ( 1.0),

де _3,2 – поверхневий натяг міжфазної поверхні.

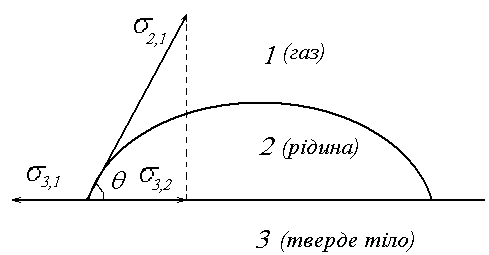
Рис. 2. Сили, що діють на краплю на поверхні.

Змочування – це поверхневе явище, яке полягає у взаємодії рідини з іншою конденсованою фазою, при умові одночасного контакту трьох фаз, одна з яких - газ (повітря).

Мірою змочування є крайовий кут змочування, це кут між площиною поверхні, що змочується і дотичною до поверхні рідини в одній із точок контуру змочування.

Для краплини (2) рис.2, яка в умовах рівноваги знаходиться на поверхні (3) в оточенні газової фази (1) крайовий кут змочування  визначається за рівнянням Юнга:

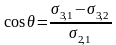( 1.0).

Параметри змочування часто зручно визначати з об’єднаного рівняння Дюпре- Юнга:

( 1.0).

Здатність рідин до розтікання характеризується різницею між роботою адгезії і когезії (коефіцієнт розтікання за Гаркінсом f) .

f =W_a-W_k=_3,1-_2,1-_2 ( 1.0)

Якщо f >0, то рідина розтікається по поверхні. Якщо f <0, то рідина знаходиться на поверхні у формі краплин.

Поверхневий натяг на межі рідина-рідина двох взаємонасичених рідин _2,1^нас дорівнює різниці поверхневих натягів їх насичених розчинів на межі з повітрям (правило Антонова).

_2,1^нас-_3,1^нас=_3,2^нас ( 1.0)

5. Вплив дисперсності на властивості тіл

Міжфазна поверхня характеризується питомою поверхнею, яка дорівнює відношенню площі міжфазної поверхні до одиниці об’єму для рідин, або одиниці маси дисперсної фази для порошків.

S_пит=S_пов/V [м²/м³=1/м], S_пит=S_пов/m [м²/кг]

Питома поверхня частинок правильної форми:

S_{пит.сфер.}=d²/(d³/6)=6/d

S_{пит.куба}=6l²/l³=6/l

З появою кривизни поверхні виникає додатковий внутрішній тиск Δр, який для сферичної поверхні дорівнює:

p_сфер=2/r ( 1.0),

а для циліндричної поверхні:

p_цил=/r ( 1.0)

Реакційна здатність G при T=const для частинок сферичної форми:

G=±2V/r ( 1.0),

плюс або мінус в рівнянні відповідають додатній, або від’ємній кривизні поверхні.

Тиск насиченої пари над викривленою поверхнею розраховується за рівнянням Кельвіна (Томсона):

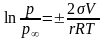( 1.0),

де - р - тиск пари над дисперсною фазою, - р_∞ - тиск пари над рівною поверхнею

Рівняння Кельвіна (Томсона) для розчинності дрібних частинок має вигляд:

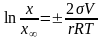( 1.0),

де - x - розчинність частинок дисперсної фази, фази а x_∞ - розчинність крупної фази; відношення x/x_∞=γ називають ступенем пересичення.