4. Приклади розв’язування задач

Приклад 4.1.

У три колби налито по 100 см³ золю Fe(OH)₃. Щоб викликати коагуляцію золю, потрібно додати: в першу колбу 10,5см³ розчину KCl концентрацією С(KCl)=1М; у другу колбу – 62,5см³ розчину Na₂SO₄; концентрацією С(½Na₂SO₄)=0,01М; у третю колбу – 37,0 см³ розчину Na₃PO₄ концентрацією С(¹/₃Na₃PO₄)=0,001М. Обчисліть пороги коагуляції і визначте знак заряду частинок золю.

Визначаємо, скільки молів KCl міститься в 10,5см³ розчину KCl концентрацією С(KCl)=1М:

моль

Визначаємо загальний об’єм розчину (золь і розчин електроліту):

дм³.

Обчислюємо поріг коагуляції електроліту KCl

моль/ дм³

Подібним чином розраховуємо пороги коагуляції для Na₂SO₄ і Na₃PO₄

моль

моль/ дм³

моль

моль/ дм³

Електроліти KCl, Na₂SO₄ і Na₃PO₄ містять катіони з однаковим зарядом, а заряд їх аніонів різний. Чим більший заряд аніона, тим поріг коагуляції стає меншим. Найменший поріг коагуляції і, відповідно, найбільша коагулюючи здатність у іонів . На основі отриманих результатів можна зробити висновок, що частинки золю Fe(OH)₃ заряджені позитивно.

Приклад 4.2.

На коагуляцію золю йодиду срібла з 1,0·10^-2 м³ стічних вод витратили 8,0·10^-4 м³ 10%-го розчину NaCl (густина 1,07·10³ кг/м³). Розрахуйте розхід 28%-го розчину Al₂(SO₄)₃ (густина 1,30·10³ кг/м³) для вилучення AgI з 100 м³ стічних вод, якщо електричний заряд колоїдних частинок йодиду срібла в цих водах: а) додатній; б) від’ємний.

Кількість молів n NaCl в 8,0·10^-4 м³ 10%-го розчину NaCl: n₁=v₁·ρ₁·g₁ (100·М₁) = 8,0·10^-4·1,07·10^-3·10/(100·0,0586) = 1,46 моль, де: v₁; ρ₁; g₁ – відповідно об’єм (м³), густина (кг/м³) та концентрація, (%) розчину NaCl; М₁ – молярна маса NaCl (кг/моль). Звідси поріг коагуляції стічних вод

ммоль/м³

де: V – об’єм зразка колоїдної системи; V_е – об’єм розчину електроліту коагулятора.

Якщо електричний заряд колоїдних частинок додатній, то іонами-коагуляторами в Al₂(SO₄)₃ будуть іони (z=2). Поріг коагуляції розглянутого гідрозолю за іонами

моль/м³

Отже, для коагуляції 100 м³ стічних вод знадобиться іонів

n₂ = 2,12 · 100 = 212 моль

Маса , що містить таку кількість іонів

кг

де: М₂ – молярна маса Al₂(SO₄)₃ (кг/моль); n₂ – кількість молів Al₂(SO₄)₃; 3 – число іонів в молекулі Al₂(SO₄)_3.

Об’єм, що містить таку масу солі:

м³

де ρ₁ і g₁ –густина (кг/м³) та концентрація, (%) розчину Al₂(SO₄)_3.

При від’ємному заряді колоїдних частинок, іонами коагуляторами в Al₂(SO₄)₃ стануть (z=3). Поріг коагуляції гідрозолю, що розкладається на іони

моль/м³

До коагуляції стічних вод у цьому випадку знадобиться іонів n₂ =0,186 · 100 = 16,6 моль. Маса , що містить таку кількість іонів

кг

де: 2 – число іонів в молекулі Al₂(SO₄)_3.

Об’єм, що містить таку масу солі:

м³

Приклад 4.3.

Експериментально отримана залежність загальної кількості n_∑ частинок гідрозолю золота в 1 м³ від часу коагуляції τ, викликаної електролітом KCl. В’язкість середовища η=1,8·10^-3 Па·с, температура Т=293 К.

τ, с	0	125	250	375	425
n∑ ∙ 10-14, част/м-3	20,2	8,08	5,05	3,67	3,31

1. Перевірте застосовність теорії Смолуховського для опису кінетики коагуляції даного золю.

2. Обчисліть час половинної коагуляції з експериментальними даними.

3. Розрахуйте константу швидкості коагуляції за експериментальними даними й порівняйте її з розрахованою теоретично, зробіть висновки.

4. Розрахуйте й побудуйте криві зміни числа первинних, подвійних і потрійних частинок з часом.

Використовуємо прямолінійнійну форму залежності загальної кількості частинок від часу : .

Обчислюємо значення n₀/n_∑ при різному часі коагуляції:

τ, с	0	125	250	375	425
n0/n∑	1	2,5	4,0	5,5	6,1

Будуємо графік залежності n₀/n_∑ = f(τ).

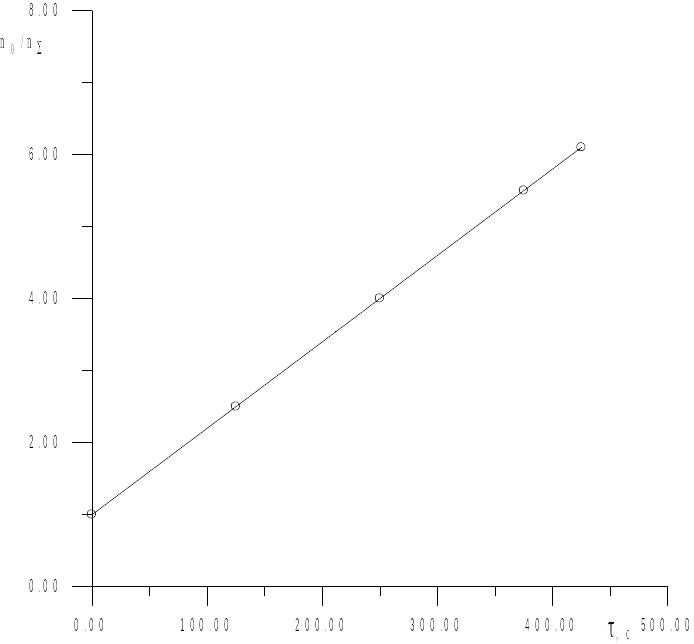
Рис. 15. Залежність загальної кількості частинок від часу.

Як видно з графіка, експериментальні дані відповідають лінійній залежності, що вказує на застосовність рівняння Смолуховського.

Із графіка знаходимо с.

Експериментальна та теоретично розрахована константи швидкості коагуляції рівні:

м³/с;

м³/с

Величини констант швидкі коагуляції є близькі, таким чином коагуляція гідрозолю золота є швидкою.

Кінетична зміна загального числа частинок в теорії Смолуховського описується рівнянням: .

Для розрахунку кількості подвійних і потрійних частинок використовуємо рівняння:

Та будуємо графік залежності кількості частинок від часу n = f(τ).

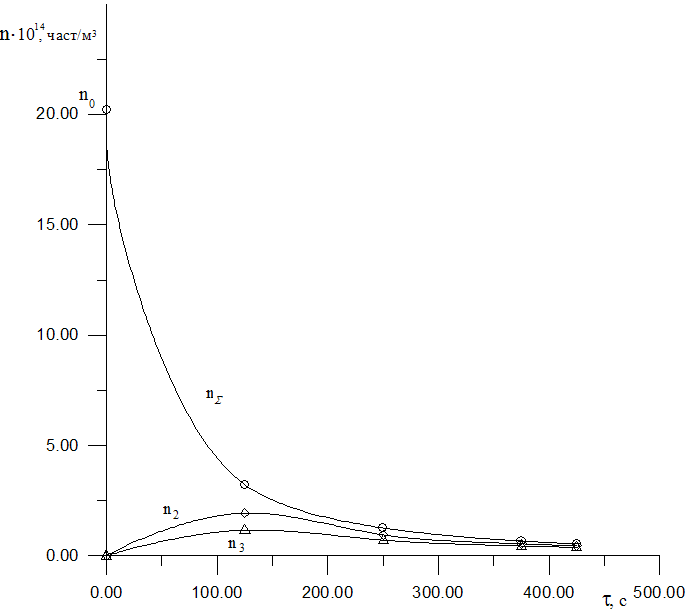
Рис. 16. Залежність кількості частинок від часу.

Приклад 4.4.

Розрахуйте і побудуйте потенціальну криву взаємодії частинок у водному розчині NaCl, якщо потенціал φ_δ = 20 мВ, константа Гамакера А=0,4·10¹⁹ Дж, параметр χ = 1·10⁸ м^-1 і температура 293 К. Значення сумарної енергії взаємодії частинок визначте при відстанях між їх поверхнями (h): 4; 8; 12; 18; 24; 32 нм.

Значення сумарної енергії взаємодії частинок розраховують додаванням енергії електростатичного відштовхування U_e і енергії молекулярного притягання U_М:

Для малих значень потенціалу поверхні (φ_δ ≤ 25мВ) енергія відштовхування частинок дорівнює:

Відносна діелектрична проникність води ε, = 81; електрична стала ε₀=8,854·10^-12 Ф/м. Енергія відштовхування частинок при відстані між її поверхнями h = 4нм дорівнює :

= 3,85·10^-5 Дж

Енергія U_М змінюється обернено пропорційно квадрату відстані між частинками. На відстані 4 нм ця енергія буде рівна:

Дж

Відповідно, сумарна енергія взаємодії частинок на відстані 4 нм буде рівна:

Дж

Аналогічно розраховуємо енергію взаємодії частинок при інших відстанях, отримані дані заносимо в таблицю:

h, нм	Дж	Дж	Дж
4	3,85	-6,63	-2,78
8	2,58	-1,66	0,92
12	1,73	-0,74	0,99
18	0,95	-0,33	0,62
24	0,52	-0,18	0,34
32	0,23	-0,10	0,13

За даними розрахунків будуємо графік залежностей =f(h).

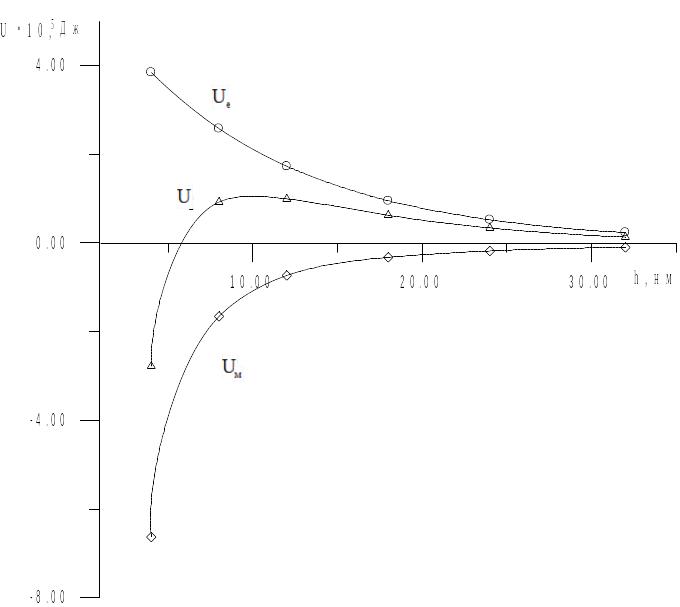
Рис. 17. Залежність енергії взаємодії частинок від відстані.

Приклад 4.5

Порівняти інтенсивності світлорозсіювання емульсій бензолу у воді (показник заломлення n₁ = 1,50) і н-пентану у воді (n₂ = 1,36) при 293 К. Показник заломлення води n₃ = 1,33. Розмір частинок і концентрації емульсій однакові.

Відношення інтенсивностей світлорозсіювання розраховуємо за рівнянням:

Емульсія бензолу розсіює світло в 30,8 рази інтенсивніше, ніж емульсія н-пентану.