Пространственный график

С помощью этого графика можно реализовать различные способы представления ЗD диаграммы рассеяния. Для этого предусмотрена возможность расположения плоскости Х- Y на выбранном пользователем уровне вертикальной оси Z (которая проходит через середину плоскости).

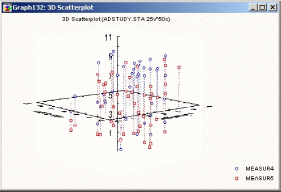
Рисунок 48. Пример пространственного графика

Хотя пространственные графики используются для тех же типов данных, что и XYZ диаграммы рассеяния, их представление может облегчить исследование некоторых трехмерных наборов данных. Рекомендуется сопоставлять данные отдельным осям на графике таким образом, чтобы переменную, структуру связей которой необходимо выделить, обозначить как Z. Тогда, перемещая плоскость XY вдоль оси Z и интерактивно вращая изображение, можно попробовать найти такой уровень Z, на котором изменяется структура связей между Х и Y (или Х, Y и Z).

Другое приложение пространственных графиков — наглядное представление плотности и направленности отклонений от определенного уровня (уровня отклонений).

Спектральная диаграмма

Первоначально этот тип графиков применялся в спектральном анализе для исследования нестационарных временных рядов, например, речевых сигналов. На горизонтальных осях можно откладывать частоты спектра и последовательные временные интервалы, а на оси Z — спектральные плотности для каждого интервала.

На этом типе графиков трехмерное пространство разделено на области, в которых данные «сжаты» в соответствующие спектральные плоскости. Обратите внимание, что для построения функциональных зависимостей (таких как в спектральном анализе) необходимо упорядочить данные таким образом, чтобы переменная Н содержала категоризующую информацию (то есть была группирующей переменной).

Спектральные диаграммы имеют явные преимущества перед обычными ЗD диаграммами рассеяния, когда необходимо исследовать, каким образом изменяется взаимосвязь между двумя переменными при различных значениях третьей переменной. Это преимущество ясно видно на приведенных ниже двух изображениях одного и того же набора данных.

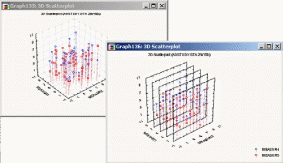
Рисунок 49. Пример трехмерной спектральной диаграммы

Трехмерные диаграммы отклонений

На этом типе графиков точки данных (заданные координатами X, Y и Z) представлены в виде «отклонений» от определенного базового уровня на оси Z.

Рисунок 50. Пример трехмерной диаграммы отклонений

Диаграммы отклонений похожи на пространственные графики. Однако на них в отличие от последних «плоскость отклонений» «невидима» и не обозначена положением плоскости Х-Y (эти оси здесь всегда находятся в стандартном нижнем положении). С помощью диаграммы отклонений можно исследовать природу трехмерных наборов данных, изображая их в виде отклонений от произвольного (горизонтального) уровня. Как упоминалось выше, такой метод «сечения» может выявить динамические связи между исследуемыми переменными.

Графики поверхности

Для построения поверхности используется подгонка по точкам трехмерного графика рассеяния. Такое представление, как и ЗD диаграммы рассеяния, позволяет выявить скрытую структуру данных и взаимосвязи между тремя переменными.

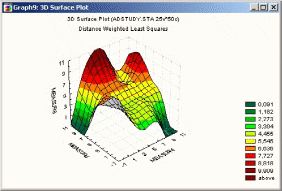
Рисунок 51. Пример трехмерного график поверхности

Графики поверхности используются в разведочном анализе данных, как и описанные в предыдущем разделе трехмерные диаграммы рассеяния. Кроме того, они полезны для наглядного представления результатов анализа, таких как подгонка пользовательской функции или кластерный анализ.