График поверхности

На последовательном графике к точкам исходных данных подгоняется сглаженная сплайнами поверхность.

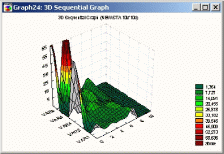
Рисунок 38. Пример графика поверхности

Последовательные значения каждой серии откладываются по оси X, а сами последовательные серии представлены на оси Y.

Гистограммы двух переменных

Трехмерные, или ЗD, гистограммы двух переменных используются для визуализации табулированных значений двух переменных или для визуализации таблиц сопряженности двух переменных. Их можно рассматривать как сочетание двух простых гистограмм (то есть гистограмм одной переменной), соединенных таким образом, чтобы можно было исследовать частоты совместного появления значений двух переменных.

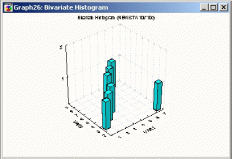
Рисунок 39. Пример гистограммы двух переменных

Распределение частот на трехмерных гистограммах вызывает интерес по двум причинам:

•  по форме распределения можно сделать вывод о природе исследуемой переменной (например, если распределение бимодально, то можно предположить, что выборка не является однородной и состоит из наблюдений, принадлежащих двум совокупностям, которые приблизительно нормально распределены);

•  многие статистики основаны на определенных предположениях о распределениях анализируемых переменных; ЗD гистограммы двух переменных помогают проверить выполнение этих предположений для пары переменных. 

Трехмерные диаграммы диапазонов

Подобно статистическим 2D диаграммам диапазонов трехмерные диаграммы диапазонов отображают диапазоны значений или столбцы ошибок, соответствующих определенным точкам данных.

Диапазоны или столбцы ошибок не вычисляются по данным, а определяются исходными значениями выбранных переменных. Для каждого наблюдения строится один диапазон или столбец ошибок. Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от средней точки. На графике можно представить одну или несколько переменных.

В основном диаграммы диапазонов используются для изображения: а) диапазонов значений для отдельных элементов анализа (наблюдений, выборок и т. д.) или б) вариации значений в отдельных группах или выборках (последнее имеет смысл, когда величины вариации получены при независимых измерениях; иначе более целесообразно использовать ЗD диаграммы размаха, которые вычисляют вариацию для выборок, представленных на графике).

Основное различие между диаграммами диапазонов и диаграммами размаха состоит в том, что на диаграммах диапазонов все значения, определяющие диапазоны («средние точки», минимум и максимум), не вычисляются по данным, а являются исходными значениями переменных.

Когда на графике нужно представить только одну переменную, обычно достаточно воспользоваться 2D диаграммой диапазонов; на этом графике также можно представить несколько переменных (путем сдвига изображений так, что для каждого наблюдения будет отображено последовательно столько диапазонов, сколько переменных используется для анализа). Тем не менее ЗD диаграмма диапазонов часто является более подходящим способом представления диапазонов нескольких переменных на одном графике, т. к. она не «разбивает» строки пиктограмм, представляющих отдельные классы или переменные.

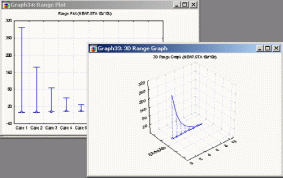
Рисунок 40. Пример трехмерной диаграммы диапазонов