Диаграммы времени

Показывают распределение данных в зависимости от времени.

Временная шкала (timeline). Показывает значения из набора данных на горизонтальной оси, которая соответствует времени. Отрезки между значениями могут быть любой величины. Например, линия годов XX века, на которой отмечены крупные военные конфликты.

Рисунок 27. Пример временной шкалы

Диаграмма Гантта (Gantt diagram). Показывает последовательность, длительность, а также время начала и окончания этапов и конкретных задач, необходимых для выполнения проекта. Отображается в виде “водопада” из одного или нескольких каскадов — соединенных стрелками блоков, выстроенных по диагонали сверху вниз, слева направо (т.е. «лестницей»). Причем длина блока зависит от необходимого для выполнения времени. Например, задачи, которые нужно выполнить для написания, подготовки к печати и выпуска книги. Диаграмму можно также отнести и к группе визуализирующих процесс, но обе ее части (длительность и последовательность действий) одинаково важны, поэтому тут уже дело вкуса.

Рисунок 28. Пример диаграммы Гантта

Диаграммы связей

Показывают связи внутри набора данных, как правило достаточно большого.

Круговая диаграмма связей (network diagram, arc diagram). Показывает связи внутри набора данных в виде кольца, на котором расставлены значения. Значения связаны дугами или линиями, находящимися во внутренней области круга. При большом количестве значений они могут находиться и внутри кольца, хотя это менее наглядно. Связи также могут иметь направление. Например, являются ли взаимными друзьями участники группы в социальной сети.

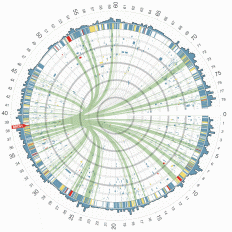
Рисунок 29. Пример круговой диаграммы связей

Линейная диаграмма связей. Показывает связи внутри набора данных в виде линии, на которой расставлены значения. Значения связаны дугами, находящимися сверху и снизу линии. Связи также могут иметь направление. Это альтернативный вариант отрисовки круговой диаграммы связей — смысл и задачи у них одинаковые.

Рисунок 30. Пример линейной диаграммы связей

Дендрограмма (dendrogram). Показывает близость значений набора данных по одному из параметров, используя ось Y для расстановки самих значений, а ось X — величины параметра. Отображается в виде набора соединяющихся друг с другом горизонтальных линий, которые соединяются, если значения совпадают по параметру. Причем чем раньше совпадение значений находится по оси X, тем ближе они друг к другу. Например, сравнение годовой выручки 30 предприятий.

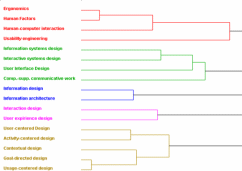
Рисунок 31. Пример дендограммы

Трехмерные модели визуализации

Трехмерный визуальный анализ позволяет анализировать данные в трехмерном пространстве, например, строить трехмерное изображение последовательностей исходных данных (наблюдений) для одной или нескольких выбранных переменных. Выбранные переменные представляются по оси Y, последовательные наблюдения — по оси X, а значения переменных (для данного наблюдения) откладываются по оси Z, как показано ниже.

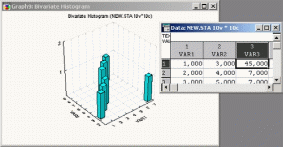
Рисунок 32. Пример трехмерного графика

Такие трехмерные графики используются для визуализации последовательностей значений нескольких переменных. По своей идее они сходны с составными линейными графиками, с тем лишь отличием, что для 3D диаграмм исходных данных ленты, линии, параллелепипеды и другие трехмерные представления значений каждой переменной не перекрываются (как на двухмерном графике), а «раздвигаются» в трехмерной перспективе.

ЗD диаграммы исходных данных применяются как для отображения данных, так и для аналитических исследований. Наиболее типичным приложением ЗD диаграмм исходных данных является наглядное представление имеющейся информации (например, о ценах, о росте населения, о взаимосвязи объемов продаж и прибыли). Такие графики позволяют просто и эффектно представить последовательности наблюдений, таких, например, как различные типы временных рядов.

Основное преимущество трехмерных представлений перед двухмерными составными линейными графиками заключается в том, что для некоторых множеств данных при объемном изображении легче распознавать отдельные последовательности значений. При выборе подходящего угла зрения с помощью, например, интерактивного вращения линии графика не будут перекрываться или «попадать друг на друга», как часто бывает на составных линейных двухмерных графиках.

Трехмерные диаграммы также используются в аналитических целях при исследовании входных данных, имеющих матричный формат.

Столбчатая диаграмма

Этот последовательный график представляет отдельные значения одной или нескольких серий данных по оси Х в виде серий трехмерных столбцов (параллелепипедов). Все серии отделены друг от друга промежутками вдоль оси Y. Высота каждого столбца по оси Z отвечает значению соответствующей точки данных.

Рисунок 33. Пример трехмерной столбчатой диаграммы

 

Блоковая диаграмма

Этот последовательный график представляет отдельные значения одной или нескольких серий данных по оси X в виде серий «трехмерных блоков». Все серии отделены друг от друга промежутками вдоль оси Y. Высота начала каждого блока по оси Z отвечает значению соответствующей точки данных.

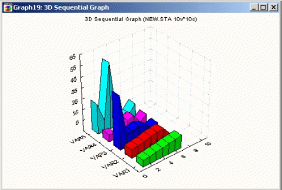
Рисунок 34. Пример трехмерной блочной диаграммы

Ленточная диаграмма

Эта диаграмма представляет отдельные значения одной или нескольких серий данных по оси X в виде серий «лент» в трехмерном пространстве.

Рисунок 35. Пример трехмерной ленточной диаграммы

Все серии отделены друг от друга промежутками вдоль оси Y. Высота начала каждой ленты по оси Z отвечает значению соответствующей точки данных.

Линейный график

Этот последовательный график представляет отдельные значения одной или нескольких серий данных по оси X в виде ряда непрерывных линий в трехмерном пространстве.

Рисунок 36. Пример трехмерного линейного графика

Все серии отделены друг от друга промежутками на оси Y. Высота начала каждой линии по оси Z отвечает значению соответствующей точки данных.

 

Диаграмма всплесков

Данный последовательный график представляет отдельные значения одного или нескольких наборов данных по оси Х в виде серий «всплесков» (точек с перпендикулярами, опущенными на плоскость основания).

Рисунок 37. Пример трехмерной диаграммы всплеска

Все серии отделены друг от друга промежутками вдоль оси Y. Высота каждого перпендикуляра по оси Z отвечает соответствующему значению серии.