3 . Швидкість і прискорення точки при векторному способі завдання руху.

Швидкістю точки називають векторну величину, що визначає інтенсивність зміни положення точки в просторі з часом.

Нехай у момент часу положення точки визначається радіусом-вектором (рис. 1.4), а в момент -радіусом-вектором . Вектор називають вектором переміщення точки за час .

Середньою швидкістю точки за проміжок часу називається векторна величина .

Очевидно, що напрямок вектора середньої швидкості збігається з напрямком вектора . У системі СИ одиницями виміру швидкості можуть бути м/сек, см/сек, км/годину. При рішенні практичних задач необхідно пам'ятати, що 1 м/сек = 3,6 км/годину.

Миттєвою швидкістю називається межа відносини вектора переміщення точки до відповідного проміжку часу , коли прагне до нуля. З цього визначення випливає , що миттєва швидкість точки дорівнює першій похідній від радіуса-вектора точки за часом

(1.4)

Вектор миттєвої швидкості завжди збігається з дотичною до траєкторії в заданому положенні точки і спрямований убік руху (рис. 1.4).

Прискоренням точки називають векторну величину, що визначає інтенсивність зміни швидкості точки з часом.

Якщо в момент часу швидкість точки – , а в момент часу – , то вектор = – називають вектором зміни швидкості точки за час .

Середнім прискоренням точки за проміжок часу називається векторна величина .

Очевидно, що напрямок вектора середнього прискорення збігається з напрямком вектора . У системі СИ одиницями виміру прискорення швидкості можуть бути м/сек², см/сек².

Миттєвим прискоренням називається межа відносини вектору зміни швидкості точки до проміжку часу , коли прагне до нуля. З цього визначення випливає, що миттєве прискорення точки дорівнює першій похідній від вектора швидкості за часом або другою похідною від радіуса-вектора за часом

(1.5)

П ри прямолінійному русі вектор спрямований вздовж прямій. Якщо траєкторією є плоска крива, то вектор прискорення лежить у площині траєкторії і спрямований убік її увігнутості. При цьому, якщо вектор швидкості утворить з вектором прискорення гострий кут (рис. 1.5), то рух точки називають прискореним, якщо – тупий кут (рис. 1.6), то рух точки називають уповільненим.

4. Швидкість і прискорення точки при координатному способі завдання руху

Вектор швидкості може бути записаний через його проекції на осі декартової системи координат . При координатному способі завдання руху (1.2) на підставі виразу (1.4) легко отримати правило: проекції швидкості на координатні осі дорівнюють першим похідним від відповідних координат за часом

, , , ( 1.6 )

тут точка позначає диференціювання за часом

Геометрично вектор швидкості є діагоналлю паралелепіпеда, побудованого на складових вектора швидкості , , як на сторонах. При цьому модуль швидкості точки визначається по формулі:

( 1.7 )

Я кщо точка рухається в площині, то вектор швидкості – діагональ прямокутника, сторонами якого є (рис. .7). Завжди варто пам'ятати, що отриманий у такий спосіб вектор швидкості повинний збігатися з дотичної, проведеної до траєкторії в даному положенні точки М, що рухається.

Вектор прискорення може бути записаний через його проекції на осі декартової системи координат . При координатному способі завдання руху (1.2) на підставі виразу (1.5) легко отримати правило: проекції прискорення на координатні осі дорівнюють першим похідним від відповідних проекцій швидкості , , за часом або другим похідним від відповідних координат за часом

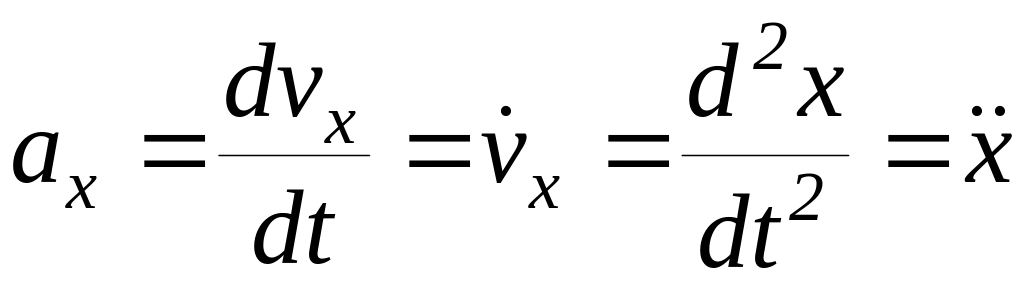, , , ( 1.8 )

тут дві точки позначають другу похідну за часом.

Г еометрично вектор прискорення є діагоналлю паралелепіпеда, побудованого на складового вектора прискорення , , . як на сторонах. При цьому модуль прискорення точки визначається по формулі:

. (1.9)

Якщо точка рухається в площині, то вектор прискорення - діагональ прямокутника, сторонами якого є , (Рис. 8). Завжди варто пам'ятати, що отриманий у такий спосіб вектор прискорення повинний бути спрямований убік увігнутості траєкторії точки.