МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

“ КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ “

РОБОТА № 2-3

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ТЕПЛОВІДДАЧІ ЗА УМОВ

ВИМУШЕНОГО РУХУ ПОВІТРЯ УСЕРЕДИНІ

ГОРИЗОНТАЛЬНОЇ ТРУБКИ

КИЇВ НТУУ “КПІ“ 2011

1. Постановка завдання

Метою лабораторної роботи є поглиблення знань з теорїї тепловіддачі за умов вимушеної конвекції усередині горизонтальної трубки, дослідне визначення середніх коефіцієнтів тепловіддачі, ознайомлення із методикою експериментального дослідження процесу, а також набуття навичок у проведенні експерименту і узагальненні отриманих даних, оцінка похибок експерименту, порівняння отриманих результатів із розрахунковими.

У результаті виконання роботи повинні бути засвоєні поняття конвективного теплообміну, вимушеної конвекції, конвективної тепловіддачі та коефіцієнта тепловіддачі. Також потрібно з`ясувати характер зміни коефіцієнтів тепловіддачі за умов вимушеної конвекції в залежності від швидкості потоку та інших супутних факторів, які обумовлюють процес вимушеної конвекції.

У цій лабораторній роботі необхідно:

1. Експериментально визначити значення середніх коефіцієнтів тепловіддачі для умов вимушеного руху повітря усередині горизонтальної трубки, а також встановити його залежність від швидкості потоку.

2. Для умов експерименту визначити значення коефіцієнтів тепловіддачі за узагальненою формулою у вигляді рівняння подібності та порівняти їх із дослідними величинами.

3. Перевірити розрахунками баланс за тепловими потоками, які виділяються електричним нагрівачем та сприймаються вимушеним потоком повітря усередині горизонтальної трубки; визначити імовірні причини можливих розбіжностей.

До виконання лабораторної роботи слід приступати після ознайомлення із запропонованою інструкцією, а також літературними джерелами [1-4].

2. Теоретичні відомості

Конвективною тепловіддачею називають процес конвективного теплообміну між поверхнею твердого тіла та рідиною, яка її омиває.

Розрахунок кількості теплоти, що передається за умов конвективної тепловіддачі, виконується за допомогою закону Ньютона-Ріхмана, який для щільності теплового потоку має вигляд, Вт/м²:

, (1)

де a - коефіцієнт тепловіддачі, Вт/(м².⁰С),

Dt - температурний натиск між стінкою t_C та рідиною. яка її омиває t₀: якщо t_C > t₀, то Dt = t_C - t₀, а якщо t_C < t₀, то Dt = t₀ - t_C.

Простий математичний запис рівняння (1) має досить складну величину коефіцієнта тепловіддачі. Із цією величиною пов`язані усі складності розрахунку конвективного теплообміну. Як свідчить досвід, конвективна тепловіддача - це досить складний процес, який залежить від багатьох факторів. Наприклад, від природи виникнення руху рідини, режиму її течії, теплофізичних властивостей рідини, розмірів, форми та орієнтації поверхні теплообміну у просторі.

В залежності від природи виникнення руху рідини розрізняють природну та вимушену конвекцію.

Природна конвекція пов`язана із вільним гравітаційним рухом рідини, про що детальніше сказано у методичних вказівках до лабораторних робіт:

2-1 Тепловіддача горизонтальної трубки за умов природної конвекції (вільний рух повітря);

2-2 Тепловіддача вертикальної трубки за умов вільного руху повітря (природна конвекція).

Вимушений рух рідини виникає під дією зовнішніх збудників руху, таких як вентилятор, компресор, насос та ін.

Досліди вказують на те, що інтенсивність теплообміну за умов вимушеного руху значно вища ніж для природної конвекції, якщо інші умови для цих процесів будуть однаковими.

Для неізотермічної течії вимушений рух рідини може супроводжуватися також і її вільним рухом. За досить великих швидкостей вимушеного руху рідини природною конвекцією нехтують.

У гідродинаміці розрізняють ламінарний, перехідний та турбулентний режими течії. Гідродинаміка процесу вимушеної конвекції характеризується числом Рейнольдса, яке вказує на співвідношення сил інерції та в`язкості у потоці рідини:

, (2)

де W - швидкість потоку рідини, м/с;

l₀ - визначальний характерний лінійний розмір, який у випадку круглої труби дорівнює її геометричному діаметру, м;

n - коефіцієнт кінематичної в`язкості рідини, м²/с.

Як гідродинаміка, так і теплообмін рухомої рідини у трубах та каналах досить складні. Це пов`язано із тим, що поперечний періз каналів має кінцеві розміри. Тому на певній відстані від входу у трубку сили тертя розповсюджуються на усю масу рідини. Внаслідок цього температура рідини змінюється як у напрямку руху рідини, так і у поперечному напрямку.

В залежності від режиму течії розрізняють і відповідні їм режими тепловіддачі:

- ламінарний режим;

- перехідний режим;

- турбулентний режим.

Для числа Рейнольдса визначальна температура - це середня температура рідини при проходженні через канал, ⁰С:

. (3)

Для ламінарного режиму течії в трубах розрізняють в`язкісний та в`язкісно-гравітаційний підрежими течії. Визначення підрежиму течії ведеться для середньої температури між стінкою трубки t_C та рідиною t₀, ⁰С:

, (4)

за добутком чисел Грасгофа Gr та Прандтля Pr:

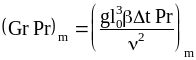, (5)

де l₀ - визначальний розмір, м;

g - прискорення вільного падіння (земного тяжіння), м/с²;

Dt - різниця температур між стінкою та рідиною, ⁰С;

n - коефіцієнт кінематичної в`язкості, м²/с;

b - коефіцієнт об`ємного розширення, К^-1.

Для формули (5) теплофізичні властивості рідини обираються із відповідних таблиць за визначальною температурою t=t_m.

Для газового середовища (некраплинної рідини), яке за своїми властивостями близьке до ідеального термодинамічного газу, коефіцієнт об`ємного розширення може бути розрахований так, К^-1:

, (6)

де T= t + 273 - визначальна температура, К.

Якщо добуток (5) складає менше, ніж 8^.10⁵ , то режим течії буде в`язкісним. Розрахунок середньої тепловіддачі цього процесу ведуть із застосуванням емпіричного рівняння подібності за визначальної температури t_m:

, (7)

де d - діаметр каналу - визначальний розмір, м;

L - довжина каналу, м;

m - коефіцієнт динамічної в`язкості: із індексом “с” обирається для рідини за температурою стінки t_C, а без індексу - за середньою температурою рідини t₀ (див. формулу 3) , Па . с;

- число Нусельта,

- число Пекле, яке дорівнює добутку чисел Рейнольдса та Прандтля , де - коефіцієнт температуропровідності, м²/с;

e - поправка, яка пов`язана із початковою дільницею стабілізації потоку рідини.

Формула (7) перевірена для

(m_С/m)=0,07...1.500 та . (8)

Поправка на початкову дільницю формування гідродинамічного та теплового граничних пластів має вигляд:

, (9)

де визначальна температура - це середня температура потоку рідини t=t₀ (див. формулу 3).

Рівняння (9) застосовується за такої умови:

. (10)

Якщо добуток , то для розрахунку тепловіддачі для в`язкісно-гравітаційного режиму течії застосовується емпіричне рівняння подібності:

, (11)

де визначальна температура дорівнює середній температурі потоку рідини t=t₀ (формула 3), а поправка на початкову термічну дільницю стабілізації потоку визначається [1] за таблицею 8.1, якщо виконується умова (L/d) < 50. Вибіркові дані для цього випадку наведені у табл. 1:

Таблиця 1

Поправка e для ламінарної в`язкісно-гравітаційної течії рідини

L/d	e	L/d	e	L/d	e
1	1,90	10	1,28	30	1,05
2	1,70	15	1,18	40	1,02
5	1,44	20	1,13	50	1,00

Для розрахунку середньої тепловіддачі в умовах перехідного режиму течії рідини застосовується узагальнене рівняння:

. (12)

Для розрахунку середньої тепловіддачі в умовах турбулентного режиму течії застосовується рівняння подібності, отримане М.А.Міхеєвим:

, (13)

де e_L - поправка на початкову дільницю - визначається [3] за таблицею на с.84;

e_R - емпірична поправка, яка пов`язана із кривизною каналу (трубки):

, (14)

де R - радіус кривизни, м. Якщо трубка пряма, то e_R = 1.

Крім того, для розрахунку середньої тепловіддачі у випадку турбулентної течії газового теплоносія усередині круглої трубки за умови Pr » 1 застосовується рівняння подібності:

. (15)

У випадку повітря емпіричне рівняння подібності (15) матиме вигляд:

. (16)

Коефіцієнт тепловіддачі, знайдений через число Нусельта за допомогою емпіричних рівнянь подібності, слід підставити в закон Ньютона-Ріхмана для визначення теплового потоку, Вт:

, (17)

де F = pdL - площа поверхні теплообміну - внутрішньої поверхні трубки (канала), м².

Примітка. Перевагу у розрахунках слід віддавати рівнянням подібності, які найбільш точно відповідають умовам даного експерименту.