2. Геометрическое решение злп
Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения.
Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования.
Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.
1. Сформулировать ЗЛП.
2.
Построить на плоскости
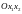прямые, уравнения которых получаются
в результате замены в ограничениях
знаков неравенств на знаки точных
равенств.
3. Найти полуплоскости, определяемые каждым из ограничений задачи.
4. Найти область допустимых решений.
5.
Построить прямую
,
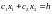где
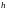– любое положительное число, желательно
такое, чтобы проведенная прямая проходила
через многоугольник решений.
6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.
7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.
Далее рассмотрим решение примера 1 графическим методом.
Выше уже приводилась формулировка задачи, здесь нам остается лишь повторить ее:
при ограничениях по ресурсам
и ограничениях неотрицательности
, .
2. Теперь построим прямые, соответствующие каждому из функциональных ограничений задачи (см. рисунок 1). Эти прямые обозначены на рисунке (1), (2) и (3).
(3)
(2)
(1)
A
B
f(x)=0
C
O D
Рисунок 1 - Геометрическое решение ЗЛП
3. Область допустимых решений включает в себя точки, для которых выполняются все ограничения задачи. В нашем случае область представляет собой пятиугольник (на рисунке обозначен OABCD).
5. Прямая, соответствующая целевой функции, на рисунке представлена жирной линией. Оказывается, что если оптимальный план существует, то он обязательно будет лежать в одной из угловых точек множества допустимых планов, т. е. в одной из вершин OABCD.
Можно, в принципе, не перебирать все угловые точки множествадопустимых решений. Для этого удобно воспользоваться понятием градиента:
градиент
функции
– это вектор, координаты которого равны
частным производным функции по
соответствующим переменным:
.
Градиент функции , вычисленный в некоторой точке, перпендикулярен линии уровня функции, проходящей через эту точку, и показывает направление наибольшего роста функции в этой точке.
Градиент
функции выручки
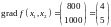
указывает
направление наибольшего возрастания
функции
.
Линии уровня функции образуют семейство параллельных прямых, перпендикулярных градиенту.
6. Будем двигать линию уровня в направлении градиента параллельно самой себе вверх (направление указано стрелкой), поскольку именно при движении в этом направлении значение целевой функции увеличивается. Последней точкой многоугольника решений, с которой соприкоснется передвигаемая прямая, прежде чем покинет его, является точка B. Это и есть точка, соответствующая оптимальному решению задачи.
7.
Осталось вычислить координаты точки
B.
Она является точкой пересечения прямых
(1) и (2). Решив совместно систему уравнении
этих прямых
,
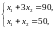найдем координаты точки B:
B(30,
20). Подставляя найденные величины в
целевую функцию, найдем ее значение в
оптимальной точке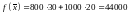 
.
Таким образом, для максимизации прибыли предприятию следует ежедневно выпускать 30 изделий A и 20 изделий Б. Реализация такого плана обеспечит ежедневную прибыль в размере 44000 ден.ед.
Данную задачу мы смогли решить графическим способом, поскольку рассматриваемое предприятие выпускает всего два наименования продукции. Ассортимент продукции, выпускаемой реальными предприятиями гораздо шире, и для оптимизации деятельности таких предприятий графическим методом не обойтись.
Решая задачу линейного программирования графическим способом, мы можем встретиться со следующими случаями:
а б
в г
Рисунок 2
На рис. 2, а изображен случай, когда целевая функция имеет единственную точку максимума – точку А и единственную точку минимума – точку О. В случае б максимума у целевой функции нет, так как она может неограниченно возрастать. Точек минимума в случае б бесконечно много. Все точки отрезка СK будут точками минимума. В случае в целевая функция имеет единственную точку максимума и не имеет минимума (не ограничена снизу). В случае г область допустимых планов пустая. Решений нет.