МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НАБЕРЕЖНОЧЕЛНИНСКИЙ ИНСТИТУТ (ФИЛИАЛ) ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Кафедра «Математические методы в экономике»
Лабораторная работа №4
Сетевое планирование
Вариант №1
Выполнила:
Проверила:
Набережные Челны 2013 г
Содержание
Задание
I. Проверка соответствия сетевого графика требованиям построения
II. Упорядочение сетевого графика
III. Расчет критического пути сетевого графика
IV. Временные характеристики сетевого графика
V. Оптимизация сетевого графика по схеме «время - стоимость»
VI. Коэффициент напряженности работы
VI. Сетевое планирование в условиях неопределенности
Выводы
Задание
Лабораторная работа №4
Цель работы: изучить методы сетевого планирования и управления
Исходные данные:
Вариант №1
Предположим, что при составлении некоторого проекта выделено 9 событий и 16, связывающие их работы. На основе выделенных событий и работ составлен сетевой график.
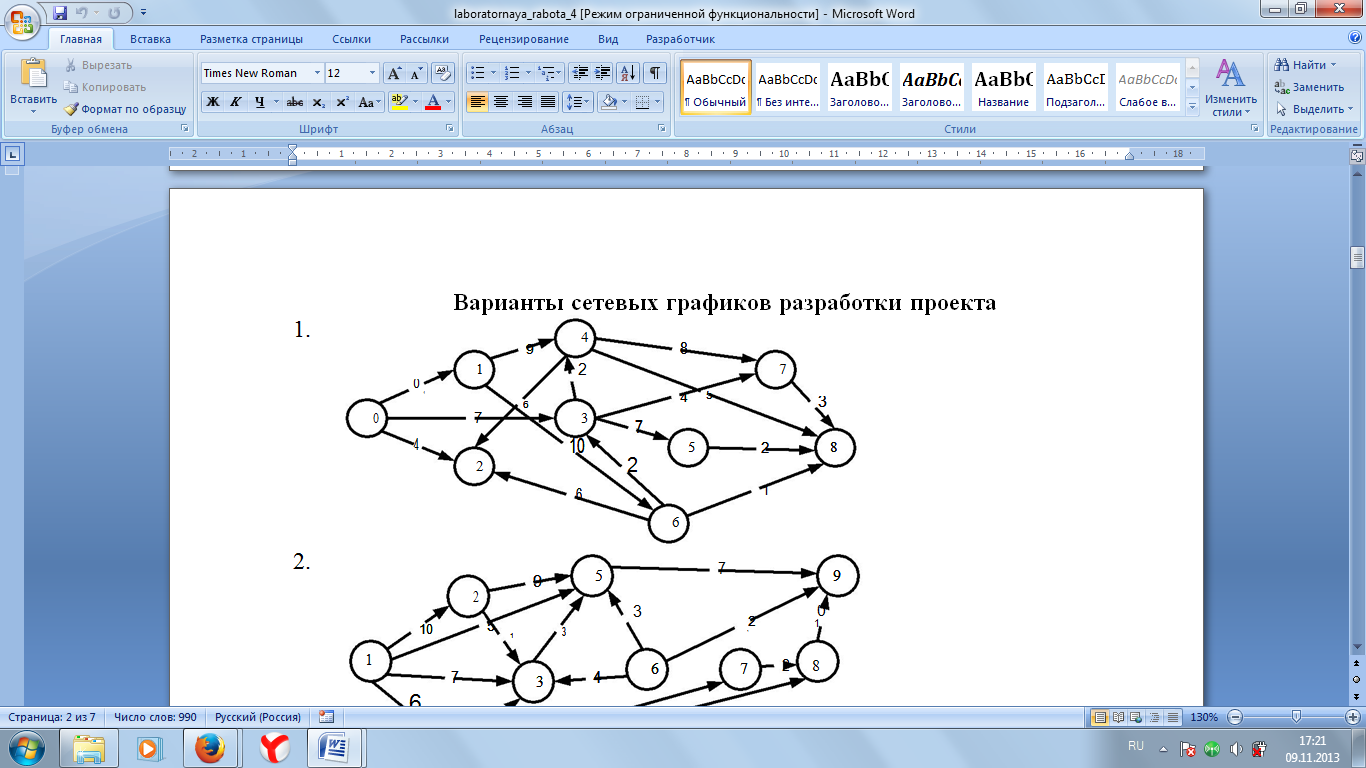
Рис. 1 Сетевой график
I. Проверка соответствия сетевого графика требованиям построения
В представленном сетевом графике (рисунок 1) нет «тупиковых» и «хвостовых» событий, отсутствуют замкнутые контуры. Но на сетевом графике имеется 2 конечных (завершающих) события (событие 2 и 8). Для исключения подобной ситуации, необходимо ввести дополнительную (фиктивную) работу (2,9 и 8,9) с нулевым значением (t = 0, событие 9).
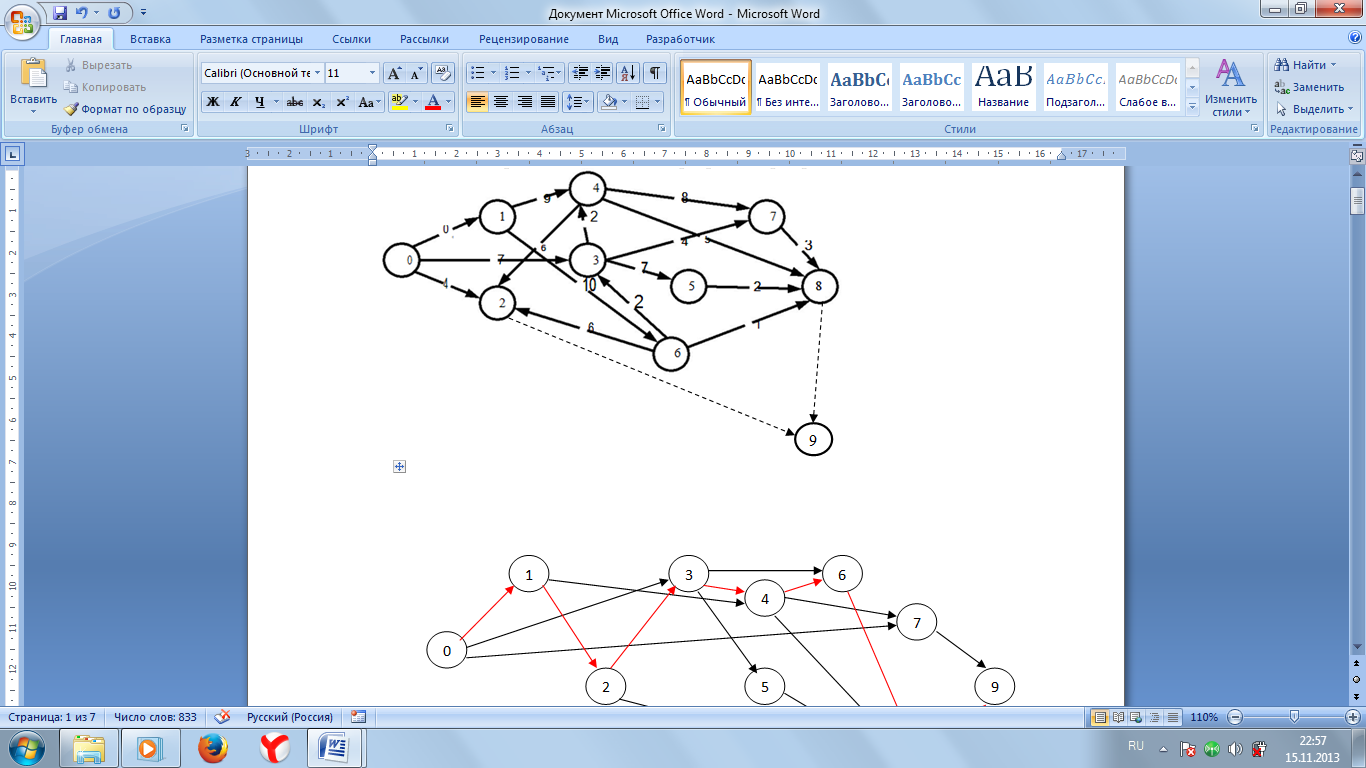
Теперь сетевой граф имеет одно исходное и одно завершающее события. Исходным событием сетевого графика является событие 0 (ему не предшествуют никакие работы), а завершающим – событие 9 (за ним не следует ни одна работа). График удовлетворяет всем правилам построения сетевых графов, однако он не полностью упорядочен.
II. Упорядочение сетевого графика
Упорядочение сетевого графика заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием
Данный сетевой график не является полностью упорядоченным. Выполним его упорядочение, для чего условно разобьем сетевой график на несколько вертикальных слоев. Полагая на сетевых графиках изменение времени слева на право, поместим событие 0 в левую часть графика, а событие 9 – в правую часть, разместив между ними промежуточные события в некотором порядке, соответствующим их номерам.
Упорядочение осуществляется следующим образом:
На первом слое размещается единственное начальное событие 0.
На втором слое размещается событие 1, исходящее из начального события 0 и не имеющее входящих работ.
На третьем слое размещается событие 6, исходящее из 1-го события и не имеющее входящих работ.
На четвертом слое размещается событие 3, исходящее из 0-го и 6-го событий и не имеющее входящих работ.
На пятом слое размещается событие 4, исходящее из 1-го и 3-го события, и событие 5, исходящее из 3-го события, не имеющие входящих работ.
На шестом слое размещается событие 7, исходящее из 3-го и 4-го события и не имеющее входящих работ.
На седьмом слое размещаются событие 2, исходящее из 0-го и 4-го события, и событие 8, исходящее из 4-го, 5-го, 6-го и 7-го событий, и не имеющие входящих работ.
На восьмом слое размещается событие 9, исходящее из 2-го и 8-го события, и не имеющие входящих работ.
В результате получим рисунок 2.
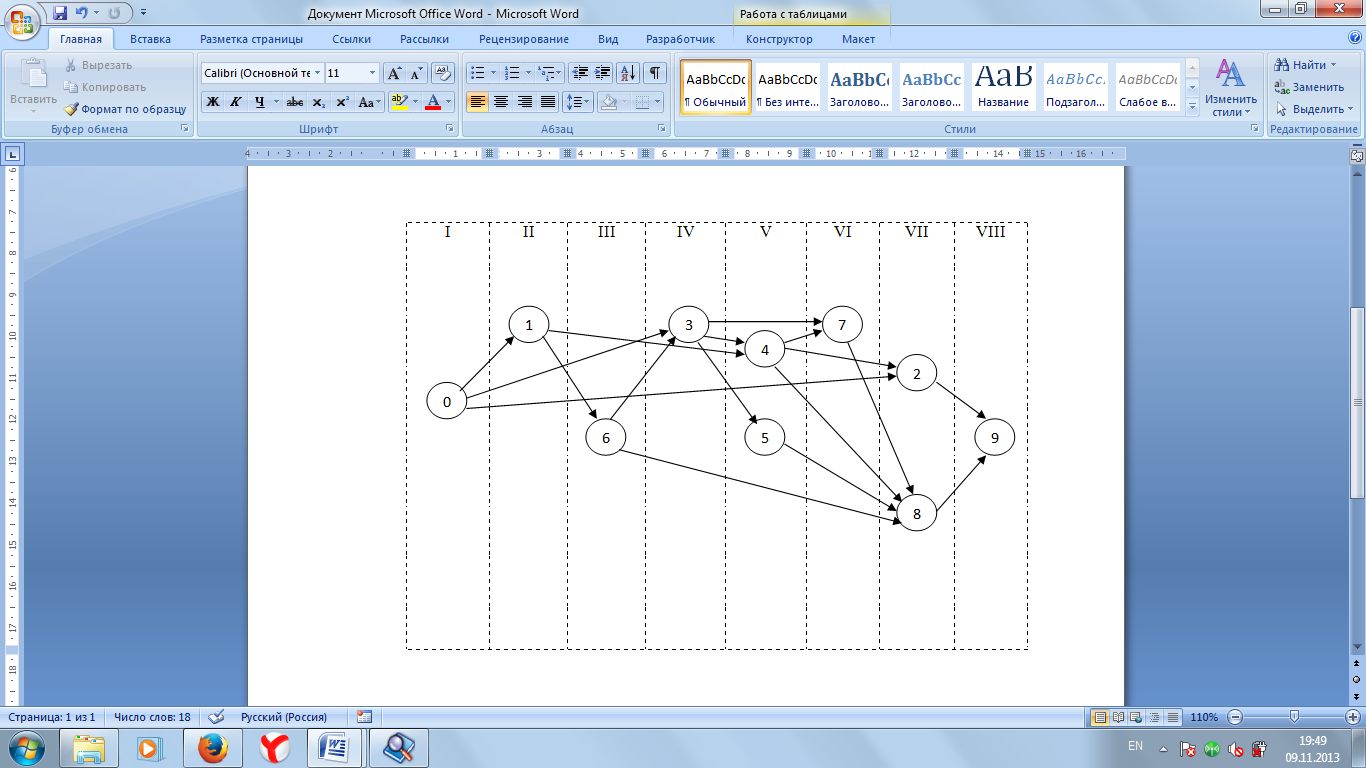
Рис. 2 - Сетевой график с разбивкой по слоям
Данный график требует изменения нумерации, так как изначальная нумерация событий не совсем правильная: так событие 3 лежит в IV слое и имеет номер меньший, чем событие 6 из предыдущего слоя, тоже можно сказать о событии 2.
Таким образом, мы получили упорядоченный сетевой график.
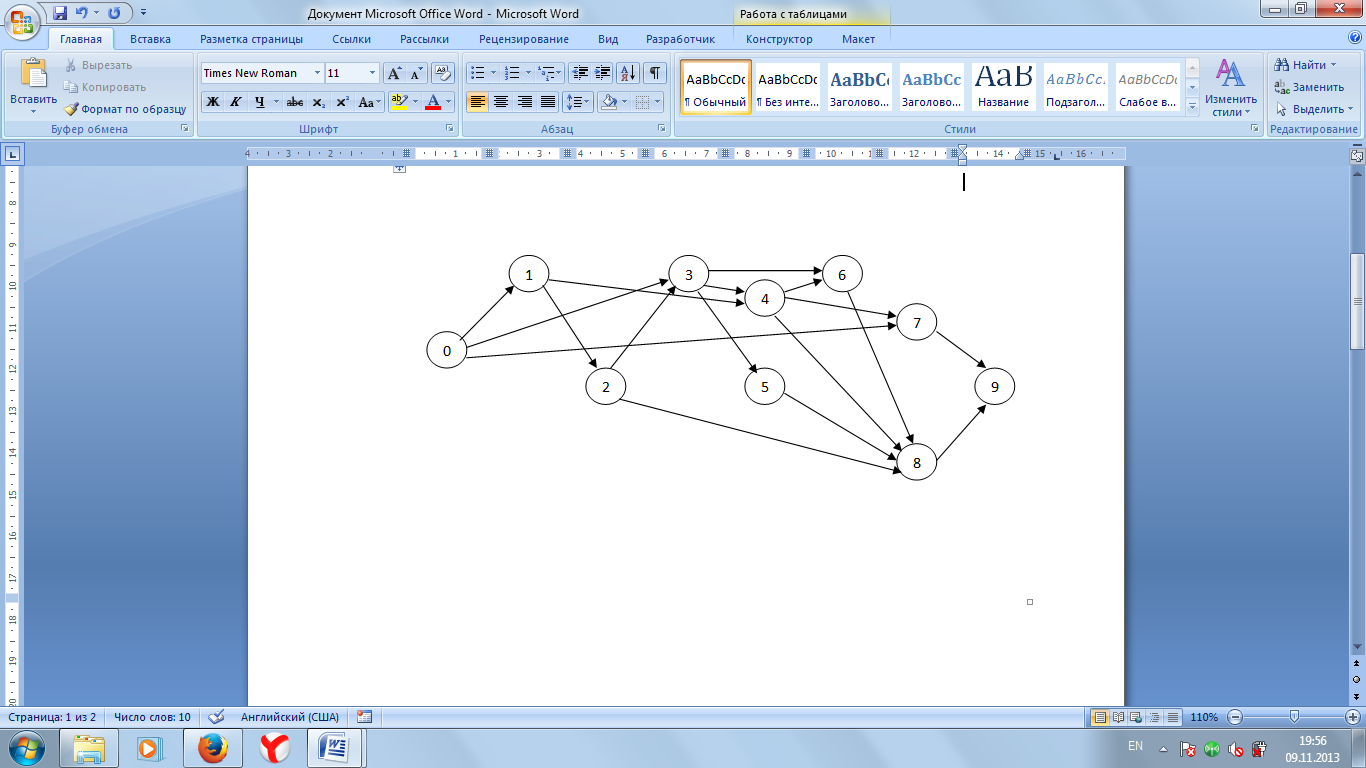
Таблица 1 – Исходные данные для расчета параметров сетевого графика1
№ |
Работы t(i,j) |
Продолжительность работ, сутки |
Стоимость работы, условные руб. |
||||
п/п |
i |
j |
a(i,j) |
t(i,j) |
b(i,j) |
Cmin(i,j) |
Cmax(i,j) |
1 |
0 |
1 |
9 |
10 |
18 |
60000 |
96000 |
2 |
0 |
3 |
5 |
7 |
15 |
1000 |
4300 |
3 |
0 |
7 |
2 |
4 |
26 |
65000 |
95000 |
4 |
1 |
2 |
5 |
6 |
10 |
1500 |
6500 |
5 |
1 |
4 |
6 |
9 |
10 |
12000 |
18000 |
6 |
2 |
3 |
1 |
2 |
3 |
5000 |
10000 |
7 |
2 |
8 |
1 |
1 |
21 |
500 |
1500 |
8 |
3 |
4 |
1 |
2 |
8 |
7000 |
21000 |
9 |
3 |
5 |
4 |
7 |
12 |
5500 |
11500 |
10 |
3 |
6 |
3 |
4 |
6 |
30000 |
90000 |
11 |
4 |
6 |
7 |
8 |
9 |
3000 |
7000 |
12 |
4 |
7 |
5 |
6 |
17 |
16000 |
40000 |
13 |
4 |
8 |
3 |
5 |
7 |
25000 |
8500 |
14 |
5 |
8 |
1 |
2 |
4 |
55000 |
175000 |
15 |
6 |
8 |
1 |
3 |
6 |
25000 |
55000 |
16 |
7 |
9 |
0 |
0 |
0 |
0 |
0 |
17 |
8 |
9 |
0 |
0 |
0 |
0 |
0 |
1Примечание:
t(i, j) – продолжительность работ;
a(i, j) – минимальная продолжительность работ;
b(i, j) – максимальная продолжительность работ;
задаются самостоятельно
Cmin (i, j) – минимальная стоимость работ;
Cmax (i, j) – максимальная стоимость работ.