
- •Матрицы.
- •Умножение матрицы на число и сложение матриц.
- •Умножение матриц.
- •Определители квадратных матриц.
- •Определители третьего порядка.
- •Определители n-ного порядка.
- •Разложение определителя по строке или столбцу.
- •Свойства определителей n-ого порядка.
- •Понятие минора. Вычисление определителей n-ого порядка.
- •Связь между минорами и алгебраическими дополнениями.
- •Обратная матрица.
- •Транспонирование матрицы.
- •Нахождение обратной матрицы а-1 в случае невырожденной матрицы а.
- •Умножение матрицы на вектор.
- •Матрично-векторная форма записи системы линейных уравнений.
- •Запись решения с помощью обратной матрицы.
Матрично-векторная форма записи системы линейных уравнений.
Рассмотрим систему линейных уравнений

и введём следующие обозначения:
А
=
, х =
 , В =
, В =
 .
.
Матрицу А называют матрицей системы линейных уравнений, х –вектор – столбец неизвестных, а В–вектор-столбец свободных членов.
Т.к. столбцов у матрицы А ровно столько, сколько координат у вектора-столбца х, то определено произведение
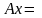

Теперь систему линейных уравнений можно записать в виде одного векторного равенства Ах = В.(1)
Запись решения с помощью обратной матрицы.
Особое значение имеют системы с одинаковым числом уравнений и неизвестных – системы n n. В этом случае матрица А является квадратной матрицей размера n n. Допустим, что эта матрица невырожденная, т.е. что её определитель не равен 0. Тогда для неё существует обратная матрица А-1.
Используя эту матрицу, можно решить уравнение (2): умножая обе части уравнения (2) слева на матрицу А-1, получаем
А-1(Ах) = А-1В
или, согласно сочетательному закону умножения матриц,
(А-1А)х = А-1В.
Но А-1А = Е, а Ех = х. Уравнение принимает вид
х = А-1В.
Эта формула даёт матричную запись решения.
Замечание. Не следует думать, что эта формула сильно упрощает задачу решения системы размера n n с невырожденной матрицей А. Ведь для того чтобы использовать эту формулу. Нужно сначала найти матрицу А-1, а это само по себе есть достаточно трудная задача. Поэтому формула имеет скорее теоретическое значение. Наиболее удобным способом остаётся метод Гаусса.
Пример. Решить систему уравнений
 х1
+ 3х3 = 1
х1
+ 3х3 = 1
5х1 + 3х2 + 7х3 = 1
3х1 + 2х2 + 5х3 = 1.
А
=
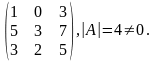
Вычислим матрицу А-1:
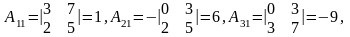
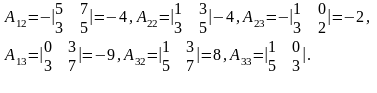
А-1
=
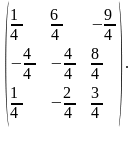
Теперь находим столбец х:
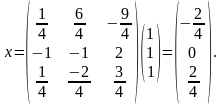
Итак,
решение системы:х1 = -
