Связь между минорами и алгебраическими дополнениями.

Теорема. Алгебраическое дополнение любого элемента a_ij определителя равно минору этого элемента. Умноженному на (-1)^i+j, т.е.

A_ij = (-1)^i+jM_ij.

Иначе говоря, всегда справедливо одно из равенств A_ij = 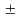M_ij, причём знак + имеет место в случае, когда сумма i+j чётная, и знак – в случае, когда указанная сумма нечётная.

Пример. Вычислить определитель четвёртого порядка

Обратная матрица.

Квадратная матрица

называется единичной и обозначается через Е.

Легко проверить, что какова бы ни была матрица А

АЕ = ЕА = А.

Определение. Квадратную матрицу А называют невырожденной, если её определитель не равен 0:

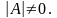
Квадратная матрица А называется обратимой, если можно подобрать такую матрицу В, что АВ = ВА = Е.

Матрица В называется обратной для матрицы А.

Обратимая матрица имеет только одну обратную матрицу, которую обозначают через А^-1. Т.о. АА^-1 =Е, А^-1А = Е.

Для вырожденной матрицы не существует обратной.

Свойства обратной матрицы.

( А^-1)^-1 = А, (АВ)^-1 = В^-1А^-1.

Транспонирование матрицы.

Наряду с матрицей А часто приходится рассматривать матрицу, столбцами которой являются строки матрицы А. Эту матрицу называют транспонированной к А и обозначают через А´ или А^т.

Пример. Транспонированной к матрице

А =

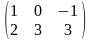
является матрица

А^т = .

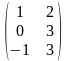Свойства операции транспонирования(k – число).

1.(Аk)^Т = kA^т.

2.(А+В) ^т = А^т + В^т.

3.(АВ)^т = В^тА^т.

4.(А^т)^т = А.

Нахождение обратной матрицы а-1 в случае невырожденной матрицы а.

Пусть А = - невырожденная матрица, т.е.

Теорема. Если А – невырожденная матрица, то

А^-1 =

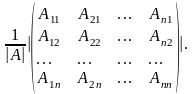
Здесь А_ij – алгебраическое дополнение для элемента а_ij .

Обратим внимание на своеобразное расположение чисел А_ij в матрице А^-1, а именно: число А_ij расположено не в i – той строке и j – том столбце, а, наоборот, в j – той строке и i– том столбце.

Доказательство.

Следует проверить справедливость равенств АА^-1 = Е и А^-1а = Е. Сделаем это для произведения АА^-1. Полагая АА^-1 = С, запишем

С = АА^-1 = · .

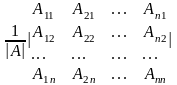Согласно правилу умножения матриц, элемент матрицы С, расположенный в i – той строке и j – том столбце, равен

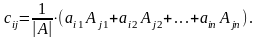
При i = j это выражение равно 1, т.к. тогда в скобках стоит разложение определителя по i – той строке; если же 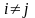, то написанное выражение равно 0, поскольку в этом случае в скобках стоит сумма произведений элементов i – той строки на алгебраические дополнения к соответствующим элементам j – той строки . Т.о., с_ij равно 1, если i = j , и равно 0, если . Это означает, что С = Е.

Пример 1.Найти обратную матрицу для матрицы

А = .

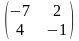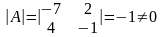; следовательно, матрица А^-1 существует. Чтобы записать её, находим числа А₁₁ = -1, А₁₂ = -4,А₂₁ = -2, А₂₂ = -7.

А^-1 = -

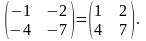
Пример 2.То же самое для матрицы

А =

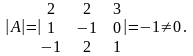
А₁₁ = А^-1 = -

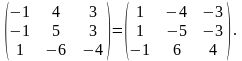
Умножение матрицы на вектор.

Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу – вектор-строкой.

Если А – матрица размера m × n, вектор-столбец х имеет размерность n , а вектор-строка y – размерность m, то определены произведения Ах и уА, причём Ах – вектор-столбец размерности m, а уА – вектор-строка размерности m.

Пример. Даны матрица А и векторы х и у:

А = 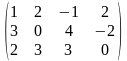, х = , у = (2, 1, -3).

Вычислить координаты векторов Ах и уА.

Имеем

Ах =

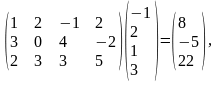
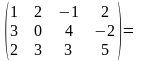уА = (2, 1, -3) (-1, -5, -7, -13).