Разложение определителя по строке или столбцу.

Предыдущая формула мало пригодна для вычисления определителей n-ого порядка: число членов равно n! И с ростом n это число быстро возрастает.

Практическое вычисление определителей основано в первую очередь на формулах разложения определителя по строке (столбцу).

Рассмотрим определитель n-ого порядка

.

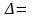Пусть i - одно из чисел 1, 2, …, n. Каждый член определителя содержит в качестве множителя один элемент i – той строки. Объединим все члены, содержащие a_i1 (первый элемент i – той строки), вынесем общий множитель a_i1 за скобки и выражение, оставшееся в скобках, обозначим A_i1. Далее объединим все члены, содержащие a_i2( их сумма a_i2A_i2), и т.д..

В результате сумма (4) распадётся на n частей:

a_i1A_i1, a_i2A_i2, …, a_inA_in.

Следовательно,

a_i1A_i1 + a_i2A_i2+ …+ a_inA_in. (5)

Это равенство называют разложением определителя по элементам i-той строки ( или просто по i-той строке). Выражение Aij называют при этом алгебраическим дополнением элемента a_ij в определителе .

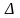Итак, определитель равен сумме произведений элементов любой строки на их алгебраические дополнения.

По аналогии с разложением определителя по строке записывается разложение определителя по столбцу.

Формулу (5) можно использовать для вычисления определителя . Однако для этого нужно уметь находить алгебраические дополнения. Для этого установим некоторые свойства определителей n-ого порядка.

Свойства определителей n-ого порядка.

Определитель не изменится, если поменять местами строки и столбцы.

Поэтому приводимые ниже свойства определителей формулируются для строк, для столбцов свойства аналогичны.

1.Если какая-либо строка определителя состоит из нулей, то и сам определитель равен 0.

Для доказательства достаточно разложить определитель по элементам данной строки.

2. При перестановке двух строк определитель умножается на –1.

3. Определитель, содержащий две одинаковые строки равен 0.

4. Общий множитель элементов любой строки можно выносить за знак определителя.

= k .

2. Если каждый элемент некоторой строки представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, в каждом из которых все элементы те же, что и в исходном определителе, за исключением элементов указанной строки. В первом определителе указанная строка состоит из первых слагаемых, во втором – из вторых. Например,

= + .

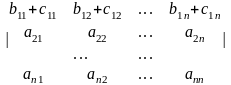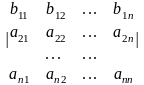2. Определитель не изменится, если к элементам некоторой строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число. Например,

= .

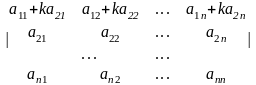7. Сумма произведений элементов какой-либо строки определителя на алгебраические дополнения к соответственным элементам другой строки равна 0. Например, а₂₁А₁₁ + а₂₂А₁₂ + … + а_2nA_{1 n} =0.

Пример. Вычислить определитель

= .

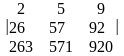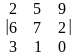Понятие минора. Вычисление определителей n-ого порядка.

Рассмотрим определитель n-ого порядка

= .

Выделим некоторый элемент a_ij.Если вычеркнуть из определителя

i-тую строку и j–тый столбец (т.е. строку и столбец, в которых расположен элемент a_ij), то останется некоторый определитель порядка n – 1. Его называют минором элемента a_ij. и обозначают М_ij. Например, в определителе четвёртого порядка

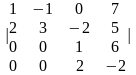
минор элемента а₂₃ = -2 равен

М₂₃ =