Определители квадратных матриц.

Определители второго порядка. Правило Крамера.

Пусть дана квадратная таблица, состоящая из четырёх чисел:

.

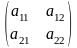Такие таблицы называют матрицами размера 2 2 или квадратными матрицами второго порядка.

Определение. Определителем матрицы второго порядка называют число

а₁₁a₂₂ – a ₁₂a ₂₁.

Определитель обозначают символом

det A = .

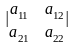Т.о., det A = = а₁₁a₂₂ – a ₁₂a ₂₁.

Пример.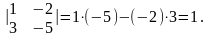

Следует различать матрицу и её определитель: матрица есть таблица из четырёх чисел, в то время как определитель – это единственное число, построенное указанным выше способом по данной таблице.

Числа а₁₁, а₁₂, а₂₁, а₂₂ называют элементами матрицы. Матрица имеет две строки и два столбца. Те же самые понятия элементов, строк и столбцов относятся и к определителю.

Хотя выражение для определителя несложно, всё же полезно запомнить следующую схему для его вычисления:

Определители третьего порядка.

Рассмотрим теперь квадратную матрицу третьего порядка, т.е. таблицу чисел

.

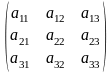Понятия элемента, строки, столбца вводятся для матрицы совершенно так же, как для матриц второго порядка.

Определение. Определителем матрицы называется число

а₁₁а₂₂а₃₃ + а₁₂а₂₃а₃₁ + а₁₃а₂₁а₃₂ – а₁₃а₂₂а₃₁ – а₁₂а₂₁а₃₃ – а₁₁а₂₃а₃₂.

Определитель записывают в виде

.

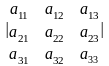Формулу, несмотря на внешнюю сложность нетрудно запомнить.

Из указанных схем вытекает простое правило вычисления определителя третьего порядка, которое называется правилом треугольника.

Пример. Вычислить определитель третьего порядка

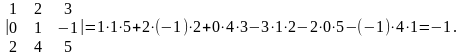
Перестановкой из чисел 1, 2, …, n называют расположение этих чисел в каком-то определённом порядке. Например, 3, 2, 1, 4 – перестановка из чисел 1, 2, 3, 4.

Пусть дана какая-то перестановка j₁,j₂,…,j_n из чисел 1, 2, …, n. Обозначим её сокращённо J и запишем

J = (j₁,j₂,…,j_n).

Назовём инверсией в перестановке J любую пару чисел в этой перестановке, из которых большее расположено левее меньшего.

Пример. В перестановке (3, 2, 1, 4) имеются 3 инверсии: (3, 2), (3, 1), (2, 1).

Будем обозначать общее число инверсий в перестановке J через 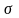(J). Перестановка J называется чётной, если число (J) – чётное, и нечётной , если число (J) –нечётное.

Определители n-ного порядка.

Рассмотрим квадратную таблицу, составленную из 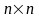чисел. Такую таблицу называют квадратной матрицей порядка n.Число, стоящее в i – той строке и j – том столбце таблицы обозначают a_ij.

.

Выберем какие-либо n элементов так, чтобы они находились в разных строках и в разных столбцах. Условимся любой такой набор из n элементов матрицы называть допустимым.

Рассмотрим какой-то допустимый набор из n элементов. Расположим элементы этого набора в определённом порядке: сначала элемент 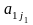, взятый из первой строки, затем элемент 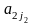из второй строки и т.д.. Итак, расположим элементы допустимого набора в виде последовательности

(3)

Числа j₁,j₂,…,j_n – номера столбцов, которых находятся выбранные элементы; по условию эти числа различны. Следовательно, строка j₁,j₂,…,j_n не что иное, как набор чисел 1, 2, …, n , записанном в определённом порядке. Обозначим эту строку сокращённо через J. Итак,

J = (j₁,j₂,…,j_n)-

некоторая перестановка из чисел 1, 2, …, n.

Если теперь для каждого допустимого набора (3) составить произведение 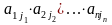всех элементов, входящих в этот набор, умножить его на +1 или –1 в зависимости от чётности или нечётности перестановки J, а затем все такие произведения сложить, то получим выражение

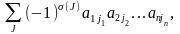
которое называется определителем матрицы n –ого порядка.

Определение. Определителем матрицы (1) называют выражение

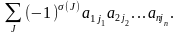= (4)