Матрицы.

Прямоугольная таблица чисел

,

состоящая из m строк и n столбцов называется матрицей размера

m × n . Числа а₁₁ ,а ₁₂, …, а_mn называются её элементами. Часто вместо подробной записи используют сокращённую: А = (а_ij ).

Если число строк матрицы равно числу её столбцов, то матрица называется квадратной.

Множество всех элементов квадратной матрицы, которые лежат на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним, - побочной диагональю.

Квадратная матрица называется диагональной, если все её элементы, не лежащие на главной диагонали, равны 0.

Две матрицы А = (а_ij ) и В = ( b_ij ) называются равными, если число их строк и столбцов равны и если равны элементы, стоящие на соответственных местах этих матриц: а_ij = b_ij при любых i и j.

Умножение матрицы на число и сложение матриц.

По определению, чтобы умножить матрицу А на число k, нужно каждый элемент матрицы А умножить на число k.

Например,

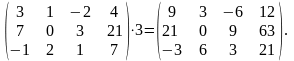
Складывать можно только матрицы с одинаковым числом строк и столбцов. Суммой матриц А = (а_ij) и В = (b_ij ) называется матрица С = (с_ij ), элементы которой равны суммам соответственных элементов матриц А и В: с_ij = а_ij + b_ij при любых i и j.

Например,

Матрица, все элементы которой равны 0, называется нулевой и обозначается через 0. Для любой матрицы А имеем А + 0 = А.

Матрица А· (-1) называется противоположной А и обозначается –А. Вместо А + ( -В ) пишут А – В.

Свойства умножения матрицы на число и сложения матриц (А, В, С- матрицы, k,l – числа).

1. А (k l) = (А k) l.

2. А + В = В + А.

3. ( А + В) + С = А + (В + С).

4. А (k + l) = А k + А l.

5. ( А + В) k = А k + Вk.

Умножение матриц.

Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица АВ, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В:

Запишем матрицы А и В в виде

А = 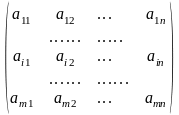, В =

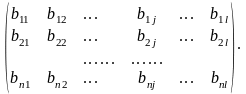
Обозначим элементы матрицы АВ через с_ij , 1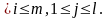 Тогда

АВ =

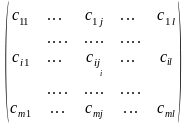
По определению, элемент с_ij матрицы АВ равен произведению i – той строки матрицы А на j –тый столбец матрицы В, т.е.

с_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj.

Пример. Найти произведение АВ, если

А =

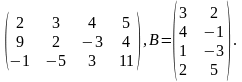
Матрица АВ является матрицей размера 3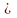 2. Вычисляем элементы с_ij

матрицы АВ. Имеем:

с₁₁ = 2· 3 + 3 ·4 + 4 ·1 + 5 ·2 = 32;

с₁₂ = 2· 2 + 3 ·(-1) + 4 ·(-3 ) + 5 ·5 = 14;

с₂₁ = 9 ·3 + 2 ·4 + (-3) ·1 + 4· 2 = 40;

с₂₂ = 9 ·2 + 2· (-1) + (-3)·(-3) + 4 ·5 = 45;

с₃₁ = (-1)· 3 + (-5) ·4 + 3 ·1 + 11· 2 = 2;

с₃₂ = (-1)· 2 + (-5) ·(-1) + 3· (-3) + 11 ·5 = 49.

Итак, АВ =

Свойства умножения матриц.

1. (АВ)k = (Ak)B = A (Bk), k – число.

2. ( А + В) С = АС +ВС.

3. С (А + В) = СА + СВ.

4. ( АВ)С = А ( ВС ) (ассоциативность).

5. АВ ВА (некоммутативность).

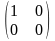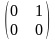Пример. А = , В = , АВ = , ВА = .

Матрицы А и В называются перестановочными, если АВ = ВА.