9. Мішаний добуток векторів та його властивості.

_{Нехай дано три вектори і Розглянемо добутки цих векторів, утворені за допомогою двох видів добутків скалярного та векторного}

_{Результат першого добутку скаляр . Результат другого вектор, який називається подвійним добутком або векторно- векторним добутком трьох даних векторів. Для знаходження подвійного векторного добутку використовують формули.}

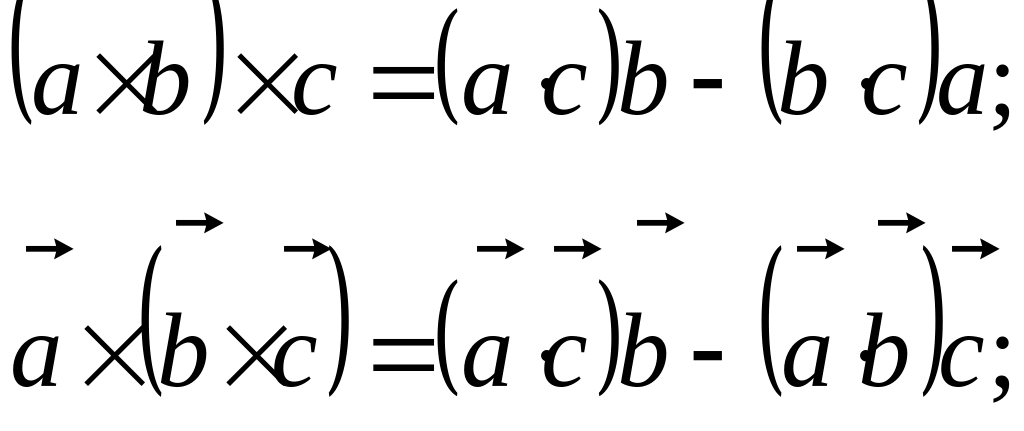
_{Результат третього добутку скаляр, який називається мішаним або векторно-скалярним добутком трьох векторів.}

_{Означення: Мішаним добутком векторів і називається скалярний добуток вектора на вектор .}

_{Властивості мішаного добутку}

1. _{При переставлені будь-яких двох множників мішаний добуток змінить знак на протилежний. Наприклад}

2. _{При циклічному переставлені множників мішаний добуток не змінюється.}

3. _{У мішаному добутку знаки векторного та скалярного добутків можна міняти}

_{місцями}

_{Зауваження: З урахуванням властивості 3 мішаний добуток позначають просто}

_.

4. _{Вектори і компланарні тоді і тільки тоді коли їх мішаний добуток дорівнює 0.}

_{і компланарні}

_{Доведення : Якщо вектори і компланарні, то вони лежать або в паралельних площинах, або в одній площині. Вектор , очевидно перпендикулярний до вектора , тому їх скалярний добуток дорівнює 0.}

_{Якщо і компланарні, то і лежить з векторами і в одній площині, тобто вектори і компланарні.}

5. Якщо вектори і утворюють праву трійку, то їх мішаний добуток додатній, а якщо ліву, то від’ємний.

6. Модуль мішаного добутку трьох векторів дорівнює обєму паралелепіпеда, побудованого на цих векторах віднесених до спільного початку.

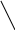
0

Доведення: Побудуємо на трьох векторах і паралелепіпед. Його об’єм , де S- площа основи, h- висота. Але ,

(+, якщо і утворюють праву трійку , -, якщо ліву)

.

Мішаний добуток в координатні формі

Нехай вектори і задані координатами в ПДСК.

, , .

Знайдемо їх мішаний добуток:

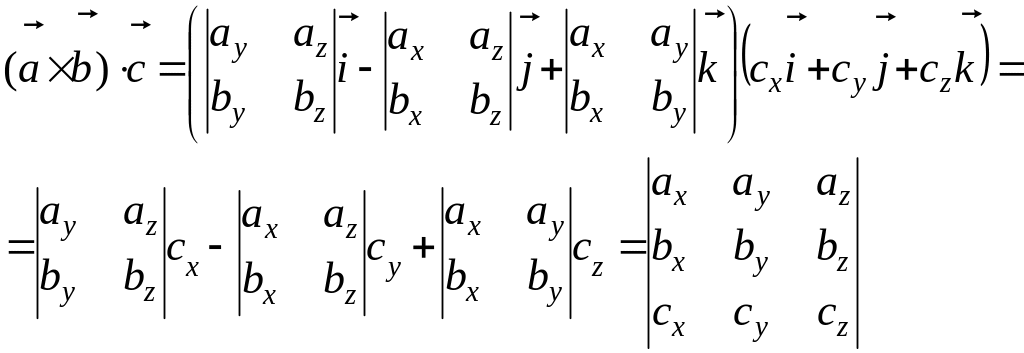
Отже векторний добуток трьох векторів, заданий координатами в ПДСК, визначається за формулою: ;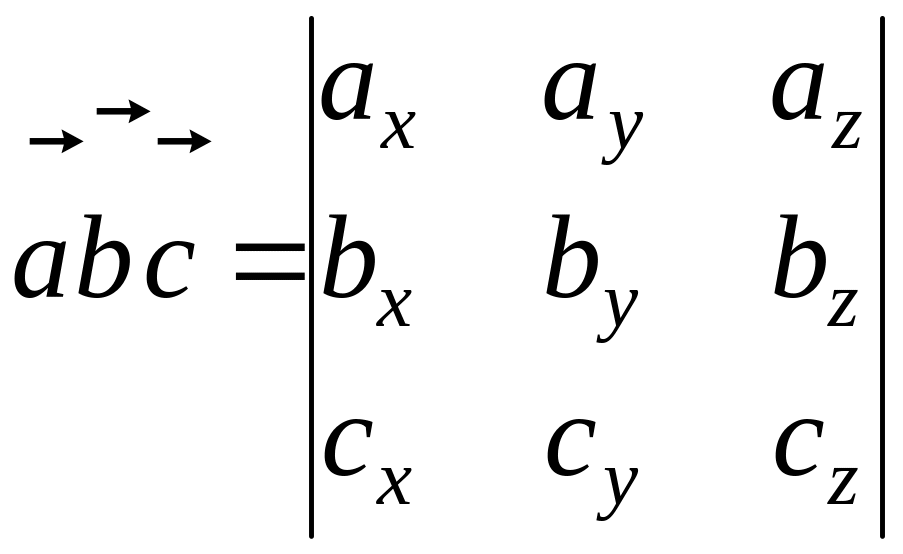

Приклад: Довести, що точки А(0; 1; 2), В(-2; 0; -1), С(-1; 5; 8), Д(1; 6; 11) лежать в одній площині.

Означення: 4 точки лежать в одній площині, якщо вектори , , компланарні. Знаходимо вектори: =(-2;-1;-3), =(-1;4;6), =(1;5;9).

За властивістю 4, якщо =0, то вектори компланарні. Перевіримо компланарність векторів , і .

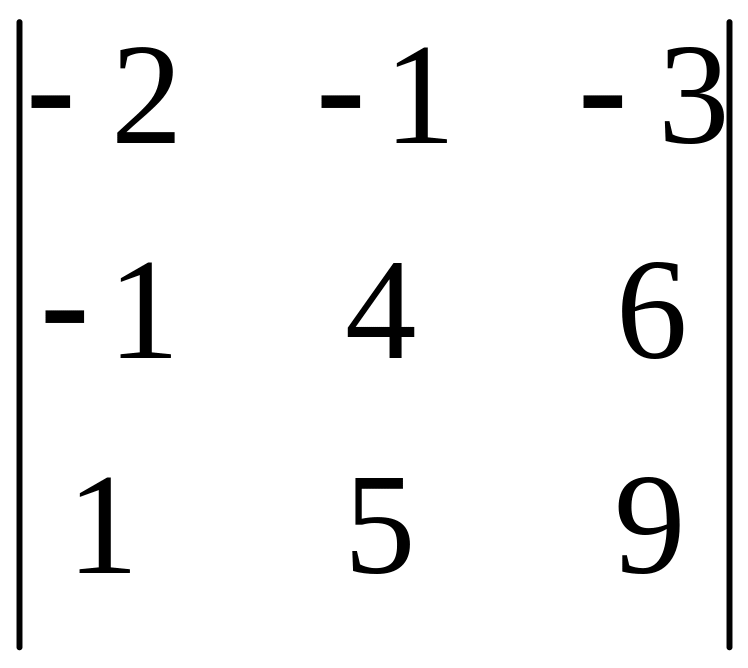= =-72+15-6+12+60-9=0.

Отже, вектори , і компланарні, тому задані точки лежать в одній площині.

22