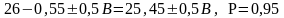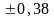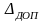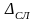Решение:

В результате n=9 измерений величины x₀ получен массив результатов измерений, который на языке математической статистики называется выборкой, элементы этого массива называются выборочными значениями измеряемой величины, а их количество - объемом выборки.

Вариационный ряд образуется путем перестановки исходного массива результатов многократных измерений в порядке их возрастания. Такая перестановка получается естественным путем при нанесении результатов на числовую ось. Элементы нового массива получают новые порядковые номера, и эти новые номера заключаются в круглые скобки:

.

Получаем вариационный ряд:

1	X(1) =25,57
2	X(2) =25,69
3	X(3) =25,74
4	X(4) =25,61
5	X(5) =25,73
6	X(6) =25,59
7	X(7) =25,78
8	X(8)= 25,66
9	X(9)= 25,79

Х_мах=25,79;

Х_мин=25,57.

По таблице 2 найти граничное значение β_гр по вероятности Р=0.95 и объему выборки n =9.

Таблица 3

Распределение случайных величин Груббса-Смирнова

№
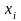
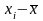
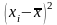
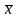
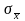
1	25,57	-0,11	0,0121	25,68	0,082	0,027
2	25,69	0,01	0,0001
3	25,74	0,06	0,0036
4	25,61	-0,07	0,0049
5	25,73	0,05	0,0025
6	25,59	-0,09	0,0081
7	25,78	0,1	0,01
8	25,66	-0,02	0,0004
9	25,79	0,11	0,0121
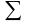(xi-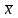 )2 = 0,0538

Наиболее распространенной точечной оценкой математического ожидания является среднее арифметическое значение результатов многократных измерений, то есть выборочных данных:

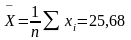
Рассчитаем среднеквадратическое значение рассеяния результатов многократных измерений по формуле 7:

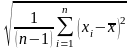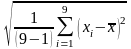= ; = = 0,082 (7)

Среднеквадратическое значение случайной погрешности результатов:

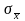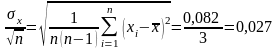= (8)

Обработка результатов многократных измерений.

Исключение из ряда измерений результатов с грубыми погрешностями.

Выделить из результатов измерения минимальное X_min=25,57, максимальное X_max = 25,79 значения и вычислить отношения V₁ и V₂

V₁=(X_max - )/ ; (9)

V₂=( - X_min)/ . (10)

V₁=(25,79 -25,68)/ 0,082=1.34; V₂=(25,68- 25,57)/ 0,082=1.34;

Значение β_гр=2,29. Обе величины V₁ и V₂ меньше, чем граничное значение, поэтому результатов с грубыми погрешностями нет.

Оценка доверительного интервала для истинного значения измеряемой

величины при доверительной вероятности P=0,95

Доверительный интервал - интервал, который накрывает действительное значение оцениваемой величины с заданной вероятностью P.

Из расчетов, проведенных выше, известно:

• среднее арифметическое значение оцениваемой величины =25,68,

• среднеквадратическое значение случайной погрешности результатов =0,027=0,028

При заданном значении доверительной вероятности Р =0,95 и числе измерений n по таблицам определяют коэффициент Стьюдента t_p

Для доверительной вероятности Р=0,95 и числе измерений n=9 коэффициент Стьюдента t_p= 2.23.

Если неизвестна (не задана) приборная погрешность, то границы доверительного интервала 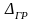определяют по формуле:

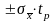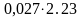= = = 0,06 (11)

Окончательный результат многократных измерений записывается в виде:

х = ; при Р=0,95.

х = 25,68 0,06В

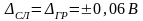
Определим результат измерений и его суммарную погрешность, представленные в таблице 3:

Таблица 4

Результаты измерений погрешностей

№п/п	Наименование погрешности	Обозначение	Величина, В
1	Погрешность прибора класса точности 0,025/0,05
2	Погрешность прибора температурная		0,15
3	Методическая погрешность		- 0,55
4	Случайная составляющая		0,06

Доверительные границы погрешности результата измерения можно вычислить по формуле

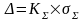, (12)

Где:

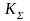• - коэффициент, зависящий от соотношения случайной и систематической погрешности;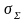

• - оценка суммарного среднеквадратического отклонения результата измерения

• определяется по формуле 13 и 14:

(13)

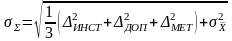(14)

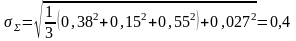
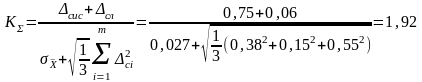
Результат:

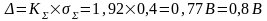
Итоговый результат при многократных измерениях: 25,68 0,8 В, Р=0,95

Вывод: При многократных измерениях случайная составляющая погрешности значительно уменьшается. Если в результат измерения внести поправку на явно выраженную методическую погрешность, то результат измерения будет выглядеть следующим образом:

;

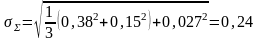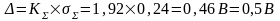
Результат: