
- •Тема 5 математико-статистичні методи фінансового аналізу
- •7. До екстенсивних факторів економічного розвитку належить:
- •8. Узагальнена модель факторної системи виражається у вигляді математичної формули:
- •9. Сутність прийомів елімінування полягає в:
- •10. У випадку відсутності чіткої черговості зміни факторів проведення фінансового аналізу мультиплікативних і кратних моделей здійснюється:
- •11. До середніх величин відносять:
- •12. Середня квадратична обчислюється:
- •13. Темпом зростання називається:
- •14. За допомогою кореляційного аналізу здійснюється:
- •20. До методів аналізу розвитку фінансово-економічних ситуацій належать:
- •21. Сутність аналізу чутливості полягає:
Тема 5 математико-статистичні методи фінансового аналізу
Програмна анотація
Кореляційний зв'язок та його особливості. Перевірка нормальності розподілу. Сутність багатофакторного регресійного аналізу. Метод побудови рівняння регресії. Перевірка значимості рівняння регресії. Етапи практичної реалізації кореляційно-регресійного аналізу. Методи сучасного факторного аналізу. Застосування коваріаційного аналізу.
Кореляційний аналіз є методом установлення і визначення тісноти зв'язків між спостереженнями, які можна вважати випадковими і вибраними із сукупності, розподіленої за багатомірним нормальним законом. Кореляційним називається такий статистичний зв'язок, коли різним значенням однієї змінної відповідають різні середні значення іншої змінної. Кореляційний аналіз установлює лише факт ступеня тісноти зв'язку, не викриваючи його причин.
У фінансовому аналізі найчастіше використовують лінійний коефіцієнт кореляції між двома ознаками х і у:
r
=
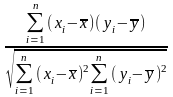 , (2.30)
, (2.30)
де
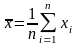 ,
,
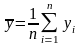 .
.
Значення коефіцієнта кореляції змінюються від -1 до +1. Значення r = -1 свідчить про наявність обернено пропорційного функціонального зв'язку між ознаками, що вивчаються; якщо значення r = +1, має місце функціональна прямо пропорційна залежність. Значення коефіцієнта r, наближене до 0, передбачає відсутність лінійного зв'язку між ознаками. Інші значення коефіцієнта кореляції свідчать про наявність стохастичного зв'язку, причому чим більше значення наближається до 1, тим тіснішим він є. На практиці існує таке умовне правило: якщо | r | < 0,3 зв'язок вважають слабким; при 0,3 < | r | < 0,7 — зв'язок середньої тісноти; | r | > 0,7 — тісний зв'язок.
Не існує загальноприйнятого критерію перевірки нормальності спільного розподілу змінних, що аналізуються. Як правило, обмежуються перевіркою нормальності окремих одномірних розподілів. За умови невеликих виборок така процедура може здійснюватися за допомогою показників асиметрії й ексцесу.
Коефіцієнт асиметрії розраховується за формулою
Аs
=
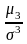 , (2.31)
, (2.31)
де
σAs
=
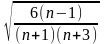 ;
;
μ3
=
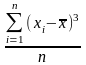 ;
;
п — кількість спостережень.
Розподіл вважається симетричним при As = 0. Чим більшим є значення As, тим більш асиметричним є розподіл змінної, що аналізується.
Крутизна розподілу даних, або ступінь опуклості його вершини, характеризується показником ексцесу:
Ex
=
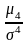 -
3
, (2.32)
-
3
, (2.32)
де
σEx
=
 ;
;
μ4
=
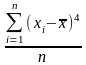 .
.
У випадку нормального розподілу Ех = 0. Значний додатний ексцес означає, що в сукупності даних є ядро, яке слабко змінюється за даною ознакою, оточене поодинокими значеннями, що сильно від нього відрізняються. Від'ємне значення ексцесу свідчить про відсутність такого ядра.
У разі якщо розподіл сильно відрізняється від нормального, найчастіше застосовують відсіювання аномальних значень спостережень або включення до сукупності додаткових спостережень.
Регресійний аналіз — метод установлення аналітичного відображення стохастичної залежності між ознаками, що досліджуються. Рівняння регресії показує, як у середньому змінюється результативний (залежний) показник у при зміні будь-якого з незалежних показників лсг:
у = ∫ х1, х2,...,хп) . (2.33)
Регресійний аналіз використовується для прогнозування і планування.
На відміну від кореляційного аналізу, регресійний аналіз дає формалізоване вираження зв'язку між аналізованими ознаками. Якщо кореляційний аналіз визначає взаємозв'язок факторів, то регресійний аналіз — причинно-наслідкову односторонню залежність, що показує, яким чином зміна факторних ознак впливає на результативну ознаку.
У багатофакторному регресійному аналізі використовують лінійні моделі на зразок:
Y = a0+a1x1+a2x2+... + anxn . (2.34)
Побудова рівняння регресії, як правило, здійснюється за допомогою методу найменших квадратів, сутність якого полягає в мінімізації суми квадратів відхилень фактичних значень результативної ознаки від її розрахункових значень:
S
=

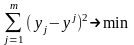 , (2.35)
, (2.35)
де т — кількість спостережень;
y = а0+ а1х + а2х +... + апх — розрахункове значення результативного показника.
Після побудови рівняння регресії необхідно перевірити його значимість: установити, чи не є отримана залежність, виражена рівнянням регресії, випадковою, тобто чи можливо використовувати її в прогнозних цілях і для факторного аналізу. Перевірка може бути виконана розрахунком середнього відносного лінійного відхилення — середньої похибки апроксимації:
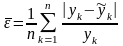 100%
, (2.36)
100%
, (2.36)
де ук — k-те значення результативного показника;
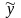 к
—
вирівняне (розраховане по рівнянню
регресії) k-те
значення
результативного показника.
к
—
вирівняне (розраховане по рівнянню
регресії) k-те
значення
результативного показника.
Модель вважається придатною для практичного використання, якщо похибка апроксимації не перевищує 15 %.
В економічних дослідженнях кореляційний і регресійний аналіз часто поєднуються в один — кореляційно-регресійний. У результаті такого аналізу будується регресійна залежність і розраховуються коефіцієнти її тісноти і значимості.
Практична реалізація кореляційно-регресійного аналізу включає низку етапів:
якісний аналіз (постановка завдання, вибір результативної і факторних ознак);
збір інформації і її первинна обробка (групування виключення аномальних спостережень, перевірка нормальності одномірних розподілів);
визначення виду моделі (будуються аналітичні групування і графіки);
перевірка однорідності сукупності (по кожній з ознак розраховується коефіцієнт варіації; якщо його значення не перевищує 33 %, сукупність визнається однорідною за даною ознакою; якщо дана умова не виконується, проводиться повторна процедура відсіювання спостережень з аномальними значеннями ознаки);
перевірка нормальності розподілів ознак (розрахунок показників асиметрії й ексцесу);
відбір факторів до моделі, маючи на увазі, що кількість спостережень повинна як мінімум у 6—8 разів перевищувати кількість факторів у моделі;
ліквідація мультиколінеарності (взаємозалежності) факторів і уточнення набору показників (розраховуються парні коефіцієнти кореляції по всіх ознаках, що аналізуються; два фактори не можуть одночасно включатися до моделі, якщо вони пов'язані між собою тісніше, ніж кожен з них з результативним показником);
побудова рівняння регресії за допомогою системи нормальних рівнянь;
перевірка значимості побудованого рівняння (розрахунок коефіцієнта множинної кореляції);
10) оцінка результатів аналізу і підготовка рекомендацій щодо їх практичного використання.
До методів сучасного факторного аналізу входять методи багатофакторних залежностей за умови, що фактори суттєво корелюють між собою. Сучасний факторний аналіз дає можливість спільної обробки великої кількості взаємозв'язаних (корелюючих) факторів. Апарат сучасного факторного аналізу дозволяє звести десятки вихідних ознак (факторів) до кількох узагальнених, які не спостерігаються безпосередньо при дослідженні, але з'являються в моделі як лінійні комбінації вихідних ознак і підлягають певній інтерпретації. Узагальнені фактори не корелюють між собою, а тому їх можна використовувати для побудови регресійних рівнянь.
Методи сучасного факторного аналізу спрямовані на вирішення таких завдань:
пошук прихованих, але об'єктивно існуючих закономірностей між факторами і оцінка їх впливу на результативні показники;
опис явища, що вивчається, значно меншою кількістю узагальнених факторів;
виявлення стохастичного зв'язку між вихідними й узагальненими факторами;
побудова рівняння регресії на базі узагальнених факторів.
Найбільшого поширення серед методів даної групи набули метод головних компонент і власне сучасний факторний аналіз.
Метод головних компонент передбачає рівну кількість узагальнених факторів (головних компонент) і вихідних факторних ознак. Однак головні компоненти впорядковано згідно з внеском кожної компоненти у вихідну дисперсію факторів (наприклад, перша компонента враховує 40 % загальної дисперсії, друга — 25 третя — 15 четверта— 10 % тощо; для побудови рівняння регресії аналітик може обмежитися першими трьома узагальненими факторами, які в сумі становлять 80 % дисперсії, тобто значною мірою пояснюють варіацію результативної ознаки).
Сучасний факторний аналіз дає змогу звести вихідні факторні ознаки до меншої кількості узагальнених факторів, кожен з яких є лінійною комбінацією вихідних ознак.
Недоліком описаних методів є складність математичного апарату, складність інтерпретації узагальнених факторів. Тому дані методи застосовуються переважно в тематичному фінансовому аналізі.
Дисперсійний аналіз— це статистичний метод, який дозволяє підтвердити або заперечити гіпотезу про те, що дві вибірки даних належать до однієї генеральної сукупності.
Дисперсійний аналіз часто застосовується спільно з методами групування. Завдання його проведення полягає в оцінці істотності різниці між групами. Для цього визначають групові дисперсії, а потім за статистичними критеріями перевіряють значення відмінності між групами.
Кластерний аналіз — один з методів багатовимірного аналізу, призначений для групування (кластерізації) сукупності, елементи якої характеризуються багатьма ознаками. Кожне спостереження, що характеризується значеннями кількох показників, можна уявити як точку в просторі цих показників, значення яких розглядаються як координати в багатовимірному просторі.
Головним критерієм кластеризації є те, що відмінності між кластерами повинні бути більш істотними, ніж між спостереженнями, віднесеними до одного кластера.
У процесі фінансового аналізу постійно доводиться мати справу з інформаційними масивами у вигляду сукупностей показників. У загальному вигляді вони поділяються на три групи: часову, просторову і просторово-часову.
Часові сукупності подані рядами динаміки (динаміка дохідності акцій підприємства).
Просторові сукупності — це сукупність показників по групі об'єктів на певну дату чи за певний період (дані про товарообіг за певний період по ряду підприємств).
Просторово-часові сукупності — сукупності показників по групі об'єктів за ряд періодів (дані про дохідність облігацій кількох емітентів у динаміці). Просторово-часові сукупності узагальнюють часові і просторові.
Методика обробки перших двох видів сукупності зводиться до кореляційно-регресійного аналізу. Техніка аналітичної обробки просторово-часових сукупностей є складною як у технічному, так і в процедурному планах. З іншого боку, просторово-часова сукупність є більш інформативною, а показники, що характеризують виявлені в результаті її обробки закономірності, є більш стійкими і частіше застосовуються на практиці.
Для кількісної обробки просторово-часових сукупностей використовують ряд методів.
Метод попереднього усереднення даних передбачає усереднення вихідних зданих за кожним показником і за кожним об'єктом. Таким чином просторово-часова сукупність зводиться до просторової, до якої можна застосувати кореляційно-регресійний аналіз.
Метод об'єкто-періодів використовується в разі, коли сукупність, що досліджується, невелика за обсягом. У такому разі весь масив даних розглядається як одна сукупність, одиницями спостереження якої є так звані об'єкто-періоди. Далі проводиться кореляційно-регресійний аналіз.
Метод усереднення параметрів однорічних рівнянь передбачає побудову рівнянь регресії для кожного, року після чого простим усередненням параметрів цих рівнянь (коефіцієнтів регресії) знаходять усереднене рівняння, яке й використовується як характеристика просторово-часової сукупності.
Коваріаціпний аналіз, що поєднує властивості дисперсійного аналізу, призначеного для вивчення впливу на результативну ознаку якісних ознак, і регресійного аналізу, призначеного для вивчення зв'язків кількісних ознак, забезпечує побудову за спеціальними алгоритмами так званої середньої форми рівняння регресії.
Саме коваріаційний аналіз дає найкраще усереднення в просторово-часовому аспекті, тобто рівняння регресії, одержане за даним методом, дає найбільш достовірну характеристику закономірного зв'язку, притаманного сукупності показників, що вивчаються.
Team 6
МЕТОДИ ТЕОРІЇ ПРИЙНЯТТЯ РІШЕНЬ
Програмна анотація
Методи аналізу розвитку ситуацій та фактори, що визначають важливість їх застосування. Імітаційне моделювання та фактори, що визначають об'єктивність його результату. Класифікація ситуацій, в яких відбувається прийняття фінансово-економічних рішень. Метод лінійного планування та сфера його застосування. Сутність методу аналізу чутливості
З розвитком обчислювальної техніки дедалі більшого поширення набувають методи аналізу розвитку ситуацій, що базуються на варіюванні поєднанням і значеннями різних факторів, що їх визначають.
Важливість застосування методів аналізу розвитку ситуацій визначається кількома обставинами:
діяльність будь-якого суб'єкта господарювання залежить від багатьох факторів;
переважна більшість таких факторів є взаємозв'язаними;
деякі фактори можна регулювати;
змінюючи набір ключових параметрів і (або) їх значення, можна змоделювати ситуацію і завдяки цьому уявити тенденції основних результативних показників, вирахувати орієнтири їх можливих значень;
вибравши найбільш прийнятний варіант розвитку подій і задаючи відповідні значення виділених факторів, можна певною мірою регулювати поведінку системи, впливати на значення її основних показників.
Сутність імітаційного моделювання полягає у створенні у спеціалізованому програмно-апаратному середовищі конкретної фінансово-господарської ситуації через вибір: моделі або набору моделей, що описують ситуацію; масиву параметрів у рамках виділених моделей; сукупності результативних показників, що залежать від виділених параметрів; набору значень параметрів.
Зробивши ряд розрахунків, можна вибрати набір параметрів і їх значень, якими і надалі потрібно управляти (наприклад, не допускати збільшення дебіторської заборгованості вище від певної межі).
Імітаційне моделювання — досить суб'єктивний варіант обґрунтування дій з управління розвитком подій. Об'єктивність результату великою мірою визначається проблемністю системи моделей, оскільки набір параметрів і їх значення дуже мінливі.
Найбільшого практичного поширення набули моделі, що описують функціональні або жорстко детерміновані зв'язки, коли кожному значенню факторної ознаки відповідає невипадкове значення результативного показника.
Як приклад можна навести модель факторного аналізу фірми «Дюпон». Підставляючи в дану модель прогнозні значення різних факторів (виручки від реалізації, ступеня фінансової залежності тощо) можна розрахувати прогнозне значення одного з основних показників ефективності — коефіцієнта рентабельності власного капіталу.
Ще один варіант застосування ситуаційного аналізу для прогнозування ґрунтується на оцінці ризику.
Прийняття фінансово-економічних рішень може здійснюватися в одній з таких ситуацій: в умовах визначеності, ризику, невизначеності і конфлікту. Перша ситуація має місце в разі, коли можливо з прийнятною точністю передбачити наслідки прийнятого рішення. В умовах ризику діапазон можливих наслідків прийнятого рішення більш широкий, однак значення наслідків і ймовірність їх вияву піддаються кількісній оцінці. В умовах невизначеності таку оцінку зробити неможливо, тобто неможливо перерахувати всі можливі наслідки та визначити ймовірність їх виникнення. В умовах конфлікту прийняте рішення ускладнюється не лише можливістю вияву дії випадкових факторів, а й необхідністю врахування безумовної свідомої й активної протидії учасників конфліктної ситуації, причому кількість цих учасників, їх інформаційні та інші ресурси можуть бути заздалегідь невідомі.
В умовах ризику для вибору варіанта дії застосовується ймовірносний підхід, що передбачає прогнозування можливих наслідків і присвоєння їм імовірностей. При цьому користуються відомими типовими ситуаціями, попереднім розподілами ймовірностей, суб'єктивними оцінками, зробленими аналітиком самостійно або з залученням групи експертів.
При цьому послідовність дій аналітика така:
прогнозуються можливі наслідки Rk, k=1, 2, ..., п; як Rk можуть виступати різні показники: дохід, прибуток, вартість надходжень, що очікуються тощо;
кожному наслідку присвоюється відповідна ймовірність Pk, причому
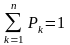 ; (2.37)
; (2.37)
— вибирається критерій (наприклад, максимізація математичного очікування прибутку):
E(R)
=
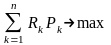 ;
(2.38)
;
(2.38)
— вибирається варіант, що відповідає вибраному критерію.
Метод лінійного програмування найбільш поширений у прикладних економічних дослідженнях. За його допомогою в аналізі фінансово-господарської діяльності вирішується ряд завдань, що стосуються процесу планування діяльності. Метод дозволяє зна-ходити оптимальні параметри випуску і способи якнайкращого використання наявних ресурсів.
Термін «програмування», що був уведений у вітчизняну економічну літературу в 60-х роках XX ст., має кілька значень. По-перше, цим терміном позначається процес підготовки спеціальної програми для ЕОМ; по друге, програмування використовується як синонім термінів «планування» і «прогнозування».
Сутність методу лінійного програмування полягає в пошуку максимуму або мінімуму вибраної згідно з інтересами аналітика цільової функції за певних обмежень.
Для успішного планування фінансово-господарської діяльності підприємства бажано передбачити зміни, які можуть відбутись у майбутніх цінах на сировину і кінцеву продукцію підприємства, можливе падіння або зростання попиту. Для вирішення даного завдання в умовах невизначеності, коли неможливо точно передбачити, якими будуть фактичні значення тієї чи іншої величини через деякий час, виконується аналітична процедура, яка називається аналізом чутливості.
Аналіз чутливості полягає у визначенні, що буде, коли один або кілька факторів змінять свою величину. Теоретично кількість поєднань значень факторів є величиною, наближеною до нескінченності, а тому аналіз їх зміни неможливо виконати без застосування комп'ютерної техніки.
Розглянемо сутність даного методу на прикладі моделі звіту про прибуток і витрати підприємства, наведеного в табл. 2.4.
Таблиця 2.4
ЗВІТ ПРО ПРИБУТКИ І ВИТРАТИ ПІДПРИЄМСТВА
Показник |
Індекс |
Значення |
Кількість проданих одиниць продукції |
Q |
1000 |
Ціна за одиницю, грн |
р |
5000 |
Виручка, грн |
R |
5 000 000 |
Змінні затрати, грн |
VC |
3 000 000 |
Валовий дохід, грн |
— |
2 000 000 |
Постійні витрати, грн |
FC |
1 000 000 |
Оподаткований прибуток, грн |
P0 |
1 000 000 |
Сума податку на прибуток, грн, нарахована за ставкою Т =40% |
N |
400 000 |
Чистий прибуток, грн |
π |
600 000 |
Припустимо, що чистий прибуток підприємства визначається виручкою за винятком всіх витрат (змінних і постійних) і податку на прибуток. У такому разі факторна модель прибутку матиме такий вигляд:
π = R – TC – N , (2.39)
де ТС — повні витрати.
З таблиці видно, що ринкова ціна за одиницю продукції складає 5000 грн, а змінні витрати на одиницю продукції (z) становлять 3000 грн. Звідси випливає:
повні витрати: ТС = FC + VC = FC + z × Q; (2.40)
оподаткований прибуток: P0 = R-FC - z × Q; (2.41)
чистий прибуток: р = [(р - z) × Q - FC] × (1 - T). (2.42)
Розглянемо методику оцінки чутливості чистого прибутку на прикладі зміни лише одного фактора— обсягу продажу за незмінності всіх інших. Значення похідної по Q має вигляд:
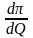 = (p
- z)
×
(l
- T)
. (2.43)
= (p
- z)
×
(l
- T)
. (2.43)
За допомогою вищенаведеної формули можна визначити, на скільки зміниться прибуток за зміни кількості реалізованих екземплярів на одиницю:
(5000 - 3000) х (1 - 0,4) = 1200 грн.
Аналіз чутливості дозволяє визначити силу реакції результативного показника на зміну незалежних (мінливих) факторів. На практиці поширений варіант аналізу чутливості, коли побудовану модель розглядають для трьох ситуацій: найліпша, найбільш імовірна, найгірша.
Тема 7
МЕТОДИ ФІНАНСОВИХ ОБЧИСЛЕНЬ
Програмна анотація
Логіка методів оцінки ефективності фінансових операцій. Найпростіший вид фінансової операції. Відсоткова та облікова ставки. Процеси нарощування і дисконтування. Математичне і банківське дисконтування. Коефіцієнт дисконтування. Основні схеми відсоткового нарахування. Показник ефективної річної відсоткової ставки та методика його розрахунку. Оцінка грошових потоків як один з головних методів фінансового аналізу. Сутність грошових потоків пренумерандо і постнумерандо. Ануїтет і підходи до його визначення. Техніка оцінки безстрокового ануїтету.
Більшість рішень, які приймаються управлінським персоналом, є одномоментними в плані вияву спричинених наслідків рішеннями фінансового характеру, логіка яких виражається співвідношенням: доходи, які очікуються в результаті прийняття даного рішення, повинні певним чином переважати витрати, пов'язані з його підготовкою і реалізацією. Формалізованою основою подібних рішень є фінансові обчислення, що базуються на понятті часової вартості грошей. Найбільш часто фінансові обчислення застосовуються для оцінки інвестиційних проектів, в операціях на ринку цінних паперів, для оцінки бізнесу тощо.
Логіка методів оцінки ефективності фінансових операцій визначається такими положеннями:
практично кожну фінансово-господарську операцію можна виразити у фінансових термінах;
у переважній більшості випадків власне операції і їх наслідки «розтягнуті» в часі;
з кожною операцією можна ув'язати деякий грошовий потік;
грошові засоби повинні ефективно обертатися, тобто з часом приносити певний прибуток;
елементи грошового потоку, що належать різним часовим моментам, незіставні без певних перетворень;
перетворення елементів грошового потоку здійснюється шляхом застосування операцій нарощування і дисконтування;
нарощування і дисконтування можуть виконуватися за різними схемами і з різними параметрами.
Найпростішим видом фінансової операції є одноразове надання в борг деякої суми PV за умови, що через деякий час t буде повернута більша сума FV. Результативність подібної операції може бути охарактеризована через розрахунок отриманого приросту Д = FV - PV або через розрахунок деякого відносного показника. Абсолютні показники в переважній більшості випадків не підходять для подібної оцінки внаслідок їх незіставності в просторово-часовому аспекті. Тому користуються спеціальним коефіцієнтом, який розраховується відношенням приросту вихідної суми до базової величини і називається ставкою. Якщо як базова величина вибирається PV, одержуємо відсоткову ставку, а якщо FV— облікову ставку.
Отже, в будь-якій фінансовій операції завжди наявні три величини: PV, FV і ставка г, дві з яких задані, а одна є невідомою. Процес, в якому задані вихідна сума і відсоткова ставка у фінансових обчисленнях називається процесом нарощування. Процес, в якому задані очікувана в майбутньому до отримання сума і ставка (коефіцієнт дисконтування), називається процесом дисконтування. У першому випадку мова йде про рух грошового потоку від сучасного до майбутнього, а у другому— від майбутнього до сучасного. Якщо як коефіцієнт дисконтування використовується відсоткова ставка, ми маємо справу з математичним дисконтуванням, а в разі використання облікової ставки — банківським дисконтуванням.
Економічна сутність фінансової операції нарощування полягає у визначенні величини суми, яку буде або бажає мати інвестор після завершення операції. Оскільки FV = PV + PVxr і PV × r > 0, очевидно, що час генерує гроші, а отже вони, мають часову цінність.
Економічна сутність дисконтування полягає в часовому впорядкуванні грошових потоків різних часових періодів. Коефіцієнт дисконтування показує, який щорічний відсоток хоче (або може) мати інвестор від інвестованого капіталу. У даному разі величина PV показує поточну вартість майбутньої величини FV.
Надаючи грошові засоби в борг, власник отримує певних прибуток у вигляді відсотків, що нараховуються за певним алгоритмом протягом певного проміжку часу. Як правило, стандартним часовим інтервалом у фінансових операціях є рік. Тому найбільш поширеним є варіант, коли відсоткова ставка встановлюється у вигляді річної ставки, що передбачає одноразове нарахування відсотків після завершення року з моменту отримання коштів. Відомі дві основні схеми дисконтного нарахування: схеми простих і складних відсотків.
Схема простих відсотків передбачає незмінність бази, з якої відбувається нарахування.
Rn = P + P × r + ... + P × r = P ×(1 + n × r) , (2.44)
де Rn — розмір інвестованого капіталу через п років;
Р — вихідний інвестований капітал;
r — дохідність, виражена в частках одиниці.
Схема простих відсотків застосовується в практиці банківських розрахунків при нарахуванні відсотків по короткострокових кредитах з терміном погашення до одного року. Як показник п у такому випадку використовується величина, що характеризує питому вагу тривалості підперіоду.
Схема складних відсотків передбачає нарахування чергового річного доходу не з базової величини інвестованого капіталу, а з загальної суми, що включає також і раніше нараховані, але не використані інвестором відсотки. У цьому випадку відбувається капіталізація відсотків у міру їх нарахування, тобто база, з якої нараховуються відсотки, постійно зростає:
Fn = P × (1+ r)n. (2.45)
Показник (1 + r)n називається мультиплікуючим множником для одиничного платежу. Для зручності користувачів його показники розраховані для різних можливих значень r i n і наведені у вигляді спеціальних фінансових таблиць. Тоді формула алгоритму нарощування за схемою складних відсотків матиме вигляд:
Fn=P × FM1(r , n) , (2.46)
де FM1 (r, п) — мультиплікуючий множник.
У практиці фінансових і комерційних розрахунків нерідко визначається величина річного відсотка і частота його нарахування, відмінна від річної. В такому випадку розрахунок ведеться за формулою складних відсотків за підінтервалами і за ставкою, що дорівнює пропорційній частці вихідної річної ставки:
Fn = P × (1 + r / m)k×m , (2.47)
де r — оголошена річна ставка;
т — кількість нарахувань за рік;
k— кількість років.
Досить поширеними є фінансові контракти, що укладаються на період, відмінний від цілої кількості років, причому відсотки можуть нараховуватися не один раз за рік, а за певний базовий підперіод, визначений договором. У такому випадку користуються як методом нарахування складних відсотків, так і змішаним методом, коли використовується схема складних відсотків для цілої кількості базових періодів і схема простих відсотків для частини базового періоду:
Fn = P × (1 + r / m)w+f ; (2.48)
Fn = P × (1 + r / m)w × (1 + f + r / m) , (2.49)
де w — ціле число базових підперіодів у фінансовій операції;
f — дробова частина базового підперіоду;
r — річна ставка;
т — кількість нарахувань за рік.
У фінансових контрактах можуть передбачатися різні схеми нарахування відсотків. При цьому, як правило, обумовлюється мінімальна відсоткова ставка, переважно річна, яка не відображає реальної ефективності операції і не може бути використана для зіставлень. Для забезпечення порівняльного аналізу ефективності подібних контрактів використовують показник ефективної річної відсоткової ставки, який залежить від кількості внутрішньо-річних нарахувань:
re = (1 + r / т)т – 1 . (2.50)
Оцінюючи доцільність фінансових вкладень у той чи інший вид бізнесу, виходять з того, чи є рівень їх прибутковості (при допустимому рівні ризику) більшим, ніж рівень прибутковості вкладень у державні цінні папери. Використовуючи нескладні методи, роблять спроби проаналізувати майбутні доходи при мінімальному «безпечному» рівні прибутковості.
Головна ідея цих методів полягає в оцінці майбутніх надходжень Fn (у вигляді прибутку, відсотків, дивідендів) з позиції поточного моменту. Зробивши фінансові вкладення, інвестор, як правило, керується трьома постулатами: 1) проходить постійне знецінення грошей (інфляція); 2) темп зміни цін на сировину, матеріали й основні засоби, що використовуються підприємством, може істотно відрізнятися від темпів інфляції; 3) бажане періодичне нарахування (або надходження) прибутку в розмірі, не нижчому за певний мінімум. Базуючись на цих постулатах, інвестор повинен оцінити свої доходи в майбутньому і максимальну суму, яку можна вкласти в дане підприємство виходячи з його прогнозної рентабельності:
P
=
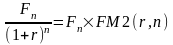 ,
(2.51)
,
(2.51)
де Fn — прибуток, що планується одержати в «-му році;
Р — поточна вартість, тобто оцінка величини з позиції поточного моменту;
r — коефіцієнт дисконтування.
Економічна сутність такого розрахунку полягає в такому: прогнозована величина грошових надходжень через п років (Fn) буде меншою з позицій поточного моменту і дорівнюватиме Р (оскільки знаменник дробу більший за одиницю). Також це значить, що для інвестора сума Р в даний момент і сума Fn через п років однакові за своєю цінністю.
Використовуючи дану формулу, можна зіставляти оцінку доходів від інвестицій, очікуваних протягом ряду років.
Множник FM2(r, k) = 1/(1 + r)k називається дисконтуючим множником для одиничного платежу. Його значення також розраховані і наведені у спеціальних таблицях. Економічна сутність дисконтуючого множника полягає у відображенні «сьогоднішньої» ціни однієї грошової одиниці майбутнього, тобто чому з позиції поточного моменту дорівнює грошова одиниця (наприклад гривня), що циркулює у сфері бізнесу через k періодів після моменту розрахунку при заданих відсотковій ставці r і частоті нарахування відсотка. Термін «сьогоднішня вартість» не слід сприймати буквально, адже дисконтування може бути виконане на будь-який момент часу, який не обов'язково збігається з поточним моментом.
Одним з головних елементів фінансового аналізу є оцінка грошового потоку, що генерується протягом ряду часових періодів у результаті реалізації певного проекту або функціонування того чи іншого виду активів. Елементи грошового потоку Сi можуть бути або незалежні, або пов'язані між собою певним алгоритмом.
Якщо надходження, що генеруються в рамках одного часового періоду, не розподілені в його рамках і мають місце на його початку, потік називається потоком пренумерандо. У протилежному випадку грошовий потік називається потоком постнумерандо.
На практиці більш поширеним є потік постнумерандо. Саме він лежить в основі методик аналізу інвестиційних проектів.
Оцінка грошового потоку може виконуватися в рамках розв'язання двох задач: прямої й оберненої. В першому випадку проводиться оцінка з позиції майбутнього (реалізується схема нарощування), а в другому — з позиції сучасності (реалізується схема дисконтування).
Пряма задача передбачає сумарну оцінку нарощеного грошового потоку, тобто в її основі лежить майбутня вартість. Якщо грошовий потік є регулярним нарахуванням відсотків на вкладений капітал за схемою складних відсотків, а в основі сумарної оцінки нарощеного грошового потоку лежить формула (2.45), майбутня вартість вихідного грошового потоку постнумерандо FVpst може бути оцінена як сума нарощених надходжень:
FVpst
=
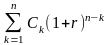 .
(2.52)
.
(2.52)
Обернена задача передбачає сумарну оцінку дисконтованого грошового потоку. У зв'язку з тим, що окремі елементи грошового потоку генеруються в різні часові інтервали, а гроші мають часову вартість, безпосереднє їх підсумовування неможливе. Після приведення грошового потоку до одного моменту часу за допомогою формули (2.51), розраховується загальна величина приведеного грошового потоку. Зокрема, приведена вартість грошового потоку постнумерандо PVpst d розраховується за формулою
PVpst
=
 . (2.53)
. (2.53)
Для потоків пренумерандо формули (2.52) і (2.53) матимуть такий вигляд:
FVpre = FVpst ×(1 + r); (2.54)
PVpre = PVpst ×(1 + r) . (2.55)
Слід зазначити, що об'єктивні результати розрахунків забезпечуються лише в тому випадку, коли інвестор не накопичує отримані грошові кошти, а постійно інвестує їх з метою отримання додаткового прибутку. Саме цим пояснюється використання в обох випадках капіталізації за схемою складних відсотків.
Одним з ключових понять у фінансових і комерційних розрахунках є поняття ануїтету.
Під ануїтетом розуміють окремий вид грошового потоку. Існує два підходи до його визначення. Згідно з першим ануїтет — це однонапрямлений грошовий потік, елементи якого мають місце через рівні інтервали. Другий підхід накладає додаткове обмеження, а саме: елементи грошового потоку однакові за величиною. Саме останній підхід дає можливість суттєвого спрощення алгоритму його оцінки.
Якщо кількість рівних часових інтервалів обмежена, ануїтет називається терміновим. В такому випадку С1= C2 = ... = Сn = А.
Для розв'язання прямої задачі оцінки термінових ануїтетів постнумерандо і пренумерандо при заданих величинах регулярного надходження А і відсоткової ставки г можна скористатися відповідними формулами
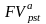 =
A
× FM3(r,
n)
; (2.56)
=
A
× FM3(r,
n)
; (2.56)
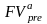 =
×
(1
+ r)
= A
× FM3
(r,
n)
×
(1
+ r)
, (2.57)
=
×
(1
+ r)
= A
× FM3
(r,
n)
×
(1
+ r)
, (2.57)
де
FM3
(r,
n)
=
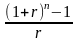 (2.58)
(2.58)
Множник FM3(r,гі) називається мультиплікуючим множником для ануїтету. Він показує, чому буде дорівнювати сумарна величина термінового ануїтету в одну грошову одиницю (наприклад гривню) на кінець дії його терміну. Множник FM3(r,ri) часто використовується у фінансових розрахунках, а оскільки його величина залежить лише від г і «, його можливі значення розраховані і зведені до спеціальних таблиць.
Для розв'язання оберненої задачі оцінки термінових ануїтетів постнумерандо і пренумерандо, що є основною при аналізі інвестиційних проектів, грошові потоки яких мають вигляд ануїтетних надходжень, можна скористатися такими формулами:
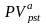 =
A
×
FM4(r%,
n)
; (2.59)
=
A
×
FM4(r%,
n)
; (2.59)
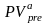 =
×
(1+
r)
= A
×
FM4(r,
n)
×
(1
+ r)
, (2.60)
=
×
(1+
r)
= A
×
FM4(r,
n)
×
(1
+ r)
, (2.60)
де
FM4(r,
n)
=
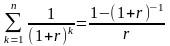 . (2.61)
. (2.61)
Множник FM4(r, n) називають дисконтуючим множником для ануїтету. Він показує, чому дорівнює з позиції поточного моменту величина ануїтету з регулярними грошовими надходженнями у розмірі однієї грошової одиниці, що продовжується п рівних періодів з заданою відсотковою ставкою г. Як і значення поперднього множника, можливі значення дисконтуючого множника для ануїтету розраховані і зведені до спеціальних таблиць.
При виконанні деяких фінансових розрахунків застосовується техніка оцінки безстрокового ануїтету. Ануїтет називають безстроковим у випадку, коли грошові надходження продовжуються досить тривалий час (як правило, 50 і більше років).
У такому випадку розв'язання прямої задачі не має сенсу. Обернена задача для ануїтету постнумерандо розв'язується за формулою
PV
=
 . (2.62)
. (2.62)
ПИТАННЯ ДЛЯ САМОСТІЙНОГО КОНТРОЛЮ
Які головні рівні виділяють при класифікації методів фінансового аналізу?
Чим відрізняються неформалізовані і формалізовані методи фінансового аналізу?
Для якої групи методів фінансового аналізу більшою мірою притаманний суб'єктивізм?
Назвіть основні групи формалізованих методів фінансового аналізу.
У чому сутність моделювання?
Назвіть основні типи моделей, що використовуються у фінансовому аналізі.
Які головні відмінності між дескриптивними, предикативними і нормативними моделями?
Наведіть приклади дескриптивних моделей. На чому вони базуються?
У чому відмінність між вертикальним і горизонтальним аналізом бухгалтерської звітності?
До якого типу моделей належить модель товарного балансу? Обгрунтуйте відповідь.
Наведіть приклади мультиплікативних і кратних фінансових моделей.
В яких випадках застосовуються стохастичні моделі факторного аналізу?
Назвіть методи фінансового аналізу, що належать до групи неформалізованих. У чому полягає їх особливість?
Які вимоги повинна задовольняти коректно сформована система показників?
Назвіть головні принципи, яких необхідно додержувати при формуванні системи показників. Чи завжди можливе додержання всіх принципів?
У чому полягає сутність принципу розумного поєднання абсолютних і відносних показників?
Яким чином забезпечується додержання принципу неформальності при формуванні системи показників?
Назвіть завдання, які вирішуються за допомогою методу порівняння.
Чи може порівняння мати якісний характер?
Які фінансово-економічні показники використовуються як базові при проведенні порівняння?
Які результати дає порівняння фактичних даних із плановими показниками?
За яких умов досягається порівнянність показників?
23.На яких етапах аналізу фінансово-економічної діяльності суб'єкта господарювання використовуються аналітичні таблиці?
У чому відмінність аналітичних і статистичних таблиць?
Визначте сутність прийому деталізації. За якими критеріями вона може відбуватися?
В якому випадку найбільш доцільно застосовувати методи експертних оцінок? На чому вони грунтуються?
За яких умов метод мозкового штурму є найбільш ефективним?
У чому полягає сутність методу асоціацій та аналогій?
Охарактеризуйте класифікацію факторів, які впливають на функціонування соціально-економічних систем.
Що таке внутрішньовиробничі резерви? Чи мають вони стосунок до фінансового аналізу?
Наведіть у найбільш загальних рисах алгоритм здійснення фінансового аналізу.
Які види взаємозв'язків існують між економічними явищами?
Відтворіть математичну формулу моделі факторної системи.
Охарактеризуйте типи зв'язків, які досліджуються в процесі факторного аналізу.
У чому сутність прийомів елімінування? Які прийоми елімінування вам відомі?
За яких умов є доцільним використання балансового методу?
Розкрийте сутність прийому ланцюгових підстановок. За яких умов його застосування є найбільш доцільним?
Обгрунтуйте різницю між прийомами арифметичних і абсолютних різниць.
Різновидом якого способу є прийом відсоткових різниць?
Які особливості застосування логарифмічного методу?
Розкрийте основні особливості традиційних методів фінансово-економічної статистики. Чому вони дістали таку назву?
Які види середніх величин ви знаєте?
У чому різниця між простими і зваженими середніми величинами?
Охарактеризуйте середню величину, яка найбільше використовується у фінансовому аналізі.
Дайте визначення інтервальних і моментних економічних показників.
З якою метою використовується середня геометрична величина?
Охарактеризуйте переваги відносних величин над середніми.
Яка загальна методика отримання відносних величин?
Наведіть класифікацію відносних величин.
Дайте визначенні індексу. Яка мета застосування індексного методу у фінансовому аналізі?
Назвіть відомі вам класифікації індексів.
У чому сутність методу групування?
Яка формула використовується для визначення довжини інтервалу в групі при проведенні групування?
Скільки видів групувань використовуються у фінансовому аналізі? Дайте їх характеристику.
Сформулюйте головне правило групування.
Що таке ряди динаміки? Яку інформацію одержує фінансовий аналітик з їх допомогою?
Охарактеризуйте показники, що використовуються для повнішої характеристики змін і тенденцій у рядах динаміки.
Які основні правила складання системи динамічних рядів?
Перелічіть завдання, які вирішуються за допомогою індексного методу.
У чому полягає сутність кореляційного аналізу?
Який зв'язок називають кореляційним?
Який з різновидів кореляційного зв'язку найбільш широко застосовується у фінансовому аналізі?
В яких межах змінюється значення коефіцієнта кореляції?
В яких випадках кореляційний зв'язок вважається відсутнім, слабким, середньої тісноти, сильним?
Які показники використовуються для перевірки нормальності одновимірних розподілів за умови невеликих виборок?
Яке значення коефіцієнта асиметрії свідчить про симетричний зв'язок?
Про що свідчить значне додатне значення ексцесу?
Наведіть приклади операцій, що проводяться у випадку, якщо розподіл значень у виборці сильно відрізняється від нормального?
Що показує рівняння регресії? З якою метою регресія використовується у фінансовому аналізі?
У чому головна відмінність регресійного аналізу від кореляційного?
Який метод найчастіше застосовується для побудови рівняння регресії?
За якою методикою перевіряється значимість рівняння регресії?
Чи може регресійна модель вважається придатною для практичного використання, якщо похибка апроксимації становить 11 %?
Скільки етапів включає практична реалізація кореляційно-регресійного аналізу? Дайте їх стислу характеристику.
Які методи відносять до сучасних методів факторного аналізу? Які завдання вони вирішують?
З якою метою застосовується дисперсійний аналіз?
Наведіть класифікацію сукупностей, прийняту у фінансовому аналізі. За яким принципом вона побудована?
Охарактеризуйте комплекс методів, що використовується для кількісної обробки просторово-часових сукупностей.
Який з методів дає найбільш достовірну характеристику закономірного зв'язку, притаманного сукупності показників, що вивчаються?
Чому методи аналізу розвитку ситуацій набули широкого поширення лише з розвитком комп'ютерної техніки?
Перелічіть чинники, які підтверджують важливість застосування методів аналізу розвитку ситуацій у фінансовому аналізі.
У чому полягає сутність інформаційного моделювання?
Якими чинниками визначається об'єктивність імітаційного моделювання?
В яких ситуаціях може здійснюватися прийняття фінансово-управлінських рішень? Дайте їх стислу характеристику.
Який з підходів використовується фінансовим аналітиком для вибору варіанта дії в умовах ризику?
Які результати дає застосування методу лінійного програмування? У чому його сутність?
Який з варіантів аналізу чутливості найбільш поширений на практиці?
Назвіть положення, що визначають логіку методів оцінки ефективності фінансових операцій.
Наведіть приклад найпростішої фінансової операції.
У чому відмінність між обліковою і відсотковою ставками?
Розкрийте сутність процесів дисконтування і нарощування.
З яким видом дисконтування ми маємо справу, якщо як коефіцієнт дисконтування використовується облікова ставка?
Про що свідчить значення коефіцієнта дисконтування?
Які схеми дисконтного нарахування вам відомі?
У чому економічна сутність грошових потоків пренумерандо і постнумерандо?
Які головні задачі можуть розв'язуватись у процесі оцінки грошового потоку?
Що розуміють під терміном «ануїтет»?
Які ви знаєте підходи до визначення ануїтету? У чому їх відмінність?
Що показує мультиплікуючий множник для ануїтету?
100. В якому випадку ануїтет називають безстроковим? Яка методика його оцінки?
ТЕСТОВІ ЗАВДАННЯ
1. До неформалізованих методів фінансового аналізу належать:
а) середніх величин, групування, індексні; експертних оцінок, сценаріїв, психологічні, морфологічні, порівняння;
б) математичні, статистичні;
в) імітаційного моделювання, лінійного планування, ситуаційного аналізу, прогнозування;
г) дисконтування, нарощення, аналізу грошових потоків.
2. Дескриптивні моделі фінансового аналізу базуються на:
а) використанні даних математичного прогнозу;
б) результатах порівняння фактичних результатів діяльності підприємств з очікуваними;
в) оцінці впливу окремих факторів та їх комбінацій;
г) даних регресійного аналізу;
д) використанні інформації фінансової звітності.
3. Модель товарного балансу підприємства належить до:
а) мультиплікативних моделей;
б) нормативних моделей;
в) адитивних моделей;
г) предикативних моделей;
д) стохастичних моделей факторного аналізу.
4. Принцип оглядовості передбачає:
а) максимальний ступінь аналітичності системи;
б) вилучення із сукупності показників зі значними корелятивними зв'язками;
в) наявність оптимального для підприємства набору показників;
г) існування в системі одиничних і узагальнюючих показників.
5. Методи експертних оцінок належать до класу:
а) статистичних;
б) математичних; в)евристичних;
г) порівняльних;
д) формалізованих.
6. Сутність дельфійського методу полягає у:
а) систематизованому огляді всіх можливих варіантів розвитку окремих елементів досліджуваної системи, побудованих на повних і строгих класифікаціях об'єктів і явищ, їх властивостей і параметрів;
б) виникненні нових ідей та пропозицій на основі зіставлення з іншими більш-менш аналогічними об'єктами;
в) послідовному індивідуальному анонімному опитуванні експертів;
г) якісній характеристиці досліджуваного об'єкта або явища при різних поєднаннях раніше визначених умов.
