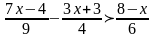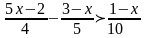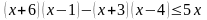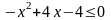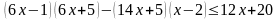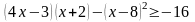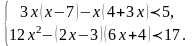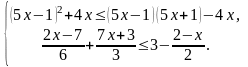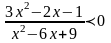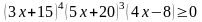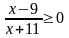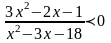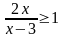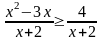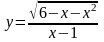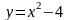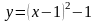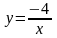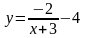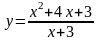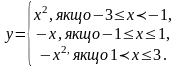Нерівності та їх системи
Розв’язати лінійні нерівності:
.
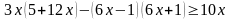
Розв’язати квадратні нерівності:
Розв’язати системи нерівностей:
.
Розв’язати нерівності, що зводяться до системи нерівностей:
.
.
.
.
Розв’язати нерівності методом інтервалів:
Функції та її властивості
Знайти область визначення функції:
Побудувати графік функції та описати її властивості
Арифметична та геометрична прогресії.
Знайдіть суму членів арифметичної прогресії , якщо
,
,
.Знайдіть суму членів арифметичної прогресії , якщо
,
,
.В арифметичній прогресії
,
.
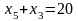Знайдіть суму перших дев’яти членів.
В арифметичній прогресії
,
.
Знайдіть суму перших десяти членів.
Визначить перший член і різницю арифметичної прогресії, якщо
,
.Визначить перший член і різницю арифметичної прогресії, якщо
,
.Знайдіть перший та п’ятий члени арифметичної прогресії, якщо різниця її дорівнює 7, а сума шести її перших членів дорівнює 159.
Знайдіть перший та шостий члени арифметичної прогресії, якщо різниця її дорівнює 9, а сума восьми її перших членів дорівнює 180.
Знайдіть восьмий член і знаменник геометричної прогресії, якщо
,
.Знайдіть сьомий член і знаменник геометричної прогресії, якщо
,
.Знайдіть перший та п’ятий члени геометричної прогресії, якщо її знаменник дорівнює 3, а сума шести її перших членів дорівнює 1820.
Знайдіть перший та шостий члени геометричної прогресії, якщо її дорівнює знаменник 2, а сума восьми її перших членів дорівнює 765.
Перший член геометричної прогресії дорівнює 2, а третій дорівнює 18. Скільки перших членів треба взяти, щоб їх сума дорівнювала 242.
Перший член геометричної прогресії дорівнює 3, а п’ятий дорівнює 48. Скільки перших членів треба взяти, щоб їх сума дорівнювала 381.
Знайдіть суму нескінченно спадної геометричної прогресії, в якій четвертий член дорівнює
,
а знаменник дорівнює
.Знайдіть суму нескінченно спадної геометричної прогресії, в якій четвертий член дорівнює
,
а знаменник дорівнює
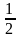.Знайдіть четвертий член нескінченно спадної геометричної прогресії, сума якої дорівнює
,
а перший член дорівнює
.Знайдіть четвертий член нескінченно спадної геометричної прогресії, сума якої дорівнює48, а перший член дорівнює 24.
Три числа, що дають у сумі 21, становлять геометричну прогресію. Якщо до них відповідно додати 2, 3, 1, то утворені числа становитимуть арифметичну прогресію. Знайти ці числа.
Три числа, що дають у сумі 21, становлять геометричну прогресію. Якщо від них відповідно відняти 1, 1, 4, то утворені числа становитимуть арифметичну прогресію. Знайти ці числа.
Три числа, що дають у сумі 27, становлять арифметичну прогресію. Якщо від них відповідно відняти 1, 3, 2, то утворені числа становитимуть геометричну прогресію. Знайти ці числа.
Три числа, що дають у сумі 12, становлять арифметичну прогресію. Якщо від них відповідно відняти 1, 2, 11, то утворені числа становитимуть геометричну прогресію. Знайти ці числа.