12. Задачі до теми „Інтеграл” .
12.1.
Обчислити інтеграли, застосувавши
таблицю інтегралів, спрощення
підинтегральної функції і найпростіші
правила інтегрування:
12.2.
Обчислити інтеграли методом заміни
змінної (=інтегрування підстановкою)
:
12.3. Обчислити інтеграли методом інтегрування частинами:
12.4. Обчислити інтеграли, застосувавши підходящий спосіб.
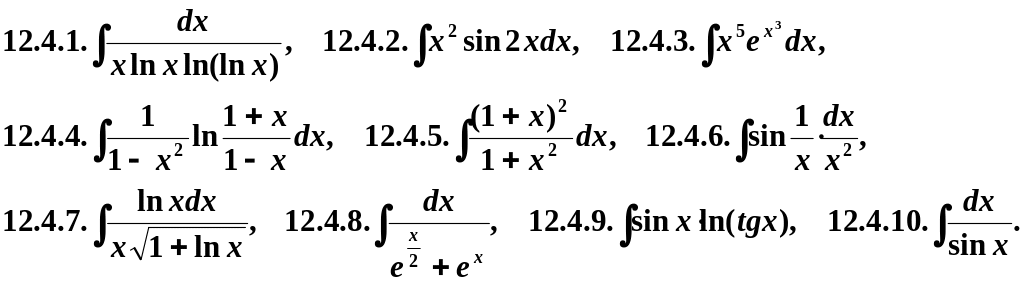
13. Задачі до теми „Диференціальні рівняння” .
13.1. Розв’язати диференціальні рівняння з відокремленими змінними; побудувати графіки функцій, що є їх розв’язками:
13.1.
1)
,
13.1. 2)
,
13.1.
3)
,
13.1.
4)
, 13.5. 3)
,
13.1.
6)
,
13.1. 7)
,
13.1. 8)
.
13.2. Розв’язати однорідні диференціальні рівняння; побудувати графіки функцій, що є їх розв’язками:
13.2.
1)
,
13.2. 2)
,
13.2.
3)
,
13.2. 4)
,
13.2. 5)
.
13.3. Розв’язати лінійні диференціальні рівняння; побудувати графіки функцій, що є їх розв’язками:
13.3.
1)
, 13.3. 2)
,
13.3. 3)
,
13.3.
4)
,
13.3. 5)
,
13.3.
6)
.
13.4.
Розв’язати диференціальні рівняння,
розв’язавши їх спочатку відносно
;
побудувати графіки функцій, що є їх
розв’язками:
13.4.
1)
,
13.4. 2)
,
13.4. 3)
,
13.4.
4)
, 13.4. 5)
.
13.5. Розв’язати диференціальні рівняння підходящим способом; побудувати графіки функцій, що є їх розв’язками:
13.5.
1)
,
13.5. 2)
,
13.5. 3)
,
13.5.
4)
,
13.5. 5)
,
13.5. 6)
,
13.5.
7)
,
13.5. 8)
.
14. Задачі до теми „Функції багатьох змінних” .
14.1. Знайти значення параметрів функціональних залежностей за даними спостережень методом найменших квадратів, утворивши функцію сумарної квадратичної нев’язки і застосувавши узагальнену теорему Ферма; розв’язання супроводити графічною ілюстрацією:
14.1.1)
;
14.1.2)
;
14.1.3)
.
14.2.
Побудувати декілька ліній рівня (
)
функції
(попередньо виділивши повні квадрати
відповідних виразах по кожній змінній);
за побудованими лініями рівня виконати
зображення просторової поверхні
:
14.2.1)
;
14.2.2)
;
14.2.3)
.
14.3.
Розв’язавши рівняння відносно
і побудувавши декілька ліній рівня (
)
утвореної функції
,
відновити графік (просторовий) відповідної
поверхні:
14.3.1)
;
14.3.2)
;
14.3.3)
.
14.4.
Здійснити 3 кроки методу
найскорішого спуску
для функції
.
Кожний крок методу складається з дій:
-
обчислити значення координат
вектора-градієнта
функції
в точці
;
-
скласти рівняння прямої, що проходить
через точку
і має направляючий вектор
:
;
підставити координати біжучої точки
у функцію
,
утворивши тим самим функцію однієї
змінної
;знайти точку мінімуму
функції
за допомогою класичної теореми Ферма;обчислити координати точки
.
На першому кроці за точку взяти початок координат; на кожному наступному – обчислену на попередньому кроці точку .
Література
(Рекомендована міністерством освіти і науки) Основна література
Барковський В.В., Барковська Н.В. Математика для економістів:Вища математика:Навч. Посібн..-К.:НАУ,1997,1999.
Валєєв К.Г.,Джалладова І.А. Навч. Посібник. У 2-х ч.-К.:КНЕУ, 2001.
Вища математика: Навч.-метод. Посібн. Для самост. Вивч. Дисципліни / К.Г.Валєєв, І.А.Джалладова, О.І.Лютий, О.І.Макаренко, В.Г.Овсієнко.-К.:КНЕУ, 1999.
Высшая математика для экономистов: Учеб.пособие/ Под ред.Н.Ш. Кремера.- Банки и биржи, ЮНИТИ, 1997, 2000.
Неміш В.М., Процик А.І., Березька К.М. Вища математика (практикум): Навч.посібник.- Тернопіль: Економічна думка, 2001.
Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс. Збірник задач та вправ.- Харків: Рубікон,1999.
Ефимов Н.В. Краткий курс аналитической геометрии.- М.: Физматгиз, 1973.
Привалов И.И. Аналитическая геометрия.- М.: Наука, 1966.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.- М.:Наука, 1984.
Клетеник Д.В. Сборник задач по аналитической геометрии.- М.: Наука, 1986.
Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии.- М.: Наука, 1970.
Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1, Т.2.- М.: Наука, 1976.
Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов.- М.: Наука, 1971.
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление.- М.: Наука, 1984.
Берман Г.Н. Сборник задач по курсу математического анализа.- М.:Наука, 1985.
Задачи и упражнения по математическому анализу для втузов. Под ред. Б.П. Демидовича.- М.: Наука, 1978.
Дубровник В.П., Юрик І.І. Вища математика: Навч.посібник.- К.: Вища школа, 1993, 648с.
Бугров Я.С., Никольский С.М.Элементы линейной алгебры и аналитической геометрии.- М.: Наука, 1983.
Ильин В.А., Позняк Е.Г. Линейная алгебра.- М.: Наука, 1981.
Икрамов Х.Д. Задачник по линейной алгебре.- М.: Физматгиз, 1985.